Phân tích hồi quy tuyến tính là một bước quan trọng sau khi thực hiện phân tích tương quan trong quy trình kiểm định SPSS. Sau đây, Xulysolieu sẽ hướng dẫn từng bước thực hiện hồi quy tuyến tính bằng SPSS, đưa ra diễn giải cụ thể và cách báo cáo kết quả một cách dễ hiểu.

1. Tổng quan về hồi quy tuyến tính trong SPSS

Trong nghiên cứu, chúng ta thường cần kiểm tra các giả thuyết về mối quan hệ giữa các biến. Nếu chỉ có một biến độc lập, ta sử dụng mô hình hồi quy tuyến tính đơn (SLR). Ngược lại, nếu có hai hoặc nhiều biến độc lập, ta dùng hồi quy tuyến tính đa biến (MLR). MLR là một phiên bản mở rộng của SLR, cho phép phân tích mối tương quan giữa một biến phụ thuộc và nhiều biến độc lập cùng một lúc.

Bài viết này tập trung vào hồi quy tuyến tính đa biến (MLR), mặc dù các nguyên tắc cơ bản cũng áp dụng cho hồi quy tuyến tính đơn (SLR). Dưới đây là phương trình cho cả hai loại:

• Phương trình hồi quy tuyến tính đơn (SLR): Y = β₀ + β₁X + e
• Phương trình hồi quy tuyến tính đa biến (MLR): Y = β₀ + β₁X₁ + β₂X₂ + … + βₙXₙ + e

Trong đó, mục tiêu là xác định các hệ số β₀ và β₁ sao cho mô hình phù hợp nhất với dữ liệu. Các thành phần của phương trình được định nghĩa như sau:

• Y: biến phụ thuộc, biến chịu tác động từ các biến khác.
• X, X₁, X₂, Xₙ: (các) biến độc lập, biến ảnh hưởng đến biến khác.
• β₀: hằng số hồi quy, còn gọi là hệ số chặn.
  • Hằng số hồi quy (β₀) là giá trị của biến phụ thuộc Y khi tất cả các biến độc lập X đều bằng 0. Điều này thể hiện giá trị cơ sở của Y khi không có tác động từ bất kỳ biến độc lập nào.
  • Trên đồ thị hai chiều (Oxy), β₀ là giao điểm của đường hồi quy với trục Oy. Nó cho biết giá trị ban đầu của biến phụ thuộc trước khi có bất kỳ ảnh hưởng nào từ các biến độc lập.
• β₁, β₂, βₙ: hệ số hồi quy, hay còn được gọi là hệ số góc.
  • Hệ số hồi quy (βᵢ) (với i = 1, 2, …, n) cho biết mức độ thay đổi của biến phụ thuộc Y ứng với mỗi đơn vị thay đổi của biến độc lập Xᵢ. Nói cách khác, βᵢ thể hiện sự thay đổi của Y khi Xᵢ tăng hoặc giảm một đơn vị.
  • Trong đồ thị hai chiều, hệ số hồi quy (βᵢ) là độ dốc của đường hồi quy liên quan đến biến Xᵢ. Điều này giúp ta hiểu mức độ ảnh hưởng của từng biến độc lập lên biến phụ thuộc.
• e: sai số, thể hiện sai lệch giữa giá trị dự đoán của mô hình và giá trị thực tế. Sai số càng lớn, khả năng dự đoán của mô hình càng kém chính xác.
  • Sai số trong hồi quy tổng thể: Đây là sự khác biệt giữa giá trị dự đoán và giá trị thực tế trên toàn bộ dữ liệu, phản ánh khả năng dự đoán của mô hình trên tất cả các quan sát.
  • Sai số phần dư trong hồi quy mẫu: Đây là sự khác biệt giữa giá trị dự đoán và giá trị thực tế trên từng quan sát cụ thể trong mẫu dữ liệu, bao gồm hai thành phần:
    • Các biến độc lập ngoài mô hình: Ảnh hưởng của các biến không được đưa vào mô hình hồi quy.
    • Các sai số ngẫu nhiên: Sai số không thể dự đoán được, phụ thuộc vào yếu tố ngẫu nhiên và các yếu tố không xác định.

Trong thống kê, chúng ta thường muốn đánh giá thông tin về tổng thể, nhưng vì tổng thể thường quá lớn để thu thập toàn bộ dữ liệu, chúng ta sử dụng thông tin từ mẫu nghiên cứu để ước lượng hoặc kiểm định thông tin của tổng thể.

Trong hồi quy tuyến tính, các hệ số hồi quy tổng thể như β₁, β₂, βₙ hay hằng số hồi quy β₀ là những tham số chúng ta quan tâm. Chúng không thể đo trực tiếp được, vì vậy, chúng ta sử dụng tham số tương ứng từ mẫu để ước lượng và từ đó suy diễn ra thông tin về tổng thể.

Phương trình hồi quy tuyến tính trên mẫu nghiên cứu có dạng:

Y = B₀ + B₁X₁ + B₂X₂ + … + BₙXₙ + ε

Trong đó:

• Y: biến phụ thuộc
• X, X₁, X₂, Xₙ: biến độc lập
• B₀: hằng số hồi quy
• B₁, B₂, Bₙ: hệ số hồi quy
• ε: phần dư

Các phân tích hồi quy tiếp theo sẽ tập trung vào dữ liệu mẫu, sử dụng thuật ngữ “phần dư” thay vì “sai số.” Khi hai hoặc nhiều biến có tương quan, hồi quy tuyến tính có thể phân tích mối quan hệ nhân quả, với một biến là biến phụ thuộc (Y) và các biến còn lại là biến độc lập (X).

2. Tìm hiểu về phương pháp ước lượng OLS

Một phương pháp phổ biến để ước lượng hồi quy tuyến tính là phương pháp bình phương tối thiểu OLS (Ordinary Least Squares). Mục tiêu của OLS là giảm thiểu biến thiên của phần dư trong phép hồi quy.

Về mặt trực quan, đường hồi quy OLS là đường thẳng đi qua đám mây điểm dữ liệu trên mặt phẳng Oxy. Đường này được xác định sao cho tổng khoảng cách từ mỗi điểm dữ liệu đến đường hồi quy (biểu thị bằng trị tuyệt đối của ε) là nhỏ nhất.

Trong tổng thể, sai số (e) biểu thị sự chênh lệch giữa giá trị dự đoán của mô hình hồi quy và giá trị thực tế. Sai số này phản ánh mức độ không hoàn hảo của mô hình trong việc dự đoán.

Trong mẫu nghiên cứu, sai số được gọi là phần dư (ε), là sự khác biệt giữa giá trị dự đoán và giá trị thực tế trên từng quan sát cụ thể. Biến thiên của phần dư được tính bằng tổng bình phương của tất cả các phần dư.

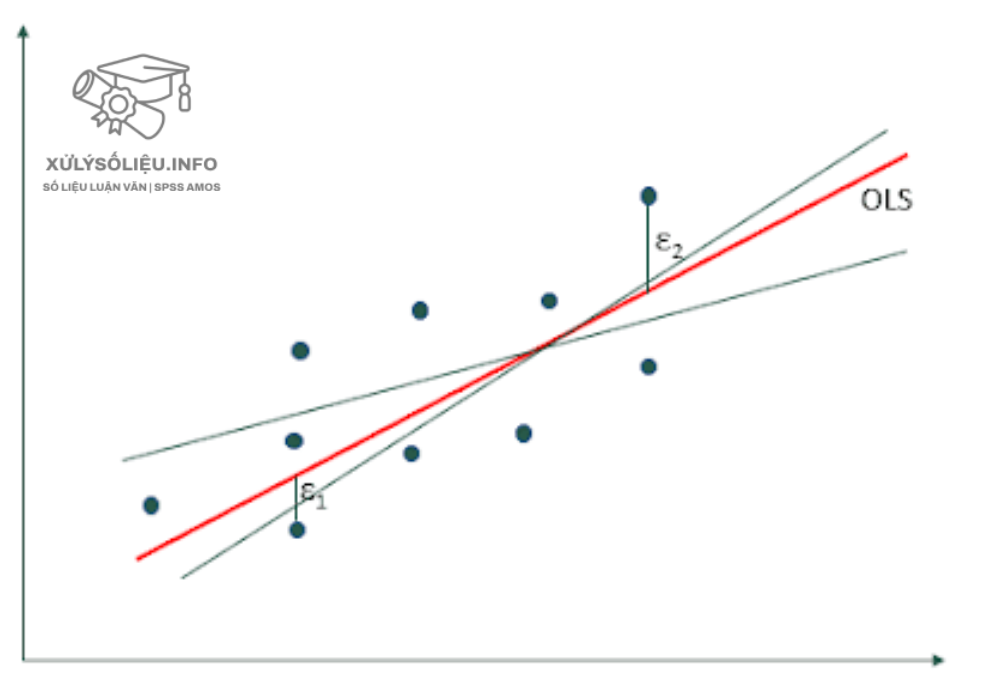
Ước lượng hồi quy tuyến tính bằng OLS trong SPSS

Đồ thị phân tán (scatter plot) biểu diễn mối quan hệ giữa các biến độc lập và biến phụ thuộc. Các điểm dữ liệu phân tán trên đồ thị, tạo thành một đám mây điểm, thể hiện xu hướng chung của dữ liệu.

Trong hồi quy tuyến tính, ta cố gắng tìm đường thẳng mô tả sát nhất xu hướng này. Có nhiều đường hồi quy có thể đi qua đám mây điểm dữ liệu. Phương pháp bình phương tối thiểu OLS sẽ xác định đường thẳng tối ưu, dựa trên nguyên tắc tối thiểu hóa khoảng cách từ các điểm dữ liệu đến đường hồi quy. Trong hình trên, đường màu đỏ là đường hồi quy OLS.

3. Hướng dẫn từng bước phân tích hồi quy tuyến tính trong SPSS

Đảm bảo các giả định hồi quy

Hồi quy tuyến tính là một công cụ phân tích mạnh mẽ, nhưng để đảm bảo tính chính xác, cần kiểm tra các giả định trước khi áp dụng:

Việc kiểm tra giả định giúp đảm bảo rằng dữ liệu phù hợp với mô hình hồi quy, từ đó mang lại kết quả chính xác và có ý nghĩa thống kê. Bỏ qua bước này có thể dẫn đến những sai lệch nghiêm trọng.

(1) Biến phụ thuộc là biến liên tục: Biến phụ thuộc (Y) phải được đo lường trên thang đo liên tục (ví dụ: điểm thi, thu nhập).

(2) Biến độc lập là biến liên tục: Biến độc lập (X) cũng phải được đo lường trên thang đo liên tục (ví dụ: số giờ học, chi phí quảng cáo).

(3) Quan hệ tuyến tính: Mối quan hệ giữa biến phụ thuộc và biến độc lập phải là tuyến tính; tức là, sự thay đổi ở biến độc lập dẫn đến sự thay đổi tương ứng ở biến phụ thuộc theo một tỷ lệ gần như không đổi.

(4) Không có giá trị ngoại lệ: Dữ liệu không được chứa các điểm dữ liệu quá khác biệt so với phần còn lại.

(5) Tính độc lập: Các sai số phải độc lập với nhau, nghĩa là sai số ở một quan sát không ảnh hưởng đến sai số ở các quan sát khác.

(6) Phương sai đồng nhất: Phương sai của sai số phải không đổi ở tất cả các mức giá trị của biến độc lập.

(7) Phân phối chuẩn của sai số: Các sai số phải tuân theo phân phối chuẩn với giá trị trung bình bằng 0.

Thực hiện hồi quy tuyến tính trong SPSS: Chi tiết

Ví dụ: Một sinh viên muốn xác định mối quan hệ giữa “Các yếu tố liên quan đến sản phẩm sữa Fami” (biến độc lập) và “Quyết định chấp nhận sản phẩm Fami” (biến phụ thuộc).

• Tạo các biến để nhập dữ liệu: Các yếu tố liên quan đến sản phẩm sữa (biến độc lập) và Quyết định chấp nhận sản phẩm sữa (biến phụ thuộc).
• Tạo biến số thứ ba (case number): Biến này (tùy chọn) lưu trữ số thứ tự của mỗi trường hợp, hữu ích khi cần loại bỏ các trường hợp ngoại lệ.

Để thực hiện phân tích hồi quy tuyến tính bội theo phương pháp OLS, thực hiện các bước sau:

• Bước 1: Trong SPSS, chọn Analyze > Regression > Linear.

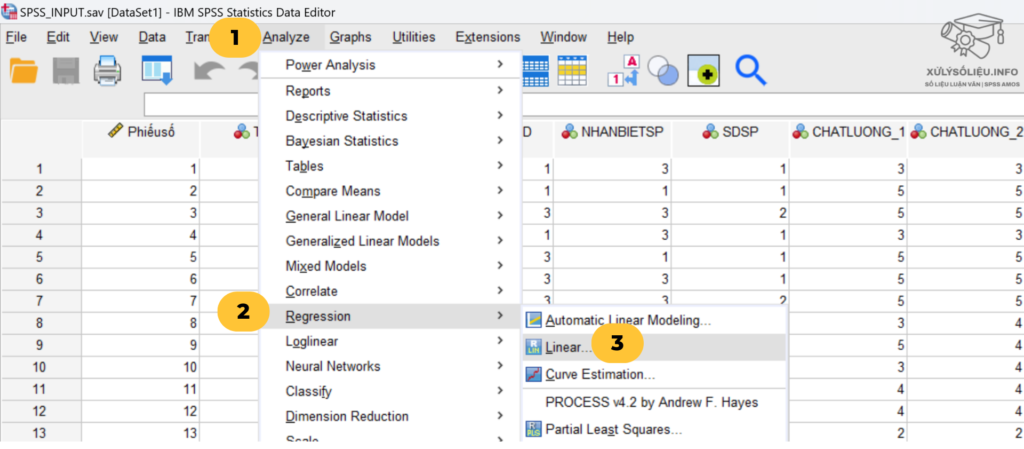Nhấp vào Analyze > Regression > Linear

Hộp thoại Linear Regression sẽ xuất hiện.

• Bước 2: Chuyển các biến độc lập vào hộp Independent(s) và biến phụ thuộc vào hộp Dependent.

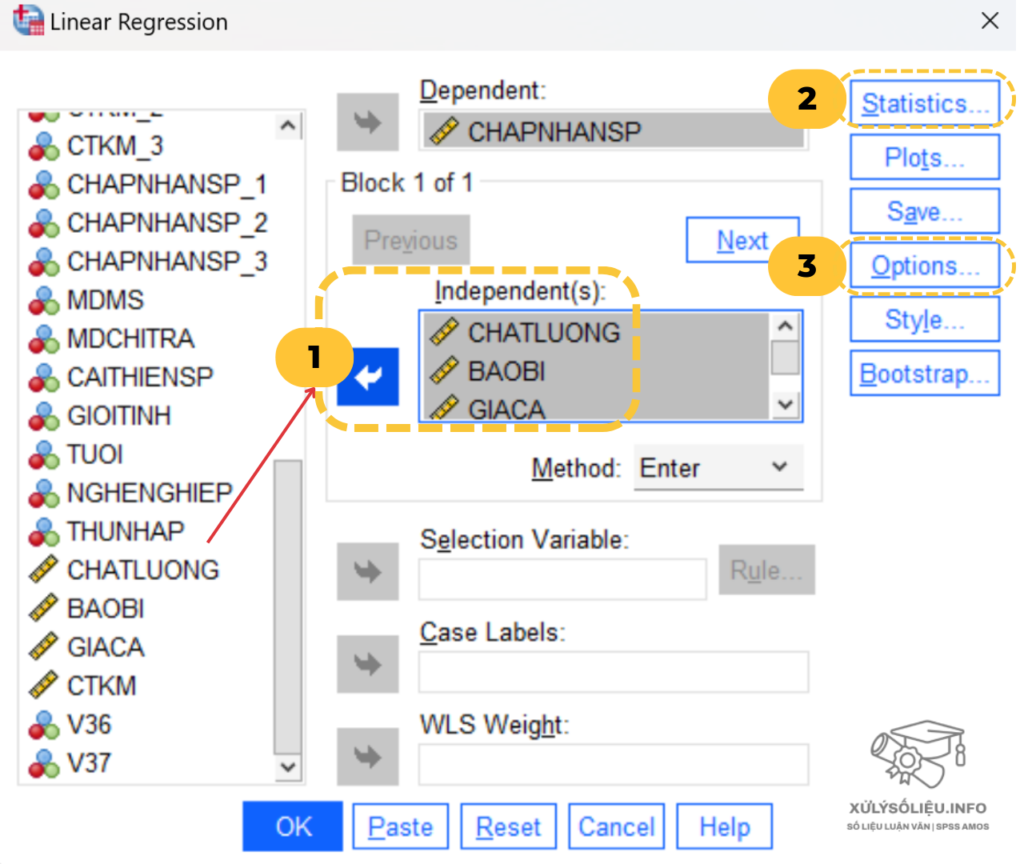
• Bước 3: Kiểm tra các giả định về giá trị ngoại lệ, tính độc lập, phương sai đồng nhất và phân phối chuẩn của sai số. Trong hộp Statistics, tích chọn các mục như trong hình minh họa và chọn Continue.

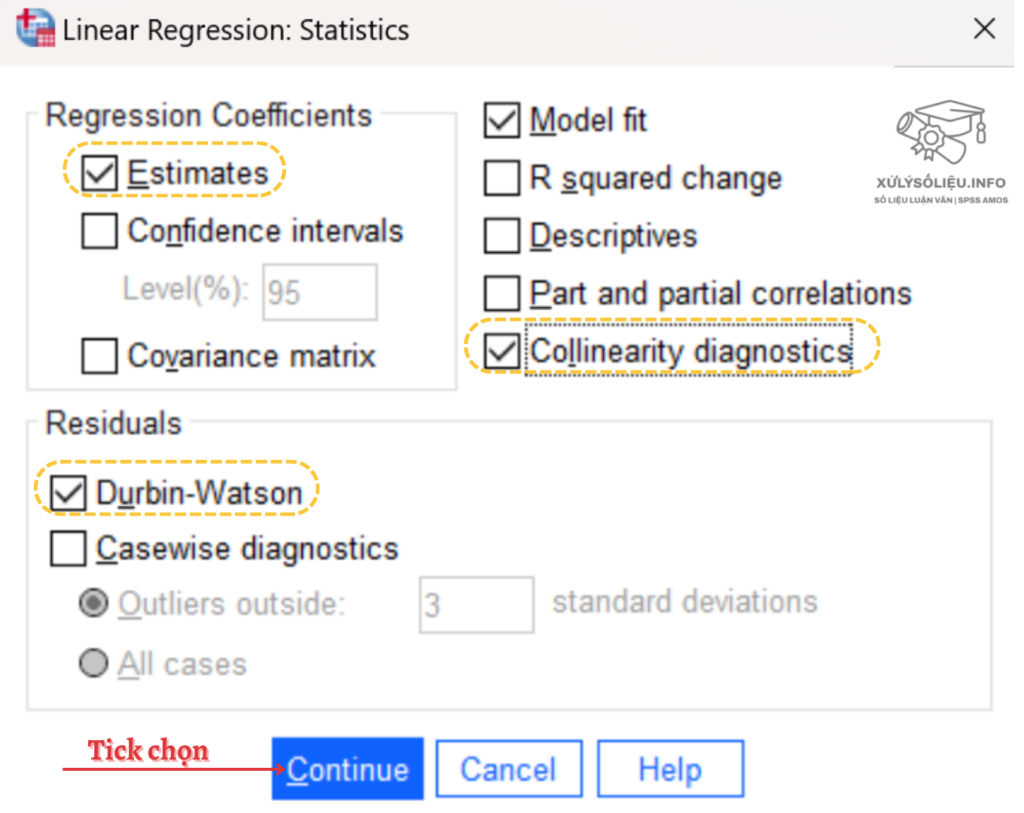
Tiếp tục chọn Plots, tích chọn Histogram và Normal probability plot, kéo thả biến ZRESID vào ô Y và ZPRED vào ô X như hình dưới, sau đó chọn Continue.

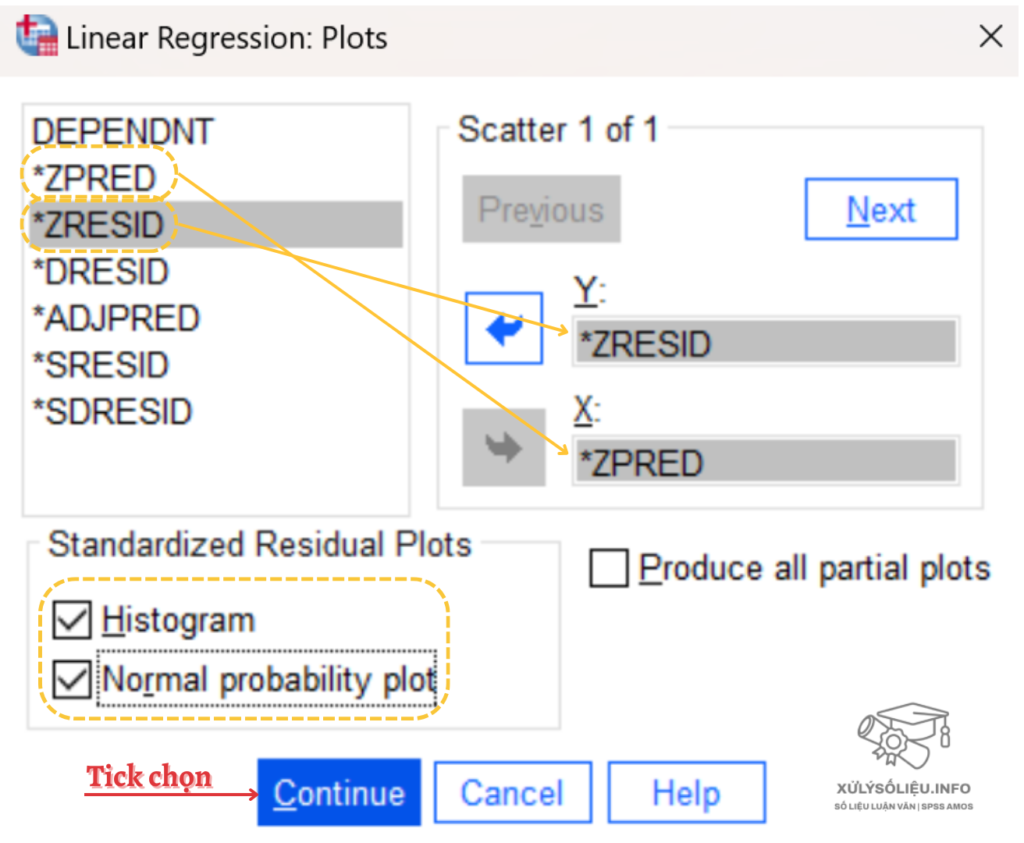
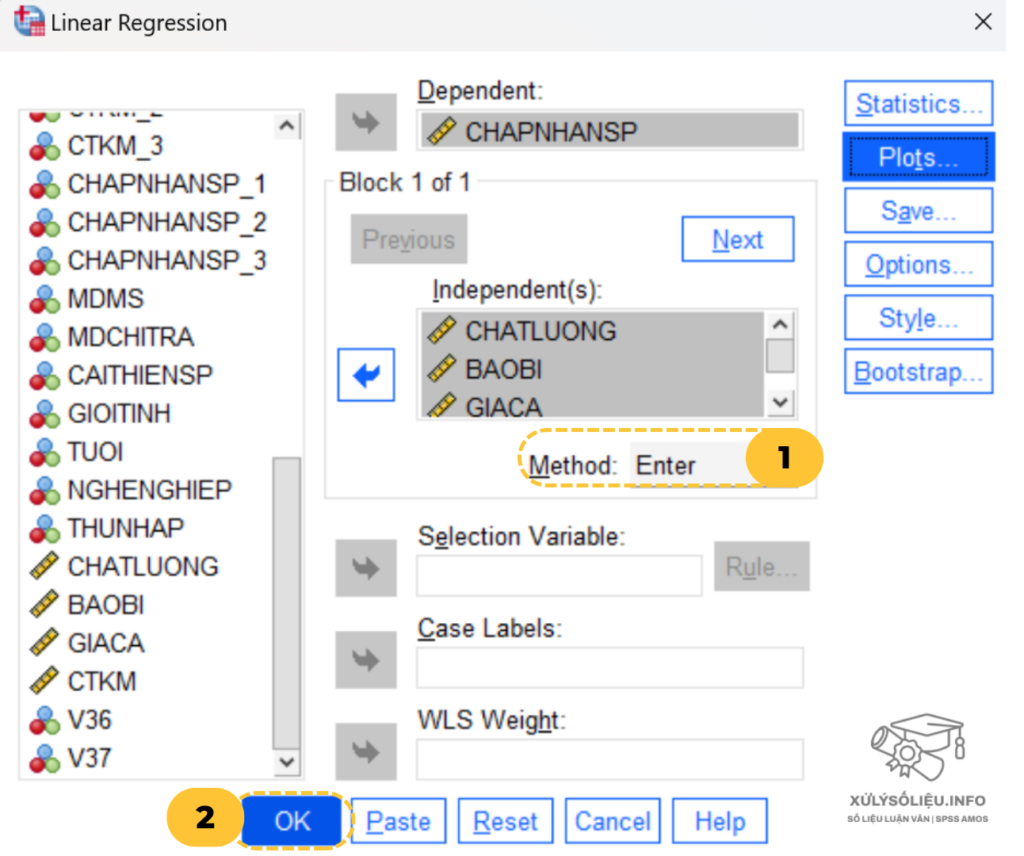
• Bước 4: Quay lại giao diện ban đầu, chọn phương pháp đưa biến vào mô hình hồi quy (trong phần Method). Chọn Enter để đưa tất cả các biến vào mô hình cùng một lúc. Nhấp vào OK để chạy hồi quy.

4. Giải thích kết quả hồi quy tuyến tính trong SPSS

SPSS sẽ tạo ra nhiều bảng và biểu đồ. Chúng ta sẽ tập trung vào 3 bảng chính (ANOVA, Model Summary, Coefficients) và 3 biểu đồ (Histogram, Normal P-P Plot, Scatter Plot) để hiểu kết quả (giả sử không có giả định nào bị vi phạm).

Bảng Model Summary

Trong phân tích hồi quy, sự phân tán của các điểm dữ liệu là điều không thể tránh khỏi. Để đánh giá mức độ phù hợp của mô hình, chúng ta cần tính toán các chỉ số như sai số chuẩn, hệ số xác định và kiểm tra giả thuyết về các hệ số hồi quy.

Hệ số xác định R² (R square) là một thước đo mức độ phù hợp. R² càng cao, mô hình càng phù hợp.

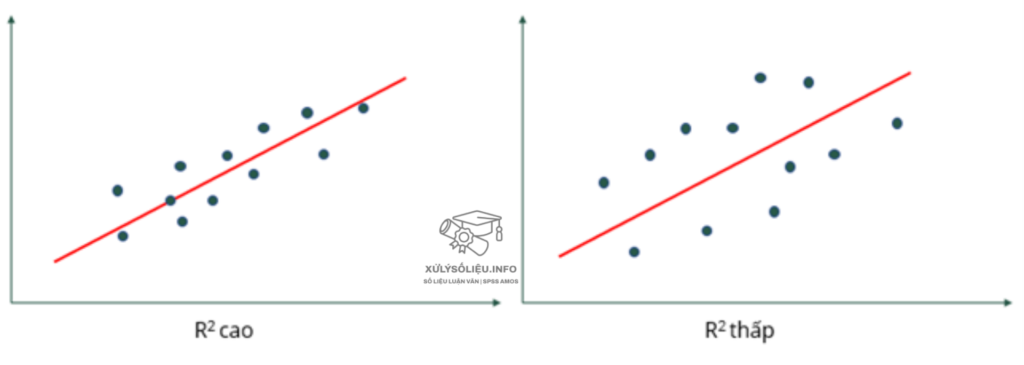Khác nhau giữa giá trị R2 cao và thấp

Bảng Model Summary chứa các chỉ số để đánh giá sự phù hợp của mô hình:

• Hệ số Durbin-Watson (DW): Đánh giá hiện tượng tự tương quan chuỗi bậc nhất. DW có giá trị từ 0 đến 4:
  • DW ≈ 2: Các phần dư không có tương quan chuỗi bậc nhất.
  • DW ≈ 0: Phần dư có tương quan thuận.
  • DW ≈ 4: Phần dư có tương quan nghịch.
• Hệ số tương quan Pearson (R): Đo lường mức độ tương quan tuyến tính giữa Y và X (giá trị từ 0 đến 1):
  • R = 0: Biến Y và X không tương quan.
  • 0 0.05: Chấp nhận giả thuyết H0, nghĩa là biến Xi không tác động lên biến phụ thuộc.

  Trong phân tích hồi quy, thường có hai loại hệ số hồi quy: hệ số chưa chuẩn hóa (B) và hệ số đã chuẩn hóa (Beta). Chúng ta sẽ sử dụng hệ số đã chuẩn hóa để phản ánh ý nghĩa thực tiễn của các biến. -Hệ số hồi quy (B hoặc Beta) có dấu âm: biến độc lập tác động ngược chiều lên biến phụ thuộc. -Hệ số B hoặc Beta có dấu dương: biến độc lập tác động cùng chiều lên biến phụ thuộc. Khi xem xét mức độ ảnh hưởng của các biến độc lập, giá trị tuyệt đối của hệ số Beta càng lớn, biến độc lập tác động càng mạnh.

  Nếu một biến độc lập không có ý nghĩa thống kê, chúng ta có thể kết luận rắng biến đó không có ảnh hưởng đáng kể mà không cần loại bỏ biến và phân tích lại. 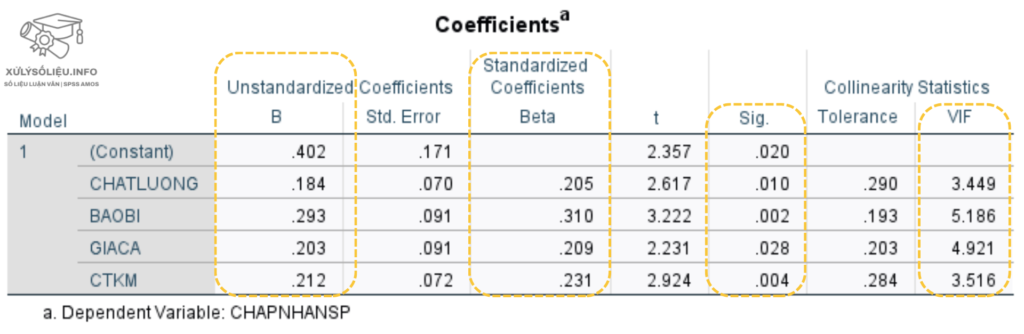Kết quả bảng Coefficients

  Các biến độc lập gồm CHATLUONG, GIACA, BAOBI, CTKM đều có sig kiểm định t nhỏ hơn 0.05 và hệ số hồi quy dương.

  Kết luận:

  • Chất lượng sản phẩm (CHATLUONG) tác động đến sự hài lòng (Chấp nhận)
  • Giá cả (GIACA) tác động đến Quyết định chấp nhận sản phẩm (Chấp nhận)
  • Bao bì (BAOBI) tác động đến Quyết định chấp nhận sản phẩm (Chấp nhận)
  • Chương trình khuyến mãi (CTKM) tác động đến Quyết định chấp nhận sản phẩm (Chấp nhận)

  Phương trình hồi quy tuyến tính:

  • Dạng chuẩn hóa: Y = 0.205*CHATLUONG + 0.310*BAOBI + 0.209*GIACA + 0.231*CTKM + ε
  • Dạng chưa chuẩn hóa: Y= 0.402 + 0.184*CHATLUONG + 0.293*BAOBI + 0.203*GIACA + 0.212*CTKM + ε

  Những lưu ý khi viết phương trình hồi quy:

  • Không đưa biến độc lập không có ý nghĩa thống kê vào.
  • Nếu hệ số hồi quy âm, viết dấu trừ trước.
  • Xác định biến độc lập tác động mạnh nhất dựa vào giá trị tuyệt đối.
  • Luôn có phần dư ε.

  Hệ số phóng đại phương sai (VIF): đánh giá hiện tượng đa cộng tuyến. VIF càng thấp, khả năng xảy ra đa cộng tuyến càng nhỏ. Nên cố gắng giữ VIF ở mức thấp(VIF < 2: cần cẩn thận)

  Dữ liệu không vi phạm giả định đa cộng tuyến (VIF < 10).

  Biểu đồ tần số phần dư chuẩn hóa (Histogram)

  Mục đích: Xác định phân bố của phần dư.

  • Phân bố chuẩn: Phần dư phân bố đều đặn quanh đường 0, không có hiện tượng skewness hoặc kurtosis.
  • Phân bố khác chuẩn: Cần xem xét kĩ lưỡng trước khi đưa ra kết luận Lưu ý: Nên sử dụng biểu đồ mật độ thay cho biểu đồ tần số khi có nhiều dữ liệu. Phần dư có thể không tuân theo phân phối chuẩn vì những lý do như: sử dụng sai mô hình, phương sai không phải là hằng số, số lượng các phần dư không đủ nhiều để phân tích…

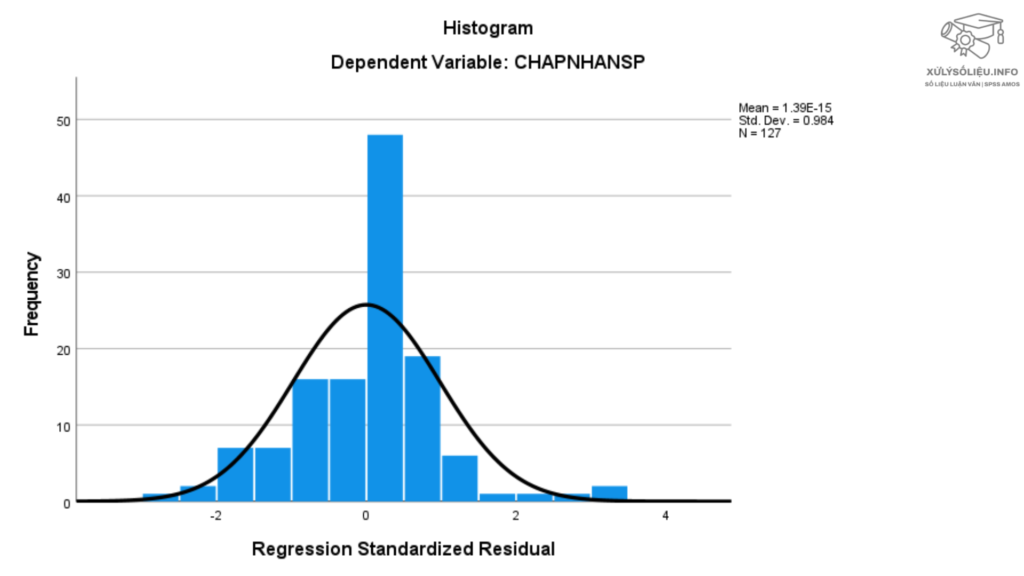
    Biểu đồ tần số phần dư chuẩn hóa Histogram Trong ảnh trên, phân phối phần dư xấp xỉ chuẩn (Mean=0, độ lệch chuẩn ≈ 1 ).

  Biểu đồ phần dư chuẩn hóa (Normal P-P Plot)

  Mục đích: So sánh phân bố thực tế của phần dư với phân bố chuẩn.

  • Điểm dữ liệu nằm gần đường chéo: Phân bố thực tế gần giống phân bố chuẩn.
  • Điểm dữ liệu lệch khỏi đường chéo: Phân bố thực tế khác phân bố chuẩn.

  Lưu ý: Cần xem xét kết hợp với các biện pháp thống kê khác để đưa ra kết luận chính xác. 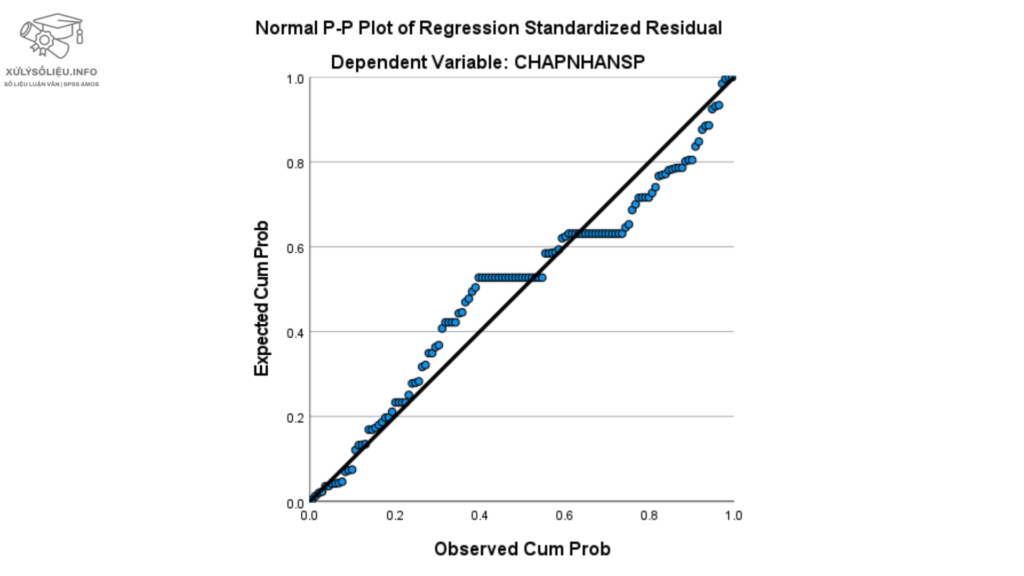Biểu đồ phần dư chuẩn hóa Normal P-P Plot

  Phần dư có phân phối xấp xỉ chuẩn

  Biểu đồ Scatter Plot giả định liên hệ tuyến tính

  Mục đích: Kiểm tra giả định về mối quan hệ tuyến tính giữa biến phụ thuộc (Y) và biến độc lập (X).

  • Mối quan hệ tuyến tính: Điểm dữ liệu xếp xấp xỉ theo đường thẳng
  • Mối quan hệ phi tuyến tính: Điểm dữ liệu không xếp xấp xỉ theo đường thẳng Lưu ý: Cần xem xét kỹ lưỡng hình dạng của biểu đồ và sử dụng các phương pháp thống kê khác để xác nhận giả định tuyến tính.

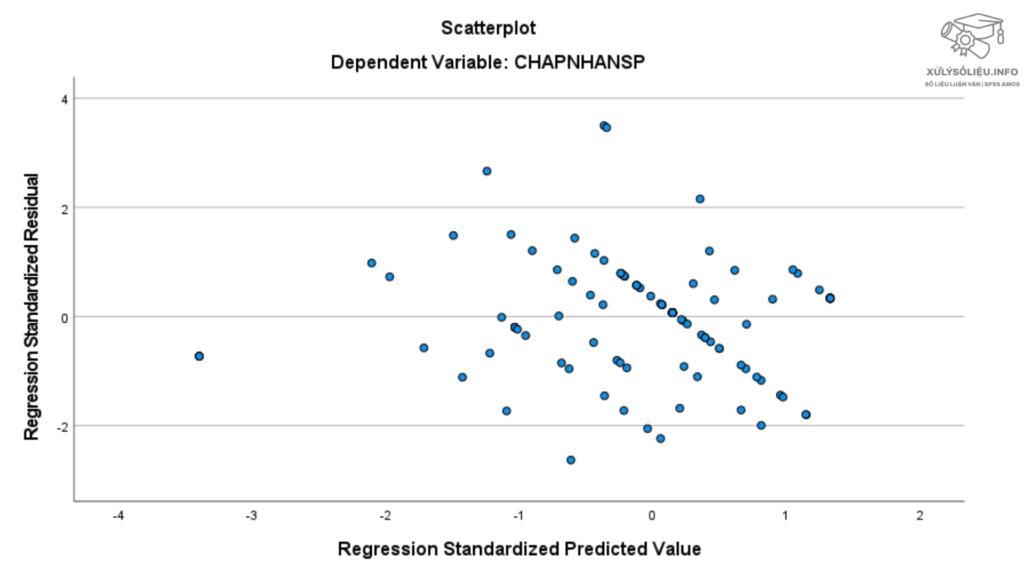  Biểu đồ Scatter Plot giả định liên hệ tuyến tính Giả định quan hệ tuyến tính không bị vi phạm.

  Nếu chỉ số R2 quá thấp hoặc xảy ra hiện tượng đa cộng tuyến, hãy tham khảo ngay dịch vụ chạy SPSS của xulysolieu.info .