Trong phân tích hồi quy, một công việc quan trọng không chỉ là ước lượng mối quan hệ giữa các biến mà còn là đánh giá mức độ phù hợp của mô hình với dữ liệu thực tế. Để làm được điều này, người phân tích thường sử dụng R bình phương (R²) và R bình phương hiệu chỉnh (Adjusted R²) – hai chỉ số cốt lõi giúp xác định mô hình hồi quy tuyến tính có phản ánh đúng dữ liệu hay không.
Mục lục
Toggle1. R² là gì?
R bình phương (R²), hay còn gọi là hệ số xác định, là chỉ số phản ánh tỷ lệ phần trăm biến thiên của biến phụ thuộc (Y) được giải thích bởi các biến độc lập (X) trong mô hình hồi quy tuyến tính.
Về bản chất, R² được tính từ ý tưởng rằng tổng biến thiên của Y có thể chia làm hai phần:
- Biến thiên do hồi quy (Regression Sum of Squares – SSR): phần biến thiên được mô hình giải thích.
- Biến thiên do phần dư (Residual Sum of Squares – SSE): phần biến thiên không được mô hình giải thích.
Công thức tổng quát: R2=1−SSESSTR^2 = 1 – \frac{SSE}{SST}R2=1−SSTSSE
trong đó:
- SSE: Tổng bình phương sai số,
- SST: Tổng bình phương độ lệch của Y so với trung bình.
Khi SSE càng nhỏ, nghĩa là các điểm dữ liệu càng gần đường hồi quy → mô hình càng phù hợp → R² càng cao.
Tuy nhiên, một nhược điểm lớn của R² là nó luôn tăng khi bạn thêm nhiều biến độc lập vào mô hình – kể cả khi những biến này không thật sự có ý nghĩa thống kê. Điều đó khiến R² có xu hướng “thổi phồng” độ phù hợp của mô hình.
2. R² hiệu chỉnh là gì? — Phiên bản trung thực hơn của R²

Để khắc phục nhược điểm trên, người ta sử dụng R bình phương hiệu chỉnh (Adjusted R²).
Chỉ số này điều chỉnh R² dựa trên số lượng biến độc lập và kích thước mẫu, phản ánh mức độ phù hợp thực sự của mô hình hồi quy.
Công thức: Rhiệu chỉnh2=1−(1−R2)(n−1)n−k−1R^2_{hiệu\ chỉnh} = 1 – \frac{(1 – R^2)(n – 1)}{n – k – 1}Rhiệu chỉnh2=1−n−k−1(1−R2)(n−1)
trong đó:
- n: số quan sát,
- k: số biến độc lập.
Khi thêm một biến mới vào mô hình:
- Nếu biến đó thực sự giúp cải thiện mô hình, Adjusted R² sẽ tăng.
- Nếu biến không có ý nghĩa, Adjusted R² sẽ giảm.
Do đó, R² hiệu chỉnh luôn nhỏ hơn hoặc bằng R², và được xem là thước đo đáng tin cậy hơn khi đánh giá mô hình hồi quy đa biến.
3. Ý nghĩa của R² hiệu chỉnh trong thực tế
Giống như R², chỉ số R² hiệu chỉnh dao động từ 0 đến 1:
- Giá trị càng gần 1 → mô hình càng giải thích tốt biến phụ thuộc.
- Giá trị càng gần 0 → mô hình giải thích kém.
Ví dụ:
Giả sử trong kết quả hồi quy SPSS, Adjusted R² = 0.725, điều đó có nghĩa:
Các biến độc lập trong mô hình giải thích được 72.5% sự biến thiên của biến phụ thuộc.
Phần còn lại 27.5% là do các yếu tố chưa được đưa vào mô hình và sai số ngẫu nhiên.
4. Khi R² hiệu chỉnh dưới 0.5 — Có phải mô hình kém?
Nhiều người cho rằng R² hiệu chỉnh phải trên 0.5 (50%) thì mô hình mới “đạt yêu cầu”, nhưng thực tế không có tiêu chuẩn cố định nào như vậy.
Mức độ phù hợp của mô hình phụ thuộc vào:
- Tính chất của hiện tượng nghiên cứu,
- Số lượng biến độc lập,
- Độ chính xác của dữ liệu,
- Ngành khoa học cụ thể.
Trong một số lĩnh vực xã hội, hành vi, hoặc marketing, Adjusted R² < 0.5 vẫn hoàn toàn chấp nhận được, miễn là các biến có ý nghĩa thống kê và mô hình phù hợp về mặt lý thuyết.
Nói cách khác, R² hiệu chỉnh chỉ là thước đo tham khảo, không nên dùng để bác bỏ mô hình một cách cứng nhắc.
5. Cách tăng giá trị R² & R² hiệu chỉnh trong SPSS
Nếu kết quả hồi quy của bạn cho thấy R² hiệu chỉnh thấp, có thể cải thiện bằng các cách sau:
5.1. Loại bỏ các giá trị ngoại lai (Outliers) qua đồ thị Scatter Plot

Các điểm dị biệt (outliers) thường làm sai lệch mô hình và kéo giảm giá trị R² hiệu chỉnh.
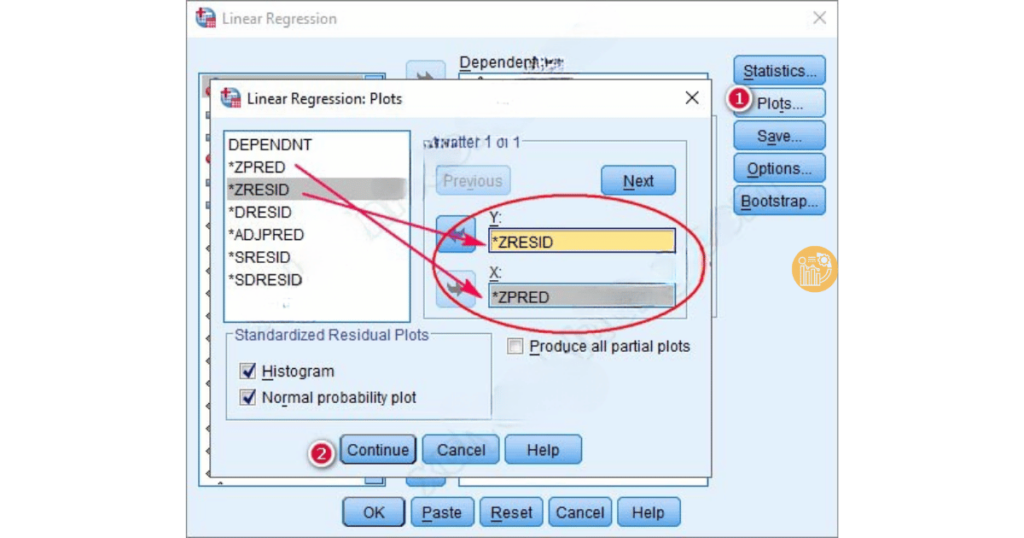
Trong SPSS, bạn có thể phát hiện chúng bằng cách:
- Vào Plots, kéo ZRESID vào ô Y và ZPRED vào ô X.
- Quan sát đồ thị Scatter Plot:
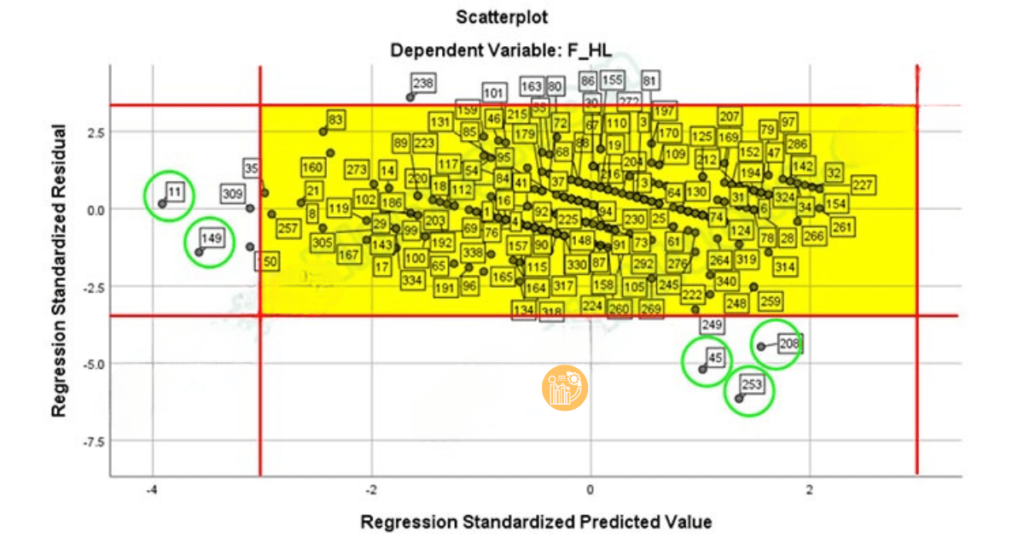
Các điểm nằm ngoài vùng −3,3-3, 3−3,3 theo quy luật Empirical 68–95–99.7 là các giá trị ngoại lai.
Ví dụ: mô hình hồi quy giữa F_TL, F_CV → F_HL ban đầu có Adjusted R² = 0.478.
Sau khi loại bỏ 5 điểm dị biệt (ID: 11, 45, 149, 208, 253), Adjusted R² tăng lên 0.553, chứng tỏ mô hình đã phù hợp hơn đáng kể.

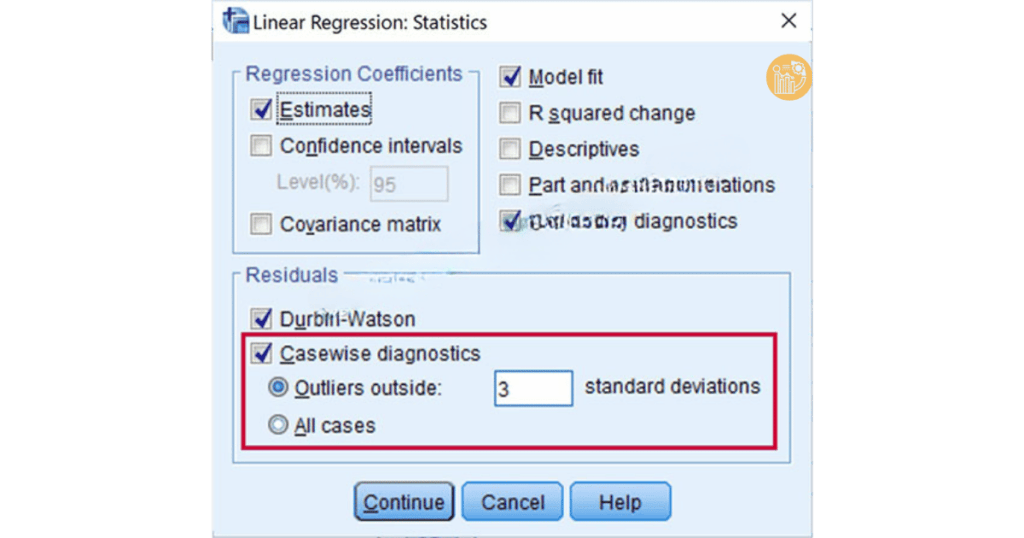
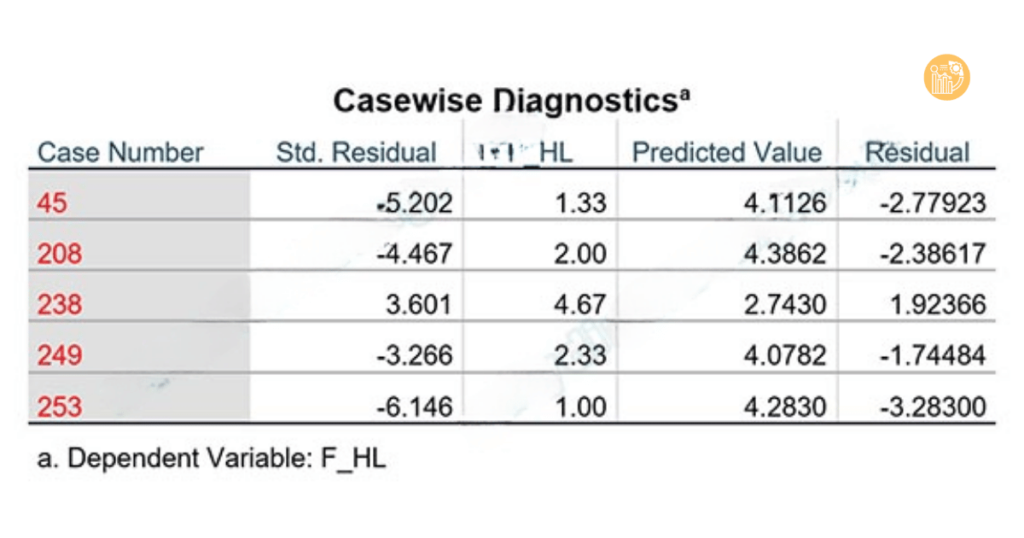
5.2. Sử dụng bảng Casewise Diagnostics trong SPSS
SPSS hỗ trợ phát hiện tự động điểm dị biệt:
- Chọn Statistics → Casewise Diagnostics,
- Nhập giá trị 3 trong ô Outliers outside, để xác định các quan sát nằm ngoài vùng ±3 độ lệch chuẩn.
Sau khi loại bỏ các điểm này, Adjusted R² có thể tăng đáng kể.
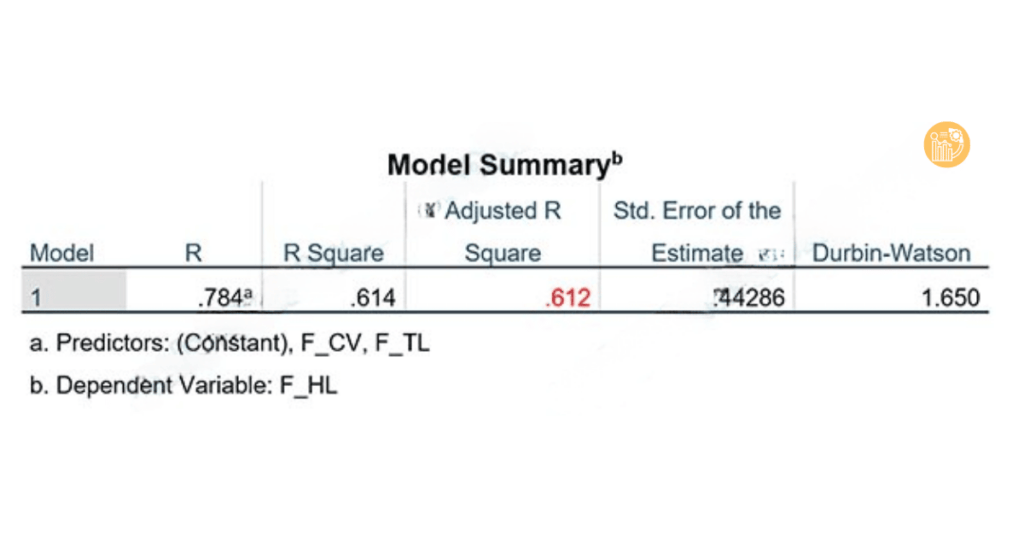
Ví dụ: loại bỏ các quan sát 45, 208, 238, 249, 253 giúp mô hình tăng Adjusted R² từ 0.478 lên 0.612, thể hiện sự cải thiện rõ rệt về độ phù hợp.
6. Kết luận
R bình phương hiệu chỉnh là chỉ số then chốt giúp đánh giá mức độ phù hợp thực chất của mô hình hồi quy tuyến tính.
Khác với R² thông thường, chỉ số hiệu chỉnh phản ánh độ chính xác sau khi đã loại trừ ảnh hưởng “ảo” của việc thêm biến độc lập.
Một mô hình tốt không nhất thiết phải có Adjusted R² cao vượt trội, mà cần:
- Các biến có ý nghĩa thống kê,
- Phù hợp về lý thuyết,
- Không vi phạm giả định hồi quy,
- Không bị ảnh hưởng bởi các giá trị ngoại lai.
Do đó, khi phân tích hồi quy trong SPSS, hãy ưu tiên xem xét R² hiệu chỉnh thay vì R² thuần túy, và chủ động kiểm tra – loại bỏ outlier để đảm bảo mô hình phản ánh đúng thực tế.