Trong thống kê, khi làm việc với các tập số liệu, một trong những câu hỏi quan trọng nhất là: “Giá trị trung tâm của dữ liệu nằm ở đâu?”. Để trả lời câu hỏi này, thống kê mô tả sử dụng nhiều thước đo khác nhau, trong đó trung vị (median) đóng vai trò rất quan trọng. Hiểu rõ cách tính trung vị trong thống kê giúp người học và người làm phân tích dữ liệu đánh giá tập dữ liệu chính xác hơn, đặc biệt khi dữ liệu có giá trị ngoại lai.
Bài viết này do xulysolieu.info (Xử lý số liệu) biên soạn, nhằm giải thích một cách dễ hiểu Trung vị (Median) là gì? Cách tính và ví dụ minh họa, bản chất của median, cách tính trung vị trong thống kê và các ví dụ minh họa cụ thể để bạn có thể áp dụng ngay trong thực tế.
Mục lục
ToggleTrung vị (Median) là gì?
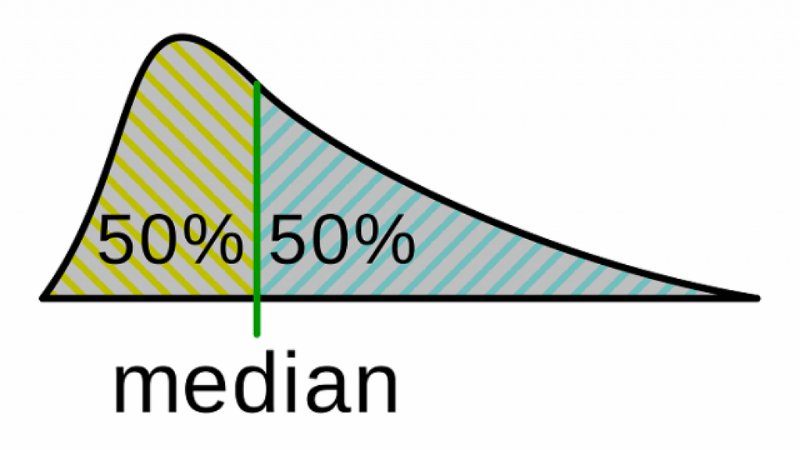
Trung vị, trong tiếng Anh gọi là median, là giá trị nằm ở chính giữa của một tập dữ liệu sau khi các giá trị đã được sắp xếp theo thứ tự tăng dần hoặc giảm dần. Nói cách khác, trung vị chia tập dữ liệu thành hai nửa bằng nhau: một nửa các giá trị nhỏ hơn hoặc bằng trung vị và một nửa các giá trị lớn hơn hoặc bằng trung vị.
Trong thống kê mô tả, trung vị là một trong những thước đo quan trọng để đo lường xu hướng trung tâm của dữ liệu, bên cạnh giá trị trung bình (mean) và mốt (mode). Tuy nhiên, trung vị có ưu điểm lớn là ít bị ảnh hưởng bởi các giá trị ngoại lai, do đó cách tính trung vị trong thống kê thường được ưu tiên trong nhiều tình huống phân tích dữ liệu thực tế.
Vai trò của trung vị trong thống kê mô tả
Trong quá trình phân tích dữ liệu, đặc biệt là với dữ liệu định lượng, việc lựa chọn thước đo xu hướng trung tâm phù hợp là rất quan trọng. Trung vị thường được sử dụng khi:
- Dữ liệu có phân phối lệch (lệch trái hoặc lệch phải).
- Tồn tại các giá trị ngoại lai làm sai lệch giá trị trung bình.
- Cần mô tả “vị trí điển hình” của dữ liệu thay vì giá trị trung bình toán học.
Nhờ đó, cách tính trung vị trong thống kê giúp phản ánh chính xác hơn bản chất của dữ liệu so với việc chỉ dựa vào trung bình cộng.
Cách tính trung vị trong thống kê

Để áp dụng đúng cách tính trung vị trong thống kê, bạn cần thực hiện theo các bước cơ bản sau:
- Sắp xếp toàn bộ tập dữ liệu theo thứ tự tăng dần hoặc giảm dần.
- Xác định số lượng quan sát trong tập dữ liệu.
- Tùy thuộc vào số lượng quan sát là lẻ hay chẵn, áp dụng quy tắc tính trung vị phù hợp.
Dưới đây là hướng dẫn chi tiết cho từng trường hợp.
Cách tính trung vị trong thống kê với số quan sát lẻ
Khi tập dữ liệu có số lượng quan sát là số lẻ, cách tính trung vị trong thống kê khá đơn giản. Trung vị chính là giá trị nằm ở vị trí giữa của dãy số đã được sắp xếp.
Ví dụ:
Xét tập dữ liệu: {3, 13, 2, 34, 11, 26, 47}
Bước 1: Sắp xếp dữ liệu theo thứ tự tăng dần:
{2, 3, 11, 13, 26, 34, 47}
Bước 2: Xác định vị trí ở giữa. Với 7 giá trị, vị trí trung tâm là giá trị thứ 4.
Như vậy, trung vị của tập dữ liệu này là 13.
Trong trường hợp này, median cho thấy giá trị trung tâm hợp lý của dữ liệu, ngay cả khi có những giá trị lớn như 34 hay 47.
Cách tính trung vị trong thống kê với số quan sát chẵn
Khi tập dữ liệu có số lượng quan sát là số chẵn, sẽ không tồn tại một giá trị duy nhất nằm chính giữa. Lúc này, cách tính trung vị trong thống kê là lấy trung bình cộng của hai giá trị nằm ở giữa.
Ví dụ:
Xét tập dữ liệu: {3, 13, 2, 34, 11, 17, 27, 47}
Bước 1: Sắp xếp dữ liệu theo thứ tự tăng dần:
{2, 3, 11, 13, 17, 27, 34, 47}
Bước 2: Xác định hai giá trị ở giữa, đó là giá trị thứ 4 và thứ 5 (13 và 17).
Bước 3: Tính trung bình của hai giá trị này:
(13 + 17) / 2 = 15
Vậy trung vị của tập dữ liệu là 15.
So sánh trung vị và giá trị trung bình
Trong đo lường xu hướng trung tâm, nhiều người thường nhầm lẫn giữa trung vị và trung bình. Tuy nhiên, hai khái niệm này có ý nghĩa khác nhau trong phân tích dữ liệu.
- Giá trị trung bình phản ánh giá trị “bình quân” của dữ liệu, nhưng rất nhạy cảm với ngoại lai.
- Trung vị phản ánh vị trí trung tâm của dữ liệu và ít bị ảnh hưởng bởi các giá trị cực đoan.
Ví dụ, trong phân tích thu nhập, một vài cá nhân có thu nhập rất cao có thể kéo giá trị trung bình lên, trong khi trung vị vẫn phản ánh mức thu nhập điển hình của đa số. Do đó, cách tính trung vị trong thống kê thường được ưu tiên trong các báo cáo kinh tế – xã hội.
Ứng dụng của trung vị trong phân tích dữ liệu
Trong thực tế, trung vị được ứng dụng rộng rãi trong nhiều lĩnh vực:
- Phân tích thu nhập, tiền lương và mức sống.
- Đánh giá kết quả học tập và điểm số.
- Phân tích dữ liệu y tế như thời gian nằm viện, chi phí điều trị.
- Thống kê mô tả trong nghiên cứu khoa học và khảo sát xã hội.
Việc nắm vững cách tính trung vị trong thống kê giúp người làm phân tích dữ liệu lựa chọn chỉ tiêu phù hợp, tránh diễn giải sai lệch khi dữ liệu không phân phối chuẩn.
Những lưu ý khi sử dụng trung vị
Khi áp dụng cách tính trung vị trong thống kê, bạn cần lưu ý một số điểm sau:
- Trung vị chỉ áp dụng cho dữ liệu định lượng hoặc dữ liệu thứ bậc.
- Luôn sắp xếp dữ liệu trước khi xác định trung vị.
- Không nhầm lẫn trung vị với trung bình cộng.
- Trong báo cáo, nên kết hợp trung vị với các chỉ tiêu khác để mô tả đầy đủ dữ liệu.
Kết luận
Trung vị là một thước đo quan trọng trong thống kê mô tả, giúp đo lường xu hướng trung tâm của dữ liệu một cách ổn định và đáng tin cậy. Hiểu rõ bản chất median và thành thạo cách tính trung vị trong thống kê sẽ giúp bạn phân tích dữ liệu định lượng chính xác hơn, đặc biệt trong những trường hợp dữ liệu có ngoại lai hoặc phân phối lệch.
Nếu bạn cần hỗ trợ học thống kê, phân tích dữ liệu, hoặc áp dụng cách tính trung vị trong thống kê vào bài tập, luận văn và nghiên cứu khoa học, hãy tham khảo tại xulysolieu.info (Xử lý số liệu) hoặc liên hệ 0878968468 để được tư vấn chi tiết.