Trong phân tích dữ liệu, một yêu cầu bắt buộc khi xây dựng mô hình hồi quy tuyến tính là phải đánh giá mức độ phù hợp của mô hình với dữ liệu thực tế. Để làm được điều này, nhà nghiên cứu thường sử dụng các chỉ số đo lường mức độ giải thích của mô hình. Trong số đó, tính R là nội dung được quan tâm nhiều nhất, đặc biệt khi làm việc với SPSS và các nghiên cứu định lượng.

Bài viết này tập trung giải thích bản chất của việc tính R, sự khác nhau giữa R bình phương và R bình phương hiệu chỉnh, cách diễn giải kết quả, cũng như các kỹ thuật thường dùng để cải thiện chỉ số này trong hồi quy tuyến tính. Nội dung được trình bày theo hướng giáo dục, dễ hiểu và sát với thực hành phân tích dữ liệu.

1. Tính R và vai trò trong hồi quy tuyến tính

Tính R trong hồi quy tuyến tính thường được hiểu thông qua hệ số xác định R bình phương, hay còn gọi là r squared. Đây là chỉ số phản ánh mức độ mà các biến độc lập giải thích được sự biến thiên của biến phụ thuộc trong mô hình.

Khi thực hiện hồi quy tuyến tính, dữ liệu quan sát của biến phụ thuộc luôn có sự biến thiên. Phần biến thiên này có thể được chia thành hai phần: phần được giải thích bởi mô hình hồi quy và phần còn lại do sai số ngẫu nhiên. Việc tính R giúp đo lường tỷ lệ phần biến thiên được mô hình giải thích so với tổng biến thiên quan sát được.

2. R bình phương là gì?

R bình phương là một chỉ số phổ biến trong đánh giá mô hình hồi quy. Giá trị của R bình phương nằm trong khoảng từ 0 đến 1. Khi giá trị này càng tiến về 1, mô hình hồi quy càng giải thích tốt sự biến thiên của biến phụ thuộc.

Ví dụ, nếu kết quả hồi quy cho thấy R bình phương bằng 0.7, điều đó có nghĩa là khoảng 70% sự biến thiên của biến phụ thuộc được giải thích bởi các biến độc lập trong mô hình. Phần còn lại 30% đến từ các yếu tố khác ngoài mô hình và sai số.

Tuy nhiên, một điểm quan trọng cần lưu ý khi tính R là R bình phương luôn có xu hướng tăng khi thêm biến độc lập vào mô hình, ngay cả khi biến đó không thực sự có ý nghĩa.

3. Hạn chế của R bình phương

Mặc dù được sử dụng rộng rãi, R bình phương tồn tại một hạn chế lớn. Cụ thể, chỉ số này không giảm khi thêm biến độc lập vào mô hình. Điều này có thể dẫn đến việc đánh giá quá cao mức độ phù hợp của mô hình, đặc biệt trong hồi quy tuyến tính đa biến.

Do đó, chỉ dựa vào R bình phương để đánh giá mô hình là chưa đủ an toàn trong phân tích dữ liệu. Đây chính là lý do R bình phương hiệu chỉnh ra đời.

4. R bình phương hiệu chỉnh là gì?

R bình phương hiệu chỉnh được phát triển dựa trên R bình phương nhằm khắc phục hạn chế kể trên. Khi tính R bình phương hiệu chỉnh, chỉ số này đã điều chỉnh theo số lượng biến độc lập và cỡ mẫu.

Khác với R bình phương, R bình phương hiệu chỉnh có thể tăng hoặc giảm khi thêm biến độc lập vào mô hình. Nếu biến mới không thực sự cải thiện khả năng giải thích, giá trị này sẽ giảm. Vì vậy, R bình phương hiệu chỉnh phản ánh sát hơn chất lượng thực sự của mô hình hồi quy tuyến tính.

Trong thực hành phân tích dữ liệu, việc tính R thường gắn liền với việc đọc và diễn giải R bình phương hiệu chỉnh thay vì chỉ nhìn vào R bình phương thông thường.

5. Ý nghĩa của R bình phương hiệu chỉnh

Giá trị R bình phương hiệu chỉnh cũng nằm trong khoảng từ 0 đến 1. Giá trị càng cao cho thấy mô hình có khả năng giải thích tốt hơn. Tuy nhiên, việc đạt giá trị gần bằng 1 là rất hiếm trong các nghiên cứu xã hội, kinh tế và hành vi.

Ví dụ, nếu R bình phương hiệu chỉnh bằng 0.72, điều đó có nghĩa là các biến độc lập trong mô hình giải thích được 72% sự biến thiên của biến phụ thuộc. Phần còn lại đến từ các yếu tố chưa được đưa vào mô hình và sai số ngẫu nhiên.

6. R bình phương hiệu chỉnh dưới 0.5 có chấp nhận được không

Một câu hỏi rất phổ biến khi tính R là liệu R bình phương hiệu chỉnh dưới 0.5 có làm mô hình bị loại hay không. Trên thực tế, không tồn tại một ngưỡng cứng nào cho R bình phương hiệu chỉnh.

Giá trị này phụ thuộc vào bản chất nghiên cứu, số lượng biến độc lập và lĩnh vực nghiên cứu. Trong các mô hình đơn giản hoặc nghiên cứu hành vi con người, R bình phương hiệu chỉnh dưới 0.5 vẫn hoàn toàn có thể chấp nhận được.

Việc yêu cầu R bình phương hiệu chỉnh luôn lớn hơn 0.5 trong mọi trường hợp là không phù hợp với lý thuyết thống kê và thực tiễn nghiên cứu.

7. Cách cải thiện giá trị khi tính R

Trong phân tích dữ liệu, có một số kỹ thuật giúp cải thiện kết quả tính R, đặc biệt là R bình phương hiệu chỉnh. Một trong những cách phổ biến nhất là kiểm tra và xử lý các giá trị ngoại lai.

Các điểm dữ liệu dị biệt có thể làm méo mó đường hồi quy và kéo giảm mức độ phù hợp của mô hình. Do đó, việc phát hiện và xử lý outliers là bước quan trọng trước khi kết luận về chất lượng mô hình.

8. Cải thiện R bình phương thông qua đồ thị Scatter Plot hồi quy

Xét một ví dụ hồi quy tuyến tính bội trong đó hai biến độc lập F_TL và F_CV được sử dụng để giải thích biến phụ thuộc F_HL. Trong bảng Model Summary, hệ số Adjusted R Square ban đầu đạt giá trị 0.478. Chỉ số này phản ánh mức độ phù hợp của mô hình hồi quy; giá trị càng tiến gần 1 cho thấy mô hình càng giải thích tốt sự biến thiên của biến phụ thuộc.

Cách tăng R bình phương trong SPSS

Để xây dựng đồ thị Scatter Plot khi chạy hồi quy tuyến tính bội trong SPSS, người phân tích truy cập vào mục Plots, sau đó:

• Đưa biến ZRESID vào trục Y
• Đưa biến ZPRED vào trục X

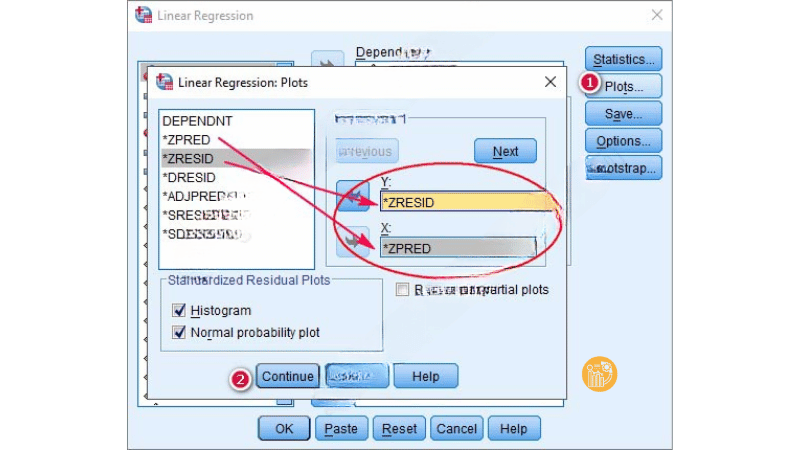
Thiết lập này cho phép quan sát mối quan hệ giữa phần dư chuẩn hóa và giá trị dự báo chuẩn hóa, từ đó phát hiện các quan sát bất thường.

Cách cải thiện Adjusted R Square trong SPSS

Việc thực hiện hồi quy cần tuân thủ đầy đủ quy trình phân tích để SPSS xuất ra toàn bộ bảng kết quả và đồ thị cần thiết, trong đó có Scatter Plot phục vụ đánh giá mô hình.

Theo quy luật Empirical (68–95–99.7) của phân phối chuẩn, các quan sát nằm ngoài khoảng từ –3 đến +3 độ lệch chuẩn trên cả hai trục thường được xem là điểm dị biệt. Trong đồ thị, có thể nhận thấy 5 quan sát (được đánh dấu khác biệt) nằm ngoài vùng phân bố chính.

Để xác định chính xác mã số các quan sát này, người dùng nhấp đúp vào đồ thị Scatter, kích hoạt chế độ hiển thị nhãn quan sát và đóng cửa sổ chỉnh sửa sau khi hoàn tất. Kết quả cho thấy các điểm dị biệt tương ứng với các quan sát: 11, 45, 149, 208 và 253.

Tiếp theo, tiến hành loại bỏ 5 quan sát trên khỏi tập dữ liệu. Để tránh nhầm lẫn, nên tạo một biến đánh số thứ tự cho các dòng dữ liệu và xóa theo thứ tự từ dòng có số lớn đến số nhỏ. Sau đó, chạy lại hồi quy tuyến tính bội với tập dữ liệu đã được làm sạch.

Kết quả cho thấy Adjusted R Square tăng lên 0.553, cao hơn đáng kể so với mức ban đầu 0.478. Mặc dù phải loại bỏ 5 quan sát, nhưng so với tổng cỡ mẫu 350, tỷ lệ này là rất nhỏ và hoàn toàn chấp nhận được để đổi lấy một mô hình hồi quy phù hợp hơn.

9. Cải thiện R bình phương bằng bảng Casewise Diagnostics

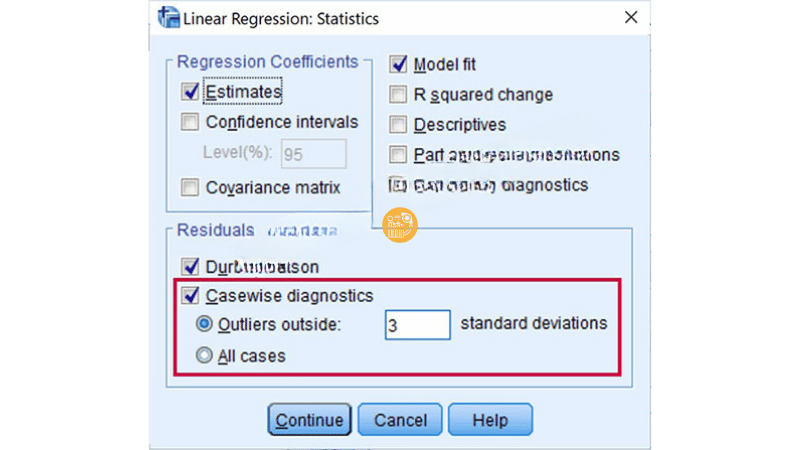
Ngoài Scatter Plot, SPSS còn cung cấp công cụ Casewise Diagnostics để tự động phát hiện các quan sát dị biệt trong phân tích hồi quy tuyến tính. Tại mục Statistics, người dùng tích chọn Casewise diagnostics và nhập ngưỡng 2 hoặc 3 độ lệch chuẩn vào ô Outliers outside.

Thông thường, nên bắt đầu với ngưỡng 3 độ lệch chuẩn. Nếu sau khi xử lý các điểm này mà mô hình vẫn chưa đạt yêu cầu, có thể xem xét tiếp các điểm nằm ngoài 2 độ lệch chuẩn.

Cách tăng R² trong SPSS bằng Casewise Diagnostics

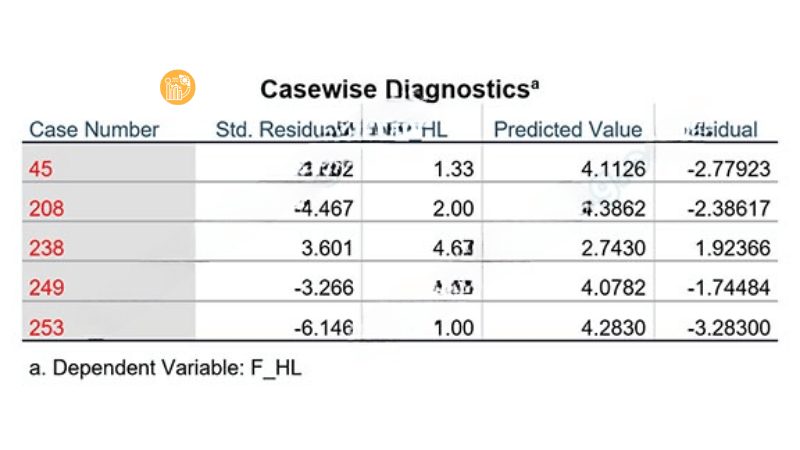
Tiếp tục phân tích hồi quy với hai biến độc lập F_TL và F_CV tác động lên F_HL, thiết lập Casewise Diagnostics với ngưỡng 3 độ lệch chuẩn. Kết quả ban đầu cho thấy Adjusted R Square vẫn ở mức 0.478, đồng thời bảng Casewise Diagnostics xác định các quan sát dị biệt gồm: 45, 208, 238, 249 và 253.

Tiến hành loại bỏ 5 quan sát này khỏi dữ liệu (lưu ý thao tác xóa từ dòng có số thứ tự lớn xuống nhỏ), sau đó chạy lại mô hình hồi quy.

Kết quả cuối cùng cho thấy Adjusted R Square tăng lên 0.612, cao hơn đáng kể so với giá trị ban đầu. Điều này cho thấy việc loại bỏ các quan sát dị biệt đã giúp mô hình hồi quy cải thiện rõ rệt về mức độ phù hợp.

10. Lưu ý khi cải thiện R bình phương

Mặc dù việc loại bỏ outliers giúp tăng giá trị khi tính R, nhưng cần thực hiện một cách thận trọng. Việc loại bỏ dữ liệu phải có cơ sở thống kê và logic thực tế, tránh việc loại bỏ tùy tiện chỉ để làm đẹp kết quả.

Mục tiêu của phân tích dữ liệu không phải là tối đa hóa R bình phương bằng mọi giá, mà là xây dựng một mô hình có ý nghĩa và phản ánh đúng bản chất hiện tượng nghiên cứu.

Ứng dụng thực tế trong phân tích dữ liệu

Tại xulysolieu.info và Xử lý số liệu, nội dung về tính R, đánh giá mô hình hồi quy và đọc kết quả SPSS luôn được hướng dẫn chi tiết trong các khóa học phân tích dữ liệu. Người học không chỉ biết cách chạy hồi quy mà còn hiểu rõ ý nghĩa từng chỉ số.

Kết luận

Tóm lại, tính R là bước quan trọng để đánh giá mức độ phù hợp của mô hình hồi quy tuyến tính. Trong thực hành, R bình phương hiệu chỉnh là chỉ số nên được ưu tiên sử dụng vì phản ánh sát hơn chất lượng mô hình.