Cách đánh giá chỉ số Model Fit trong CFA: Hướng dẫn chi tiết và ví dụ thực tế
Giới thiệu
Sau khi thực hiện phân tích nhân tố khám phá (EFA), bước tiếp theo trong việc xây dựng mô hình là kiểm tra độ phù hợp mô hình (Model Fit) trong phân tích nhân tố khẳng định (CFA). Việc đánh giá độ phù hợp của mô hình là một trong những bước quan trọng nhất trong quá trình phân tích dữ liệu, giúp bạn xác nhận liệu mô hình đo lường của mình có phản ánh chính xác các khái niệm nghiên cứu hay không. Các chỉ số độ phù hợp mô hình cung cấp những thông tin quan trọng về mức độ khớp giữa dữ liệu thực tế và mô hình lý thuyết.
Trong bài viết này, chúng tôi sẽ hướng dẫn chi tiết cách đánh giá chỉ số Model Fit trong CFA, giải thích các chỉ số phổ biến như CFI, TLI, RMSEA và cung cấp ví dụ thực tế để bạn dễ dàng áp dụng vào nghiên cứu của mình.
Model Fit là gì?
Model Fit trong CFA là quá trình kiểm tra xem mô hình cấu trúc của bạn có khớp với dữ liệu quan sát hay không. Mô hình đo lường trong CFA thường bao gồm các thang đo (scales) và các biến tiềm ẩn (latent variables), giúp đo lường các khái niệm trong nghiên cứu. Để đảm bảo mô hình của bạn là chính xác và có tính ứng dụng cao, cần phải kiểm tra các chỉ số độ phù hợp mô hình như CFI, TLI, RMSEA, và các chỉ số khác.
Các chỉ số độ phù hợp mô hình (Model Fit) trong CFA
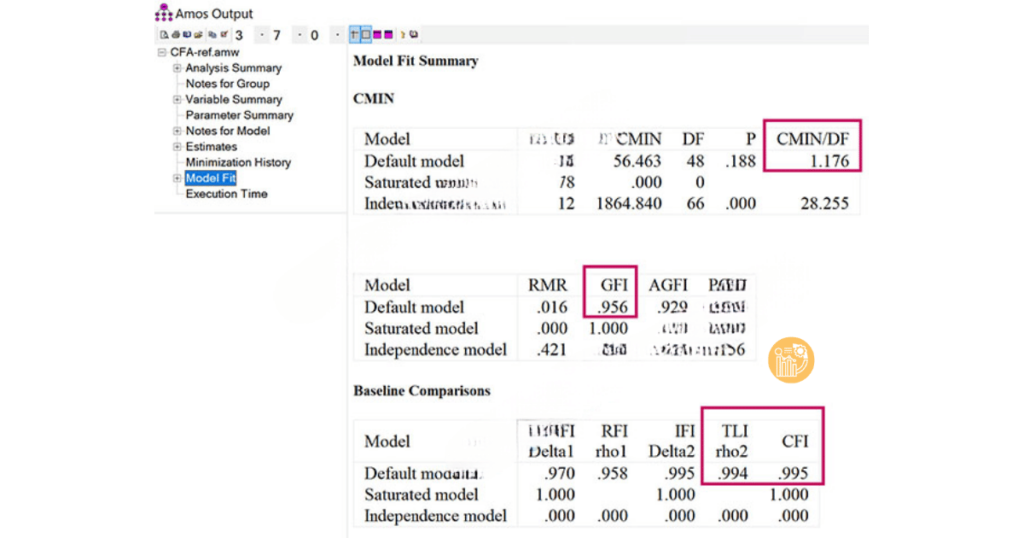
- CMIN/df (Chi-square / degrees of freedom): CMIN/df là tỷ lệ giữa giá trị Chi-square và bậc tự do của mô hình. Chỉ số này giúp đánh giá mức độ phù hợp của mô hình với dữ liệu. Theo tiêu chuẩn của Hu & Bentler (1999), CMIN/df ≤ 3 là tốt, còn CMIN/df ≤ 5 có thể chấp nhận được.
- CFI (Comparative Fit Index): CFI là một trong các chỉ số độ phù hợp phổ biến trong CFA, đánh giá mức độ phù hợp của mô hình với dữ liệu quan sát. Chỉ số này có giá trị từ 0 đến 1, với giá trị càng cao cho thấy mô hình càng phù hợp. Theo tiêu chuẩn, CFI ≥ 0.9 là tốt, CFI ≥ 0.95 là rất tốt, và CFI ≥ 0.8 có thể chấp nhận được.
- TLI (Tucker-Lewis Index): TLI, hay còn gọi là Non-Normed Fit Index (NNFI), đo lường mức độ cải thiện mô hình so với mô hình cơ sở. TLI có giá trị từ 0 đến 1, và giá trị TLI ≥ 0.9 thường được coi là đạt yêu cầu, cho thấy mô hình có độ phù hợp tốt với dữ liệu.
- RMSEA (Root Mean Square Error of Approximation): RMSEA là chỉ số đánh giá sai số của mô hình, tính theo căn bậc hai của sai số bình phương. RMSEA có giá trị từ 0 đến 1, với giá trị thấp hơn 0.06 là tốt, và từ 0.06 đến 0.08 là có thể chấp nhận được.
- PCLOSE: PCLOSE kiểm tra giả thuyết về việc mô hình có khớp hoàn hảo với dữ liệu hay không. Giá trị PCLOSE ≥ 0.05 cho thấy mô hình phù hợp tốt với dữ liệu.
Tiêu chuẩn Model Fit trong CFA
Dưới đây là một số ngưỡng chuẩn phổ biến để đánh giá Model Fit theo các tác giả nghiên cứu:
- Theo Hu & Bentler (1999):
- CMIN/df ≤ 3 là tốt, CMIN/df ≤ 5 là chấp nhận được
- CFI ≥ 0.9 là tốt, CFI ≥ 0.95 là rất tốt, CFI ≥ 0.8 là chấp nhận được
- TLI ≥ 0.9 là tốt
- GFI ≥ 0.9 là tốt, GFI ≥ 0.95 là rất tốt
- RMSEA ≤ 0.06 là tốt, RMSEA ≤ 0.08 là chấp nhận được
- PCLOSE ≥ 0.05 là tốt, PCLOSE ≥ 0.01 là chấp nhận được
- Theo Hair et al. (2010):
- CMIN/df ≤ 2 là tốt, CMIN/df ≤ 5 là chấp nhận được
- CFI ≥ 0.9 là tốt, CFI ≥ 0.95 là rất tốt, CFI ≥ 0.8 là chấp nhận được
- GFI ≥ 0.9 là tốt, GFI ≥ 0.95 là rất tốt
- RMSEA ≤ 0.08 là tốt, RMSEA ≤ 0.03 là rất tốt
Trường hợp riêng của GFI
Chỉ số GFI (Goodness-of-Fit Index) có thể gặp vấn đề trong các nghiên cứu có cỡ mẫu nhỏ, khiến nó khó đạt được mức 0.9. Nếu GFI dưới 0.9, bạn có thể chấp nhận ngưỡng 0.8 theo nghiên cứu của Baumgartner và Homburg (1995), nếu đây là yêu cầu của bài nghiên cứu.
Cải thiện độ phù hợp mô hình trong CFA
Khi chỉ số Model Fit không đạt yêu cầu, một trong những cách để cải thiện là sử dụng Covariance Modification trong AMOS. Điều này giúp giảm giá trị Chi-square và cải thiện các chỉ số Model Fit bằng cách nối các sai số có chỉ số MI (Modification Indices) cao. Tuy nhiên, cần phải thận trọng và không lạm dụng quá nhiều việc nối các sai số, vì điều này có thể làm sai lệch kết quả và làm giảm độ chính xác của dữ liệu.
Đánh giá chất lượng biến quan sát trong CFA
Sau khi kiểm tra độ phù hợp tổng thể của mô hình, bạn cần đánh giá chất lượng của các biến quan sát trong CFA. Để làm điều này, bạn cần xem xét hai bảng kết quả quan trọng là Regression Weights và Standardized Regression Weights.
Regression Weights
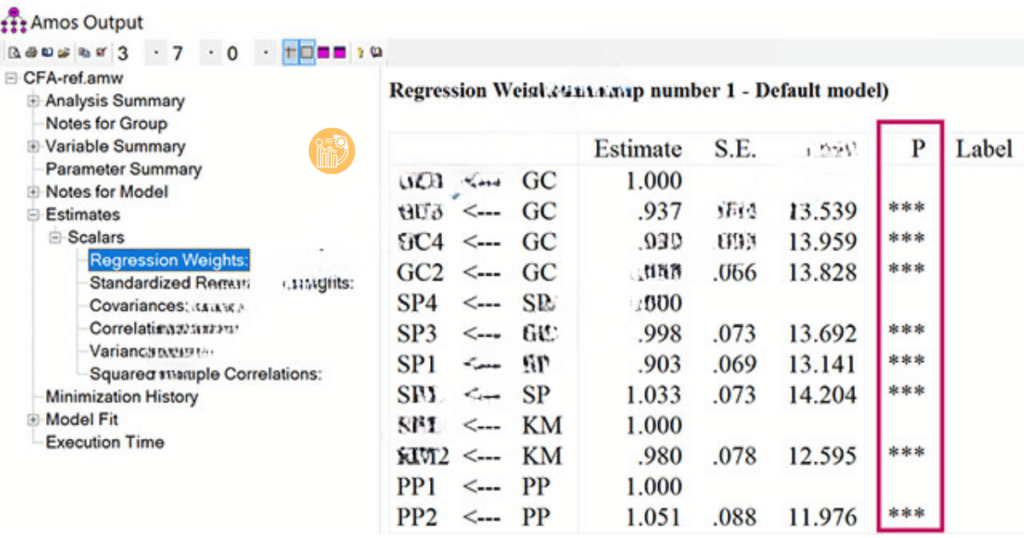
Bạn cần kiểm tra giá trị P (p-value) trong bảng Regression Weights để xác định xem biến quan sát có ý nghĩa trong mô hình hay không. Nếu p-value < 0.05, biến quan sát có ý nghĩa và có thể giữ lại trong mô hình. Nếu p-value > 0.05, biến quan sát không có ý nghĩa và cần loại bỏ.
Standardized Regression Weights
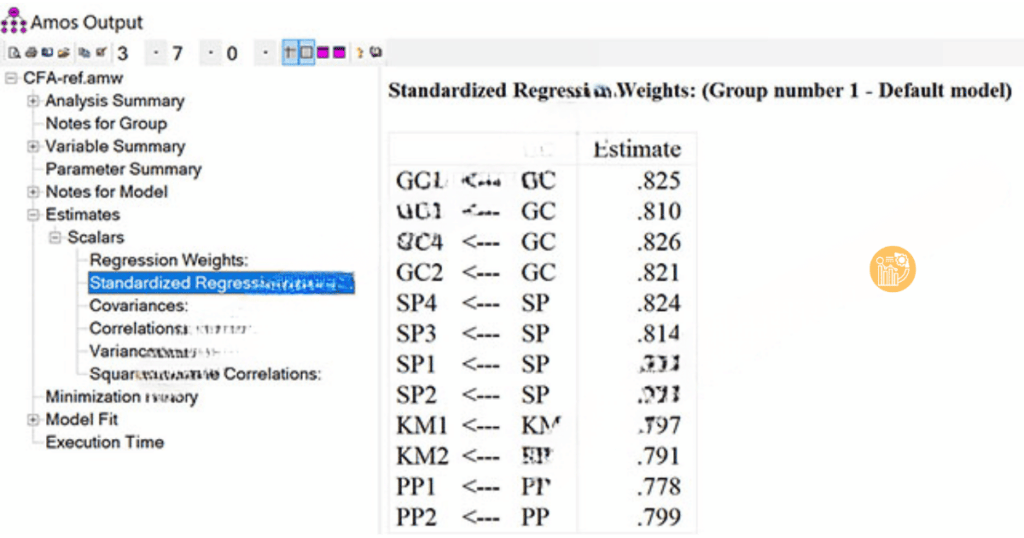
Theo Hair et al. (2010), những biến quan sát có Standardized Regression Weight từ 0.5 trở lên sẽ được giữ lại. Những biến có giá trị dưới 0.5 sẽ bị loại bỏ. Nếu biến có giá trị cao, điều này có nghĩa là biến quan sát đó đóng góp mạnh mẽ vào biến tiềm ẩn trong mô hình.
Cách đọc kết quả Model Fit trong SPSS và AMOS
Khi chạy CFA trong SPSS và AMOS, bạn sẽ nhận được các bảng kết quả bao gồm các chỉ số độ phù hợp mô hình như CMIN/df, CFI, RMSEA, TLI, và PCLOSE. Bạn cần kiểm tra từng chỉ số này để đảm bảo mô hình của bạn phù hợp với dữ liệu. Ngoài ra, bạn cũng cần kiểm tra các biến quan sát trong bảng Regression Weights và Standardized Regression Weights để đánh giá xem các biến có đóng góp vào mô hình hay không.
Kết luận
Kiểm định độ phù hợp mô hình (Model Fit) trong CFA là một bước quan trọng để đánh giá xem mô hình đo lường của bạn có phản ánh chính xác các khái niệm nghiên cứu hay không. Các chỉ số như CFI, TLI, RMSEA và PCLOSE giúp bạn kiểm tra mức độ phù hợp của mô hình với dữ liệu quan sát. Để cải thiện độ phù hợp mô hình, bạn có thể sử dụng các phương pháp điều chỉnh như Covariance Modification trong AMOS. Nếu bạn gặp khó khăn khi phân tích CFA trong SPSS và AMOS, hãy tham khảo dịch vụ hỗ trợ từ xulysolieu.info để tối ưu hóa kết quả và tiết kiệm thời gian.
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy AMOS – AMOS 09
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
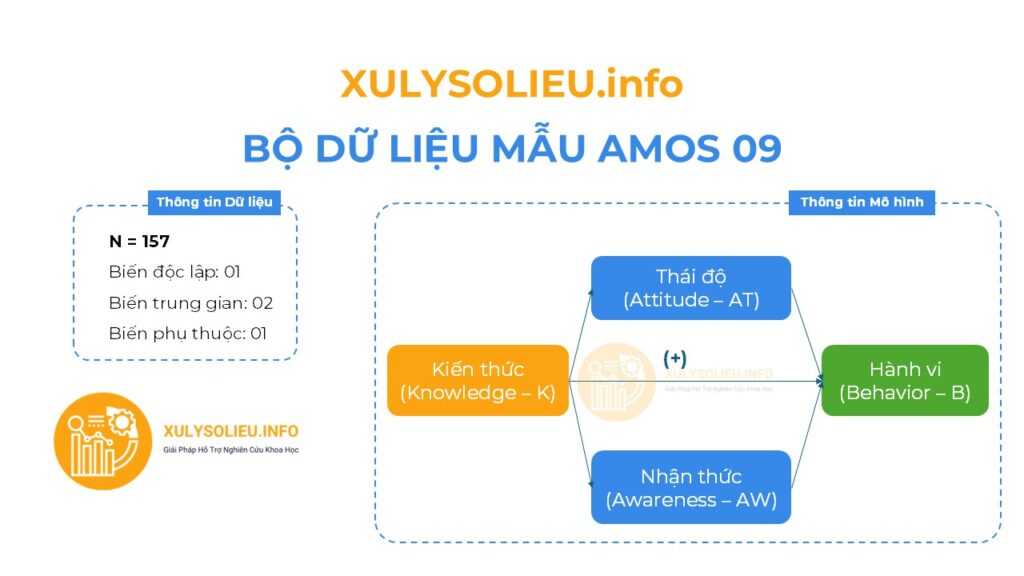
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 157
- Mô hình nghiên cứu bao gồm 04 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (thang đo Likert 5)
- Biến độc lập: 01
+ Thang đo Kiến thức (Knowledge – K) – 4 items - Biến trung gian: 02
+ Thang đo Thái độ (Attitude – AT) – 4 items
+ Thang đo Nhận thức (Awareness – AW) – 4 items - Biến phụ thuộc: 01
+ Thang đo Hành vi (Behavior – B) – 4 items
2. Chi tiết kết quả kiểm định
- Output File từ gói Dữ Liệu Mẫu:
+ File dữ liệu excel
+ File văn bản kết quả
+ File kết quả xử lý từ phần mềm - Link xem trước kết quả dữ liệu mẫu: Tại đây!
Giá gốc: 499k VND- Giá ưu đãi: 268k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI
Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy AMOS – AMOS 10
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
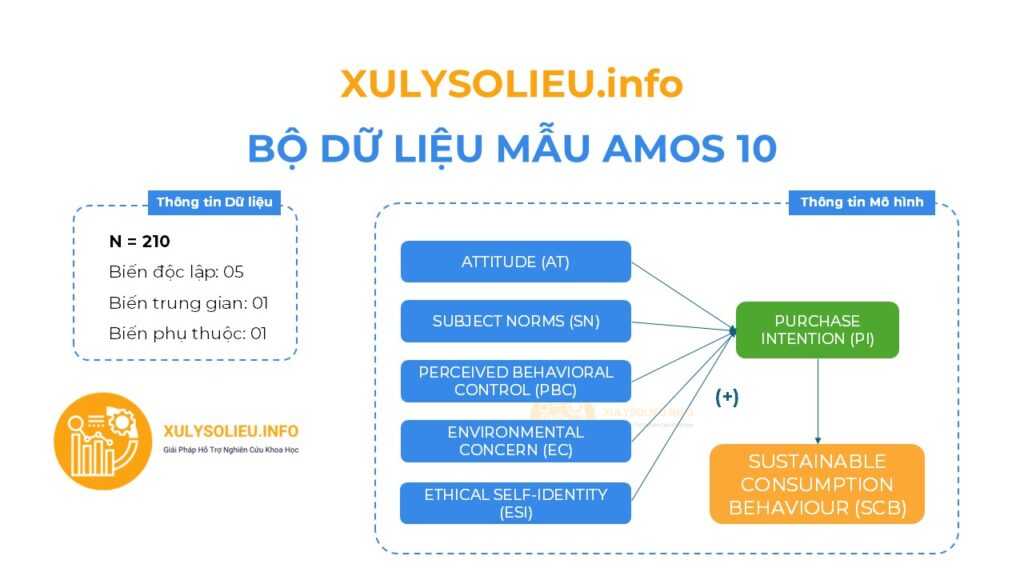
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 210
- Mô hình nghiên cứu bao gồm 07 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (thang đo Likert 5)
- Biến độc lập:
+ Attitude (AT): 3 items
+ Subject Norms (SN): 3 items
+ Perceived Behavioral Control (PBC): 3 items
+ Environmental Concern (EC): 3 items
+ Ethical Self-Identity (ESI): 3 items - Biến trung gian: Purchase Intention (PI): 3 items
- Biến phụ thuộc: Sustainable Consumption Behaviour (SCB): 3 items
2. Chi tiết kết quả kiểm định
- Output File từ gói Dữ Liệu Mẫu:
+ File dữ liệu excel
+ File văn bản kết quả
+ File kết quả xử lý từ phần mềm - Link xem trước kết quả dữ liệu mẫu: Tại đây!
Giá gốc: 499k VND- Giá ưu đãi: 268k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI

Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy AMOS – AMOS 08
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
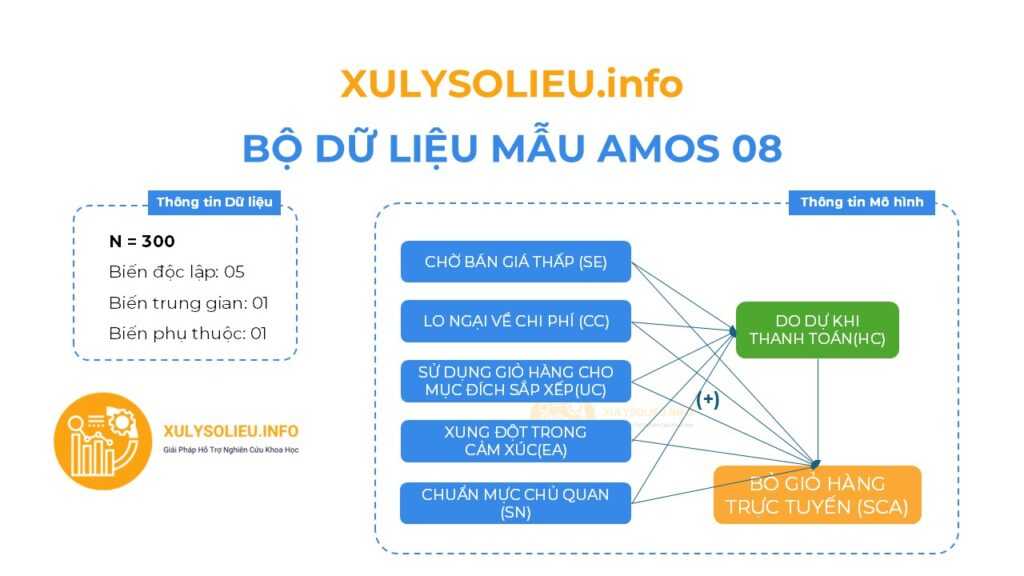
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 300
- Mô hình nghiên cứu bao gồm 07 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (thang đo Likert 5)
- Biến độc lập:
+ CHỜ BÁN GIÁ THẤP (SE): 3 items
+ LO NGẠI VỀ CHI PHÍ (CC): 3 items
+ SỬ DỤNG GIỎ HÀNG CHO MỤC ĐÍCH SẮP XẾP (UC): 3 items
+ XUNG ĐỘT TRONG CẢM XÚC (EA): 4 items
+ CHUẨN MỰC CHỦ QUAN (SN): 6 items - Biến trung gian: DO DỰ KHI THANH TOÁN (HC): 5 items
- Biến phụ thuộc: BỎ GIỎ HÀNG TRỰC TUYẾN (SCA): 4 items
2. Chi tiết kết quả kiểm định
- Output File từ gói Dữ Liệu Mẫu:
+ File dữ liệu excel
+ File văn bản kết quả
+ File kết quả xử lý từ phần mềm - Link xem trước kết quả dữ liệu mẫu: Tại đây!
Giá gốc: 499k VND- Giá ưu đãi: 268k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI

Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy AMOS – AMOS 06
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
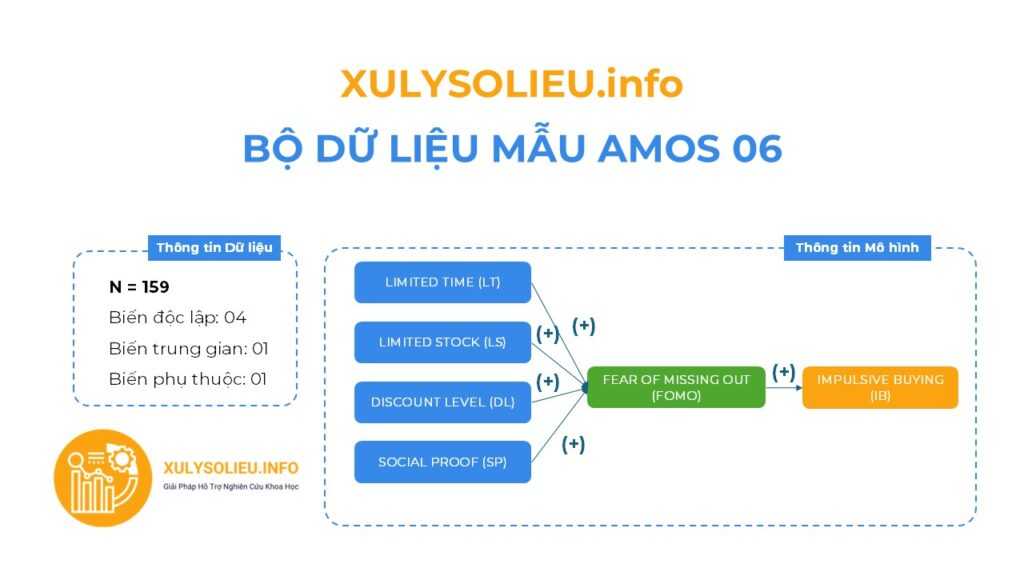
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 159
- Mô hình nghiên cứu bao gồm 06 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (thang đo Likert 5)
- Biến độc lập: 04
+ LIMITED TIME (LT): 4 items
+ LIMITED STOCK (LS): 4 items
+ DISCOUNT LEVEL (DL): 4 items
+ SOCIAL PROOF (SP): 4 items - Biến trung gian: 01
+ FEAR OF MISSING OUT (FOMO): 4 items - Biến phụ thuộc: 01
+ IMPULSIVE BUYING (IB): 6 items
2. Chi tiết kết quả kiểm định
- Output File từ gói Dữ Liệu Mẫu:
+ File dữ liệu excel
+ File văn bản kết quả
+ File kết quả xử lý từ phần mềm - Link xem trước kết quả dữ liệu mẫu: Tại đây!
Giá gốc: 499k VND- Giá ưu đãi: 268k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI

Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
Two-Way ANOVA trong SPSS: Cách thực hiện & Diễn giải kết quả chi tiết nhất
Two-Way ANOVA (Phân tích phương sai hai yếu tố) là một công cụ mạnh mẽ giúp các nhà nghiên cứu đánh giá sự ảnh hưởng của hai biến định tính đến một biến định lượng. Nếu bạn muốn so sánh sự khác biệt về một biến định lượng, chẳng hạn như sự hài lòng công việc, giữa các nhóm có sự phân loại theo hai yếu tố, Two-Way ANOVA sẽ là phương pháp phù hợp. Trong bài viết này, chúng ta sẽ tìm hiểu cách thực hiện và diễn giải kết quả của kiểm định ANOVA hai nhân tố trong SPSS, từ cách thực hiện đến cách đọc kết quả một cách chi tiết và dễ hiểu.
1. Two-Way ANOVA là gì?
Phân tích Two-Way ANOVA giúp kiểm tra sự ảnh hưởng đồng thời của hai biến định tính (yếu tố) đến một biến định lượng. Ví dụ, nếu bạn muốn kiểm tra xem sự hài lòng công việc có sự khác biệt giữa các nhóm nhân viên có giới tính khác nhau và thâm niên làm việc khác nhau, bạn sẽ sử dụng kiểm định Two-Way ANOVA. Phương pháp này không chỉ kiểm tra ảnh hưởng của từng yếu tố mà còn xem xét sự tương tác giữa hai yếu tố này.
2. Cách thực hiện Two-Way ANOVA trong SPSS
Bước 1: Chuẩn bị dữ liệu
Giả sử bạn có một bộ dữ liệu của 350 nhân viên tại công ty, với ba biến:
- F_HL: Mức độ hài lòng công việc (biến định lượng).
- GioiTinh: Giới tính nhân viên (biến định tính).
- ThamNien: Thâm niên làm việc (biến định tính).
Bước 2: Chạy kiểm định Two-Way ANOVA trong SPSS
1. Mở SPSS và chọn Analyze > General Linear Model > Univariate.
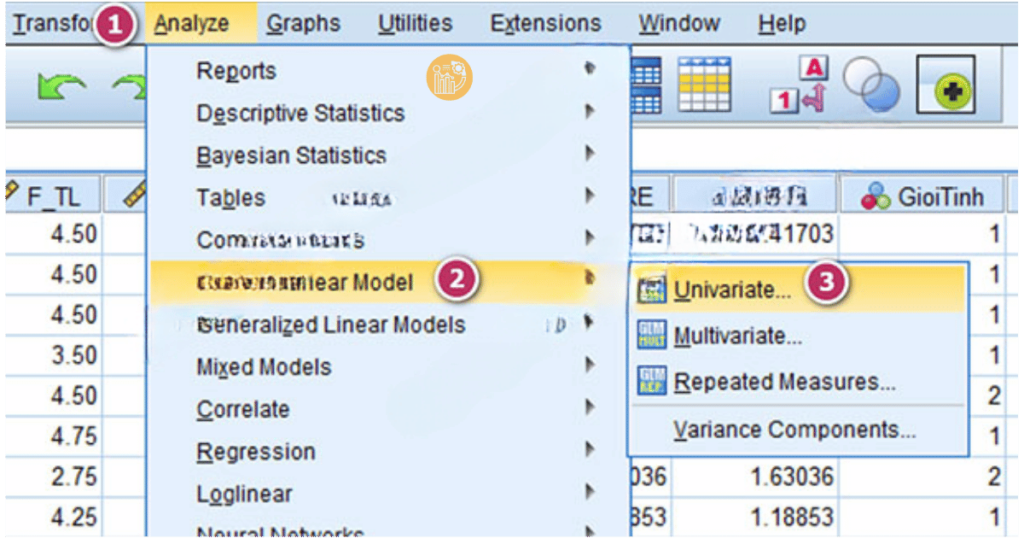
2. Trong cửa sổ Univariate, đưa biến F_HL vào ô Dependent Variable.
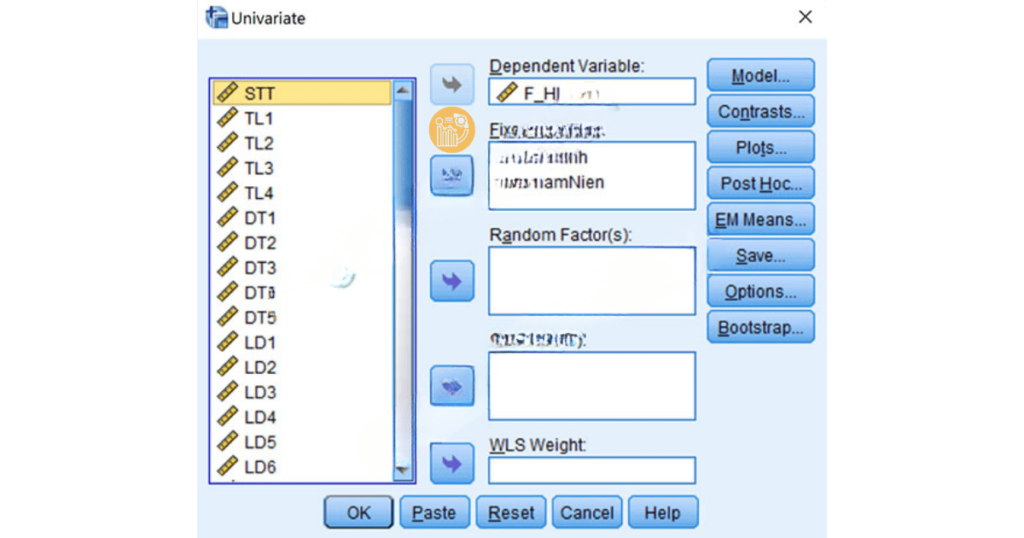
3. Đưa các biến GioiTinh và ThamNien vào ô Fixed Factor(s).
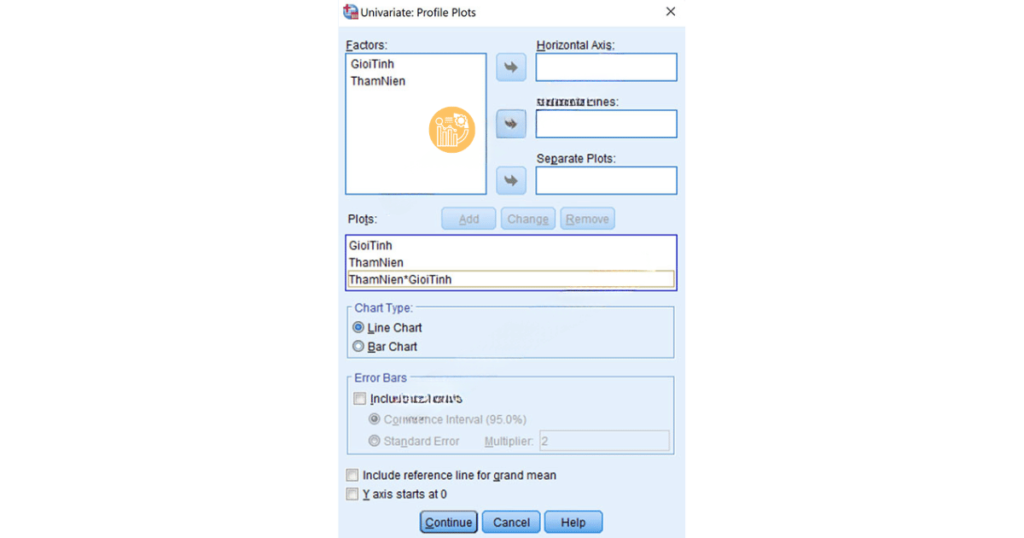
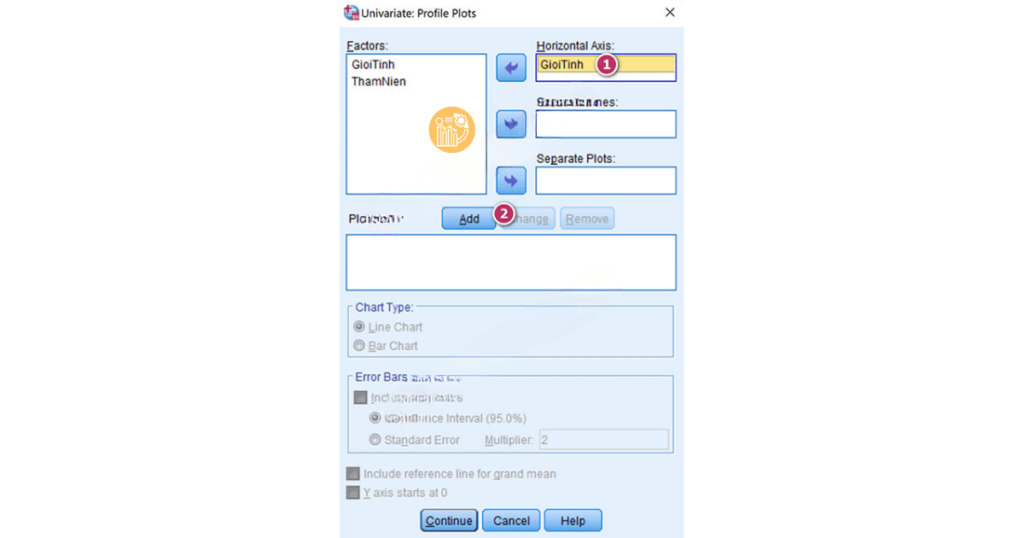
4. Nhấn Plots và thêm các biến định tính vào các mục Horizontal Axis và Separate Lines để tạo đồ thị biểu diễn mối quan hệ giữa biến F_HL và hai yếu tố GioiTinh và ThamNien.
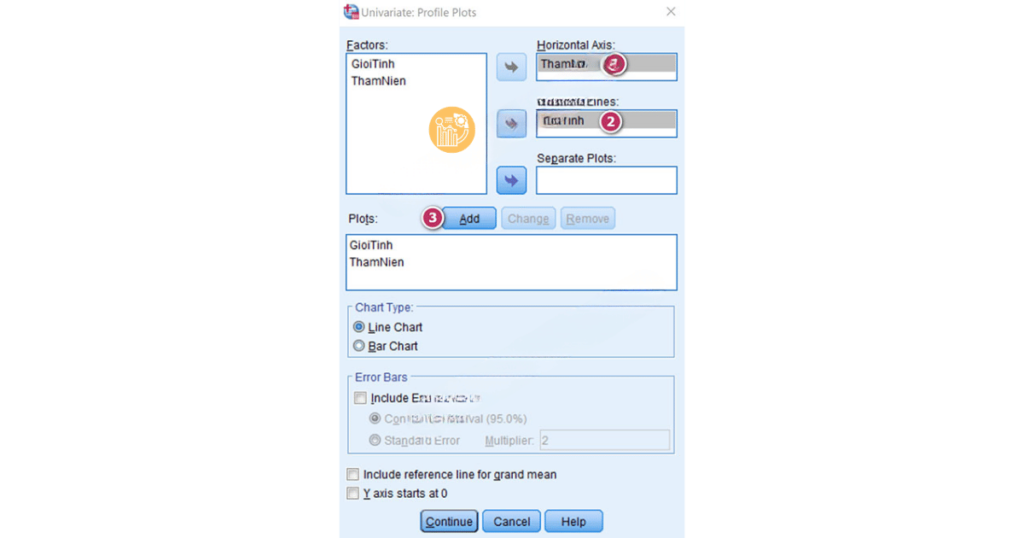
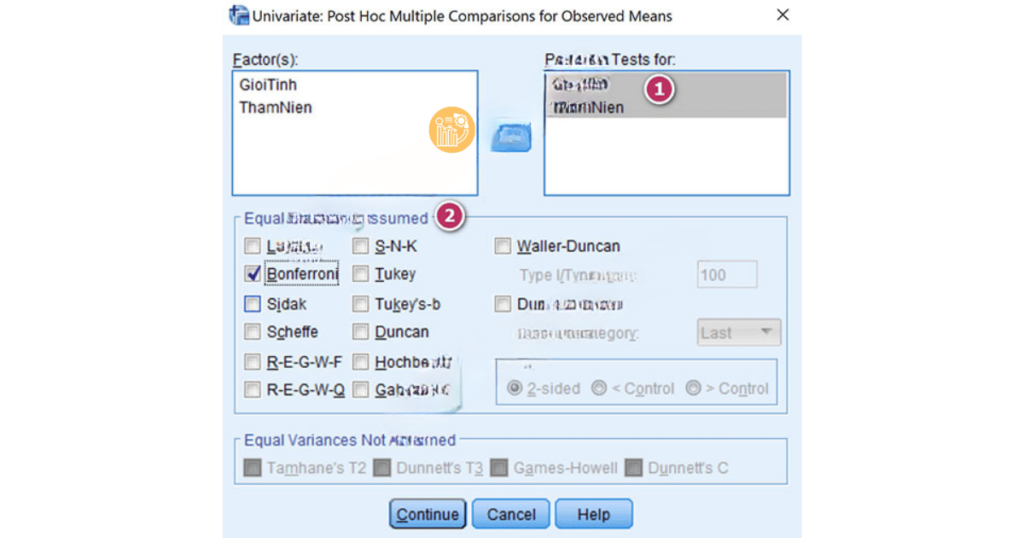
5. Chọn Post Hoc để thực hiện phân tích sâu nếu có sự khác biệt giữa các nhóm trong mỗi yếu tố (ví dụ: LSD hoặc Bonferroni).
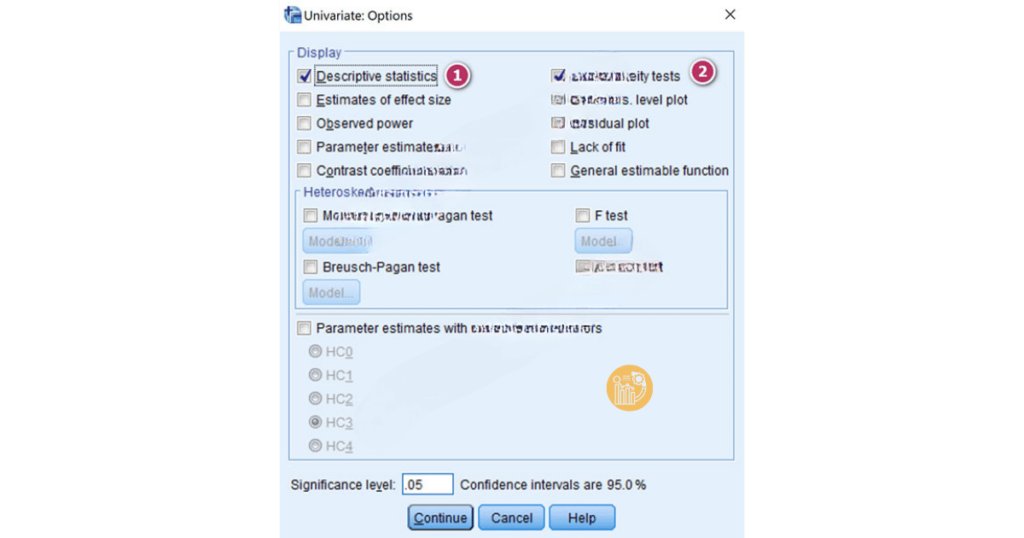
6. Trong mục Options, chọn Descriptive statistics và Homogeneity tests để hiển thị các kết quả mô tả và kiểm tra giả thuyết về phương sai. Nhấn OK để xuất kết quả ra output.
3. Cách đọc kết quả Two-Way ANOVA trong SPSS
Bước 1: Kiểm tra phương sai sai số (Levene’s Test)
Bảng Levene’s Test of Equality of Error Variances sẽ cho bạn kết quả kiểm tra giả thuyết về sự đồng đều phương sai giữa các nhóm.
- Nếu sig lớn hơn 0.05, có thể tiếp tục đọc kết quả phân tích ANOVA.
- Nếu sig nhỏ hơn 0.05, kết quả phân tích ANOVA không chính xác và bạn nên dừng lại.
Bước 2: Xem kết quả của Tests of Between-Subjects Effects
Bảng này sẽ cho bạn kết quả kiểm tra sự khác biệt trung bình giữa các nhóm trong các yếu tố GioiTinh, ThamNien và sự tương tác giữa chúng.
- GioiTinh: Nếu sig lớn hơn 0.05, không có sự khác biệt hài lòng giữa nhân viên nam và nữ.
- ThamNien: Nếu sig nhỏ hơn 0.05, có sự khác biệt hài lòng giữa các nhóm thâm niên làm việc khác nhau.
- GioiTinh * ThamNien (Interaction): Nếu sig nhỏ hơn 0.05, sự tương tác giữa giới tính và thâm niên có ảnh hưởng đến sự hài lòng công việc.
Bước 3: Phân tích sâu (Post Hoc Tests)
Với sự khác biệt giữa các nhóm, SPSS sẽ cung cấp phân tích sâu hơn ở bảng Post Hoc Test để xác định chính xác nhóm nào khác biệt với nhóm còn lại.
Bước 4: Đọc đồ thị
Biểu đồ giúp bạn dễ dàng quan sát sự khác biệt giữa các nhóm. Ví dụ, bạn có thể thấy rằng với nhân viên nam, sự hài lòng công việc có xu hướng tăng khi thâm niên tăng, trong khi nhân viên nữ không có sự thay đổi đáng kể theo thâm niên.
4. Kết luận từ kết quả Two-Way ANOVA

Dựa vào kết quả kiểm định Two-Way ANOVA, bạn có thể rút ra những kết luận quan trọng về mối quan hệ giữa các yếu tố. Nếu kết quả cho thấy có sự tương tác giữa hai yếu tố, điều đó có nghĩa là tác động của một yếu tố lên biến định lượng sẽ thay đổi tùy thuộc vào mức độ của yếu tố còn lại.
Ví dụ, nếu bạn nhận thấy rằng thâm niên làm việc có ảnh hưởng mạnh mẽ đến sự hài lòng công việc của nhân viên nam nhưng không ảnh hưởng nhiều đến nhân viên nữ, bạn có thể cần điều chỉnh các chính sách quản lý nhân sự cho phù hợp với đặc điểm này.
5. Tóm tắt
- Two-Way ANOVA giúp kiểm tra sự ảnh hưởng của hai yếu tố định tính đến một biến định lượng và mối quan hệ giữa chúng.
- Để thực hiện kiểm định này trong SPSS, bạn cần chọn các yếu tố và biến thích hợp, sau đó phân tích kết quả qua các bảng kiểm tra phương sai và các hiệu ứng giữa các yếu tố.
- Đọc kết quả cẩn thận để hiểu các sự khác biệt giữa các nhóm và sự tương tác giữa các yếu tố.
Với những kiến thức này, bạn sẽ có thể thực hiện phân tích Two-Way ANOVA trong SPSS và hiểu rõ hơn về cách nó ảnh hưởng đến các yếu tố trong nghiên cứu của mình. Nếu bạn gặp khó khăn, đừng ngần ngại tham khảo dịch vụ hỗ trợ phân tích dữ liệu từ [xulysolieu.info] để được trợ giúp chuyên nghiệp.
Exploratory Factor Analysis SPSS: Hướng dẫn chi tiết phân tích nhân tố khám phá (EFA) trong SPSS
Giới thiệu
Exploratory Factor Analysis SPSS – phân tích nhân tố khám phá (EFA) là một kỹ thuật thống kê mạnh mẽ giúp xác định các mối quan hệ tiềm ẩn giữa một tập hợp các biến. Trong nghiên cứu, EFA thường được sử dụng ở giai đoạn đầu để khám phá cấu trúc ẩn trong dữ liệu, giúp đơn giản hóa bộ dữ liệu phức tạp bằng cách nhóm các biến có tương quan với nhau thành các nhân tố. Việc giảm số lượng biến xuống còn một vài nhân tố giúp các nhà nghiên cứu hiểu rõ hơn về cấu trúc dữ liệu và xây dựng các mô hình dễ quản lý và có thể giải thích được.
Bài viết này sẽ hướng dẫn bạn qua các bước cơ bản trong việc thực hiện EFA bằng SPSS, từ việc hiểu các khái niệm cơ bản đến cách giải thích và báo cáo kết quả. Dù bạn là một nhà nghiên cứu mới bắt đầu hay một nhà phân tích dày dặn kinh nghiệm, việc làm chủ EFA trong SPSS sẽ giúp nâng cao chất lượng và độ rõ ràng của các phát hiện nghiên cứu của bạn.
Phân tích nhân tố khám phá (EFA) là gì?
Phân tích nhân tố khám phá (Exploratory Factor Analysis – EFA) là một phương pháp thống kê nhằm khám phá cấu trúc ẩn của một bộ biến quan sát. EFA được sử dụng chủ yếu trong giai đoạn đầu của nghiên cứu để xác định các nhân tố tiềm ẩn (latent variables) ảnh hưởng đến các phép đo quan sát. Các nhà nghiên cứu áp dụng EFA để phát hiện các mô hình giữa các biến, giảm chiều dữ liệu và tạo ra giả thuyết về các mối quan hệ tiềm ẩn giữa các biến.
Khác với các kỹ thuật phân tích nhân tố khác, EFA cho phép khám phá dữ liệu mà không yêu cầu có giả thuyết trước về số lượng hoặc bản chất của các nhân tố. Điều này làm cho EFA đặc biệt hữu ích khi nghiên cứu các lĩnh vực mới hoặc khi nhà nghiên cứu chưa có nhiều kiến thức trước đó về cấu trúc dữ liệu. Việc làm chủ EFA bao gồm hiểu các giả định, ứng dụng và cách giải thích kết quả để khám phá các chiều hướng tiềm ẩn trong bộ dữ liệu phức tạp.
Các phương pháp của EFA
EFA sử dụng nhiều phương pháp khác nhau để xác định cấu trúc nhân tố ẩn trong bộ dữ liệu. Các phương pháp này khác nhau về cách thức trích xuất nhân tố và xử lý biến thiên trong dữ liệu. Dưới đây là một số phương pháp chính được sử dụng trong EFA:
- Principal Component Analysis (PCA): PCA biến đổi các biến ban đầu thành một tập hợp các biến không tương quan gọi là các thành phần chính, giải thích biến thiên tối đa trong dữ liệu.
- Principal Axis Factoring (PAF): PAF tập trung vào việc xác định cấu trúc nhân tố ẩn bằng cách phân tích sự chia sẻ biến thiên giữa các biến, loại bỏ biến thiên riêng biệt.
- Maximum Likelihood (ML): Phương pháp ML ước lượng tải nhân tố và biến thiên riêng biệt bằng cách tối đa hóa khả năng xảy ra của dữ liệu quan sát, giả sử phân phối chuẩn đa biến.
- Alpha Factoring: Phương pháp này đánh giá độ tin cậy của các nhân tố bằng cách xem xét tính đồng nhất của các biến và tối đa hóa hệ số độ tin cậy alpha.
- Image Factoring: Phương pháp này phân tích sự tương quan riêng phần giữa các biến, tập trung vào biến thiên chung và bỏ qua biến thiên riêng.
Quay (Rotation) trong Phân tích Nhân tố Khám phá
Quay trong EFA là một kỹ thuật dùng để cải thiện khả năng giải thích các nhân tố bằng cách làm đơn giản hóa cấu trúc nhân tố. Bằng cách quay các trục nhân tố, các nhà nghiên cứu có thể đạt được một mô hình tải nhân tố rõ ràng và dễ hiểu hơn. Các phương pháp quay khác nhau có các mục đích sử dụng khác nhau:
- Varimax: Phương pháp quay trực giao tối đa hóa phương sai của các tải nhân tố trên mỗi nhân tố, giúp việc giải thích dễ dàng hơn bằng cách tạo ra các nhân tố có tải cao vào một số ít biến.
- Direct Oblimin: Phương pháp quay xiên cho phép các nhân tố có thể tương quan với nhau, cung cấp một sự đại diện thực tế hơn về dữ liệu khi các nhân tố có sự liên quan với nhau.
- Quartimax: Phương pháp quay trực giao đơn giản hóa các cột trong ma trận tải nhân tố, giúp tải biến mạnh vào một nhân tố duy nhất.
- Equamax: Là sự kết hợp của Varimax và Quartimax, phương pháp quay trực giao này cân bằng việc đơn giản hóa các hàng và cột trong ma trận tải nhân tố.
- Promax: Phương pháp quay xiên bắt đầu với giải pháp Varimax và sau đó cho phép các nhân tố có thể tương quan, cung cấp một giải pháp dễ hiểu hơn khi các nhân tố có sự tương quan.
Hệ số tải nhân tố và Biểu đồ Scree
Hệ số tải nhân tố cho biết mức độ tương quan giữa một biến quan sát và một nhân tố. Các hệ số tải nhân tố càng cao cho thấy mối liên hệ mạnh mẽ giữa biến quan sát và nhân tố đó, giúp hiểu rõ hơn về các cấu trúc ẩn trong dữ liệu. Các giá trị hệ số tải nhân tố dao động từ -1 đến 1, với các giá trị gần 1 hoặc -1 chỉ ra mối quan hệ mạnh mẽ.
Biểu đồ Scree là một đại diện đồ họa của các giá trị eigenvalue liên quan đến mỗi nhân tố. Nó giúp xác định số lượng nhân tố cần giữ lại bằng cách chỉ ra điểm mà các eigenvalue bắt đầu ổn định, thường được gọi là “điểm khuỷu” (elbow).
Sự khác biệt giữa EFA và CFA trong SPSS
Phân tích nhân tố khám phá (EFA) và Phân tích nhân tố khẳng định (CFA) phục vụ những mục đích khác nhau trong phân tích thống kê. EFA được sử dụng để khám phá cấu trúc ẩn của dữ liệu mà không có giả thuyết trước, làm cho nó lý tưởng trong các giai đoạn ban đầu của nghiên cứu. EFA giúp xác định các nhân tố tiềm ẩn và thiết lập một hiểu biết cơ bản về mối quan hệ giữa các biến, cho phép tiếp cận linh hoạt và dựa trên dữ liệu.
Ngược lại, CFA kiểm tra các giả thuyết cụ thể hoặc lý thuyết về cấu trúc của dữ liệu. CFA yêu cầu nhà nghiên cứu chỉ định số lượng nhân tố và các biến tải vào từng nhân tố trước. Phương pháp này đánh giá độ phù hợp của mô hình giả thuyết với dữ liệu quan sát, cung cấp một kiểm tra nghiêm ngặt các cấu trúc lý thuyết.
Các giả định của Phân tích Nhân tố Khám phá
- Tính tuyến tính: Mối quan hệ giữa các biến phải là tuyến tính.
- Tính chuẩn: Dữ liệu nên tuân theo phân phối chuẩn đa biến.
- Kích thước mẫu đầy đủ: Cần có số lượng quan sát đủ lớn, thường ít nhất từ 5 đến 10 lần số biến.
- Không có đa cộng tuyến hoàn hảo: Các biến không nên có sự tương quan hoàn hảo với nhau.
- Tính đồng nhất (Homoscedasticity): Phương sai sai số nên đồng nhất trên tất cả các mức độ của các biến.
- Tính cầu (Sphericity): Ma trận tương quan phải khác biệt đáng kể so với ma trận đơn vị, chỉ ra rằng các biến có mối quan hệ đủ mạnh để nhóm lại thành các nhân tố.
Ví dụ efa
Giả sử bạn muốn nghiên cứu các yếu tố ảnh hưởng đến sự hài lòng của sinh viên đối với trải nghiệm đại học của họ. Các nhà nghiên cứu thiết kế một bảng câu hỏi với 10 câu hỏi, bao phủ các khía cạnh như chất lượng học thuật, cơ sở vật chất, đời sống xã hội và dịch vụ hỗ trợ. Để khám phá các nhân tố tiềm ẩn, họ quyết định thực hiện phân tích nhân tố khám phá (EFA) sử dụng SPSS.
Hướng dẫn cách chạy EFA trong SPSS
Bước 1: Mở dữ liệu trong SPSS, đảm bảo rằng dữ liệu bao gồm các biến bạn muốn phân tích.
Bước 2: Vào menu Analyze > Dimension Reduction > Factor để mở hộp thoại phân tích nhân tố.
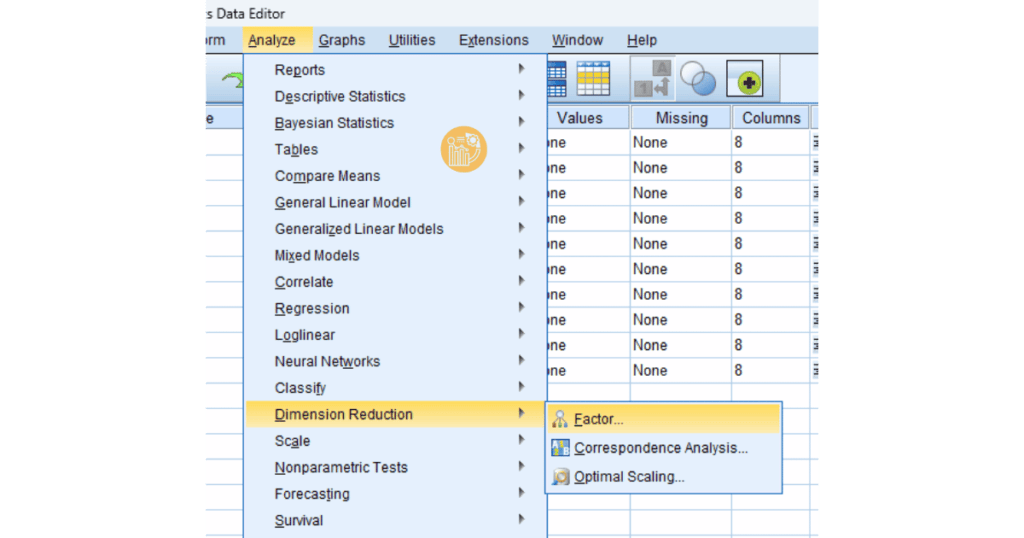
Bước 3: Chọn các biến muốn bao gồm trong phân tích và di chuyển chúng vào hộp Variables.
Bước 4: Nhấp vào nút Extraction, chọn phương pháp trích xuất như PCA hoặc PAF và xác định số lượng nhân tố cần trích xuất.
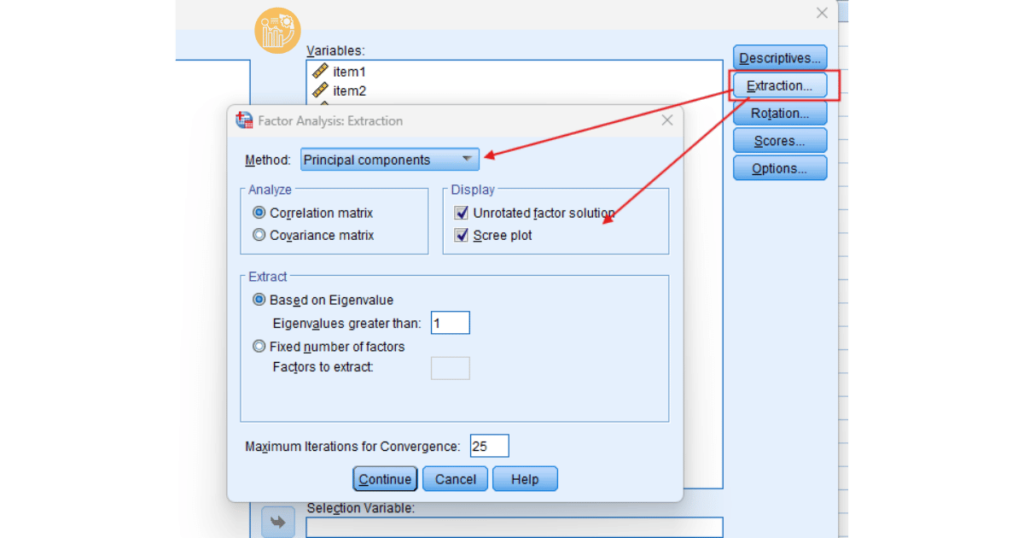
Bước 5: Áp dụng quay, chọn phương pháp quay như Varimax hoặc Direct Oblimin để làm rõ cấu trúc nhân tố.
Bước 6: Nhấn OK để chạy phân tích. SPSS sẽ tạo ra các bảng kết quả bao gồm tải nhân tố, eigenvalue và phương sai giải thích.
Kết luận
Phân tích nhân tố khám phá (EFA) trong SPSS là công cụ mạnh mẽ giúp các nhà nghiên cứu khai thác các yếu tố tiềm ẩn trong dữ liệu. Bằng cách hiểu và thực hiện EFA, bạn có thể xây dựng các mô hình dễ hiểu và dễ giải thích. Nếu bạn cần thêm hỗ trợ trong việc xử lý dữ liệu, hãy tham khảo dịch vụ phân tích dữ liệu SPSS tại xulysolieu.info để nhận kết quả chính xác và hiệu quả.
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy AMOS – AMOS 07
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
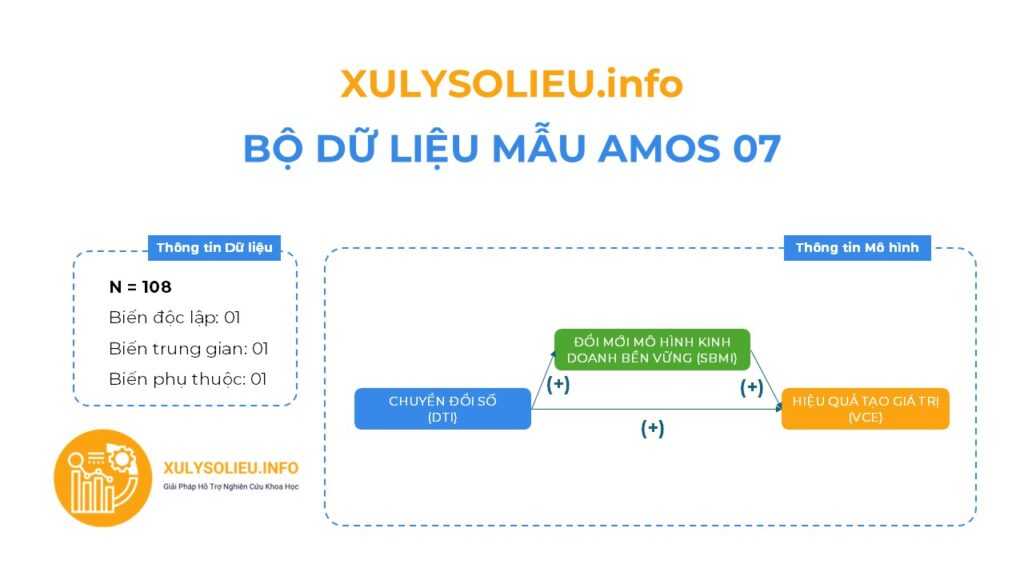
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 108
- Mô hình nghiên cứu bao gồm 03 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (thang đo Likert 5)
- Biến độc lập: 01
+ Chuyển đổi số (DTI) – 6 items - Biến trung gian: 01
+ Đổi mới mô hình kinh doanh bền vững (SBMI) – 4 items - Biến phụ thuộc: 01
+ Hiệu quả tạo giá trị (VCE) – 4 items***Theo lý thuyết mô hình bài mẫu:
+ Biến độc lập – Chuyển đổi số (DTI): gồm 4 thành phần (hạ tầng CNTT, nhân lực số, ứng dụng số, dịch vụ trực tuyến).
+ Biến trung gian – Đổi mới mô hình kinh doanh bền vững (SBMI): gồm 3 thành phần (kinh tế, xã hội, môi trường).
+ Biến phụ thuộc – Hiệu quả tạo giá trị (VCE): gồm 3 chỉ số (lợi nhuận tài chính, sự hài lòng khách hàng, tác động xã hội – môi trường).
+ Biến kiểm soát: quy mô doanh nghiệp, vốn chủ sở hữu, tuổi đời doanh nghiệp.
2. Chi tiết kết quả kiểm định
- Output File từ gói Dữ Liệu Mẫu:
+ File dữ liệu excel
+ File văn bản kết quả
+ File kết quả xử lý từ phần mềm - Link xem trước kết quả dữ liệu mẫu: Tại đây!
Giá gốc: 499k VND- Giá ưu đãi: 268k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI

Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-amos/
Hệ số Durbin Watson trong hồi quy: Cách tính, bảng tra hai mức giá trị Alpha 0.1 và Alpha 0.6 & Cách xử lý tự tương quan
Hệ số Durbin Watson là gì?
Hệ số Durbin Watson (DW) là một đại lượng thống kê được sử dụng để kiểm tra sự tự tương quan chuỗi bậc nhất giữa các phần dư trong mô hình hồi quy. Chỉ số DW có giá trị biến thiên từ 0 đến 4:
- DW = 2: Không có sự tự tương quan chuỗi bậc nhất, tức là phần dư không có mối liên hệ.
- DW < 2: Có sự tự tương quan thuận giữa các phần dư (sự tương quan dương).
- DW > 2: Có sự tự tương quan nghịch giữa các phần dư (sự tương quan âm).
Cách tính hệ số Durbin Watson
Hệ số Durbin Watson được tính bằng cách so sánh sự thay đổi giữa các phần dư kề nhau trong mô hình hồi quy. Công thức tính DW như sau:
DW = ∑(e_t - e_{t-1})² / ∑e_t²
Trong đó:
- e_t: phần dư tại thời điểm t.
- e_{t-1}: phần dư tại thời điểm t-1.
- n: số quan sát trong mẫu.
Cách tra bảng Durbin Watson
Để tra cứu giá trị Durbin Watson, bạn cần biết ba yếu tố quan trọng: mức ý nghĩa (α), cỡ mẫu (n), và số biến độc lập tham gia vào hồi quy (k). Sau đây là các bước chi tiết để tra cứu bảng Durbin Watson:
- Chọn mức ý nghĩa (α): Mức ý nghĩa phổ biến thường là 0.01 (1%) hoặc 0.05 (5%). Bạn sẽ chọn mức ý nghĩa phù hợp với nghiên cứu của mình. Trong các nghiên cứu về kinh tế, xã hội, tiếp thị, mức 5% (α = 0.05) thường được sử dụng.
- Xác định cỡ mẫu (n) và số biến độc lập (k): Tìm cỡ mẫu và số biến độc lập trong mô hình hồi quy của bạn.
- Tra cứu bảng Durbin Watson: Sau khi xác định được các giá trị α, n và k, tra cứu bảng Durbin Watson để tìm ra giá trị dL và dU.
- So sánh giá trị DW với bảng tra: Đưa giá trị DW từ phân tích hồi quy so với bảng tra để đưa ra kết luận về sự tự tương quan.
Cách xử lý khi có tự tương quan
Sau khi tra cứu bảng Durbin Watson, bạn sẽ so sánh giá trị DW thu được với các giá trị dL, dU, và 4 – dU. Dưới đây là các kết luận có thể rút ra:
- DW < dL: Có sự tự tương quan bậc nhất, và sự tương quan này là dương (thuận).
- DW > 4 – dL: Có sự tự tương quan bậc nhất, và sự tương quan này là âm (nghịch).
- dL < DW < dU hoặc 4 – dU < DW < 4 – dL: Không thể kết luận được về tự tương quan.
- dU < DW < 4 – dU: Không có sự tự tương quan bậc nhất.
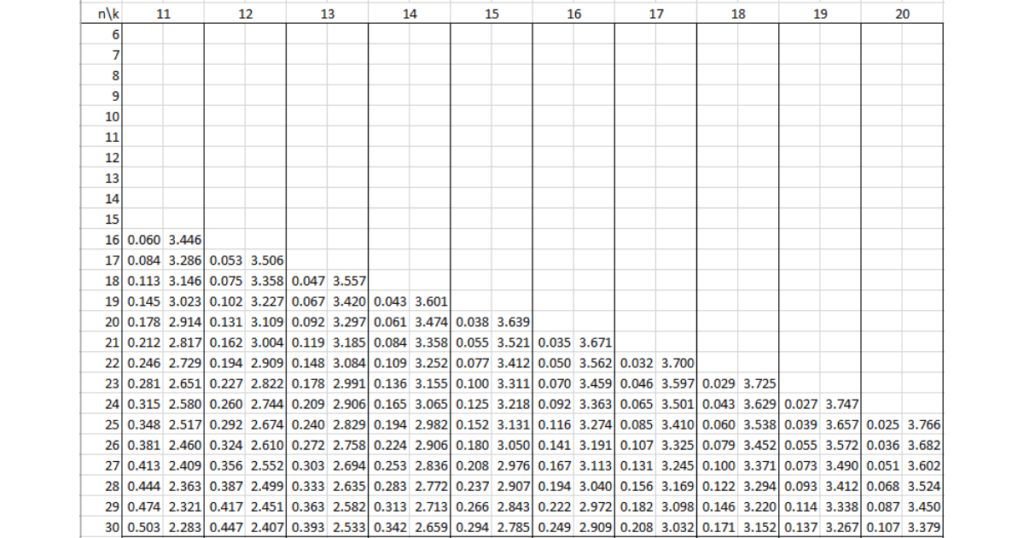
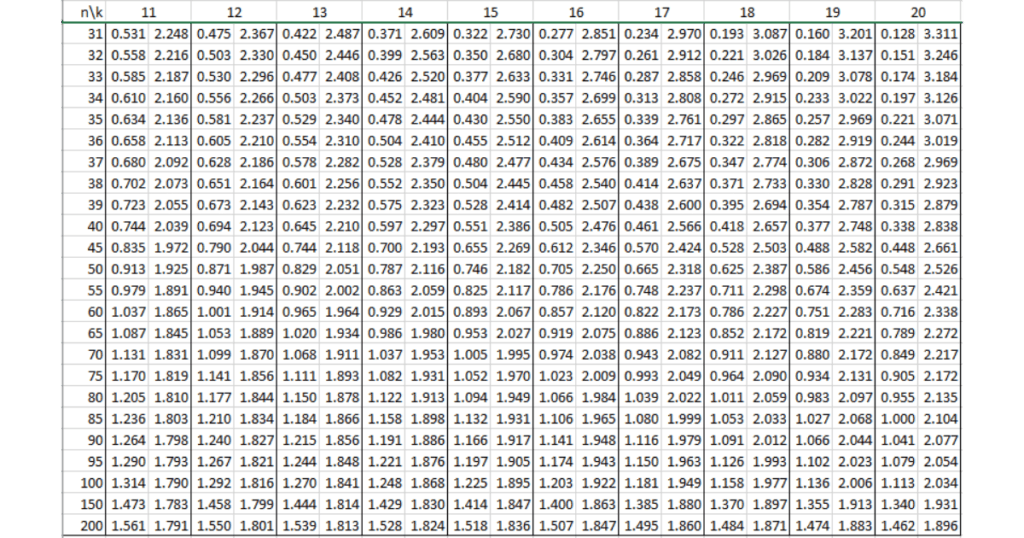
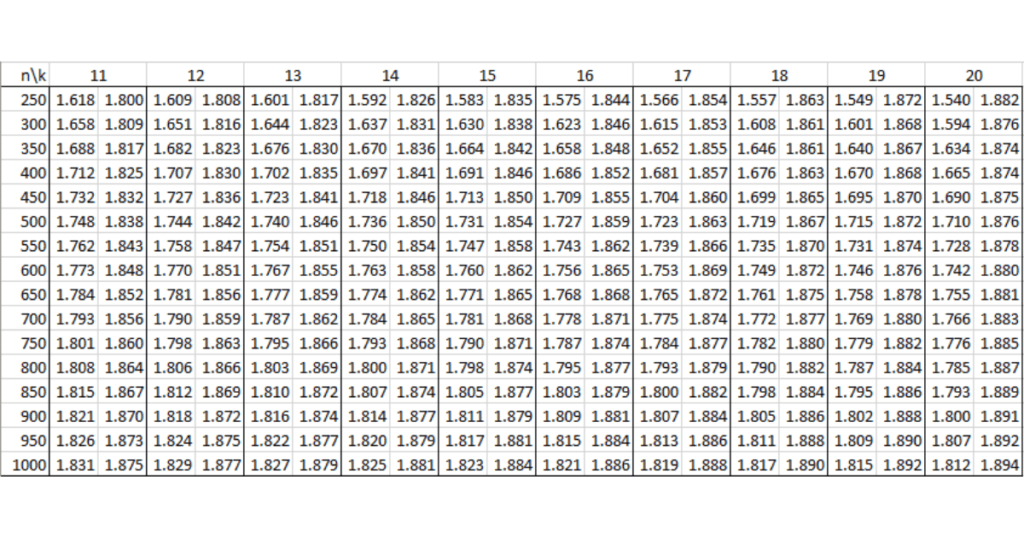
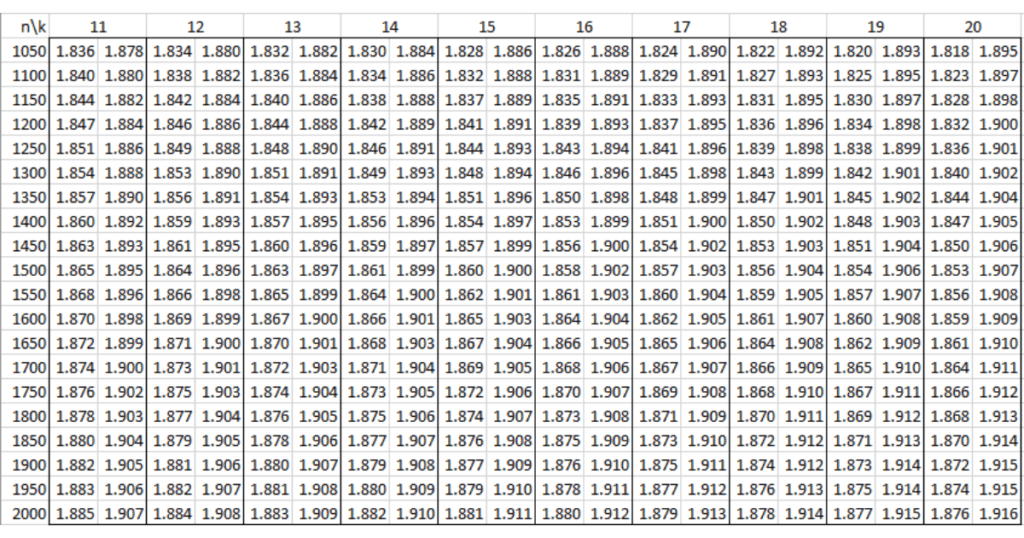
Bảng tra Durbin Watson tại mức ý nghĩa 1% (α = 0.01)
Dưới đây là bảng tra Durbin Watson tại mức ý nghĩa 1% (α = 0.01), giúp bạn đánh giá sự tự tương quan của các phần dư trong hồi quy.
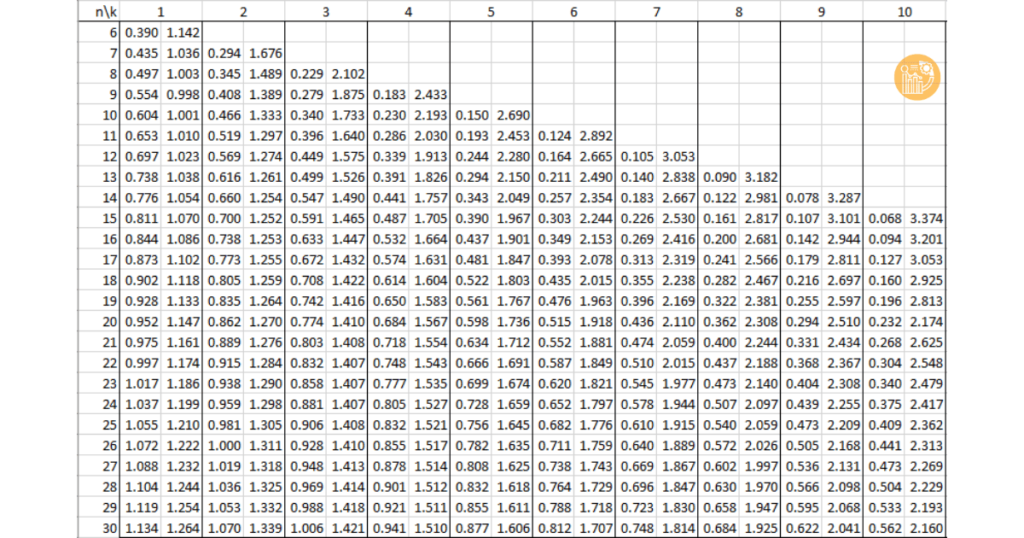
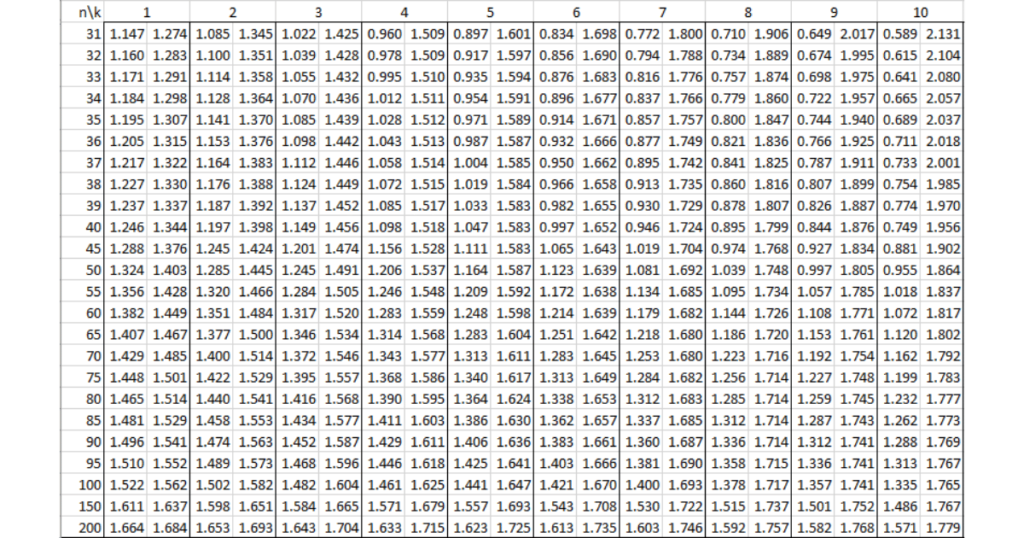
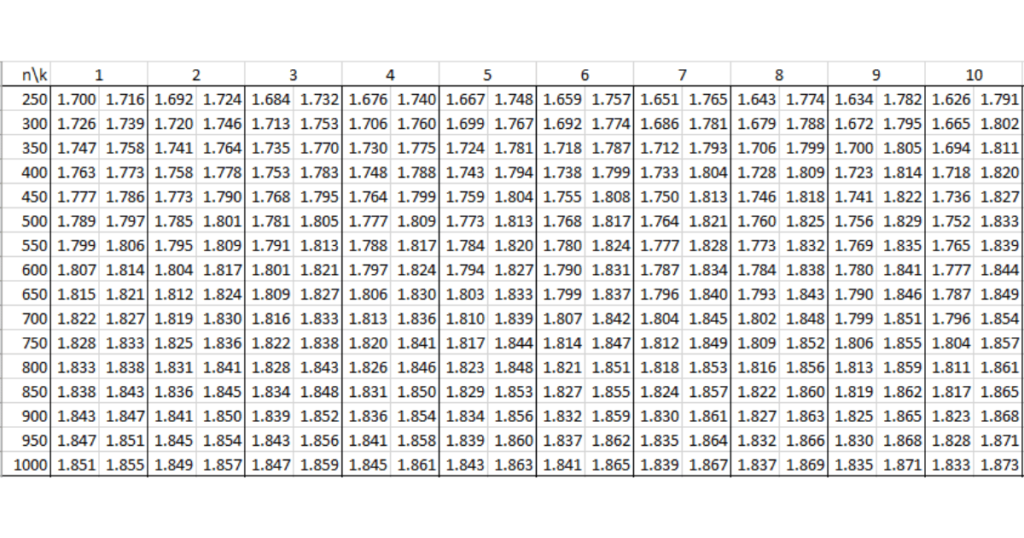
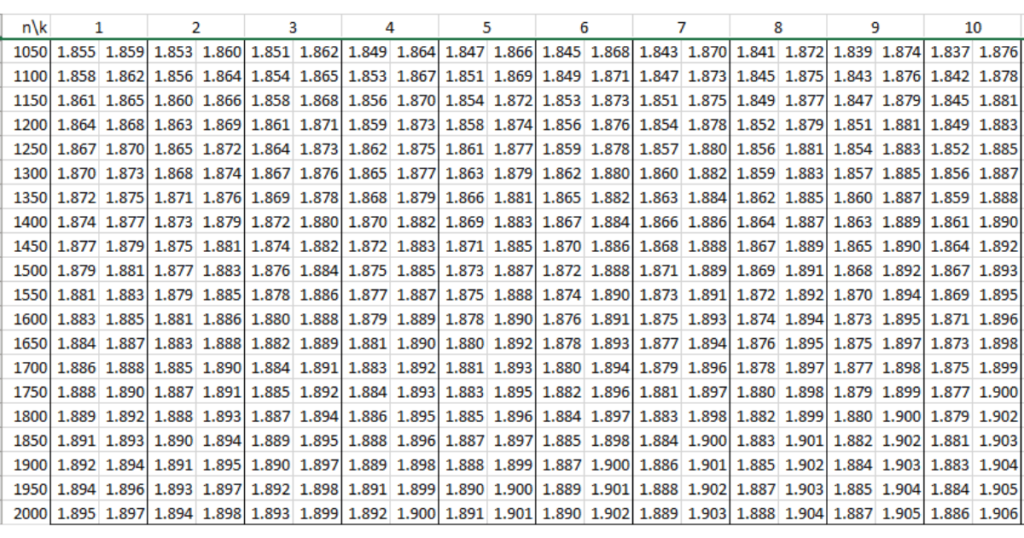
Bảng tra Durbin Watson tại mức ý nghĩa 5% (α = 0.05)
Tương tự, bảng tra Durbin Watson tại mức ý nghĩa 5% giúp bạn có cái nhìn rõ hơn về sự tự tương quan tại mức ý nghĩa thông dụng hơn. Mức ý nghĩa 5% (α = 0.05) thường được sử dụng trong các nghiên cứu thực tế.

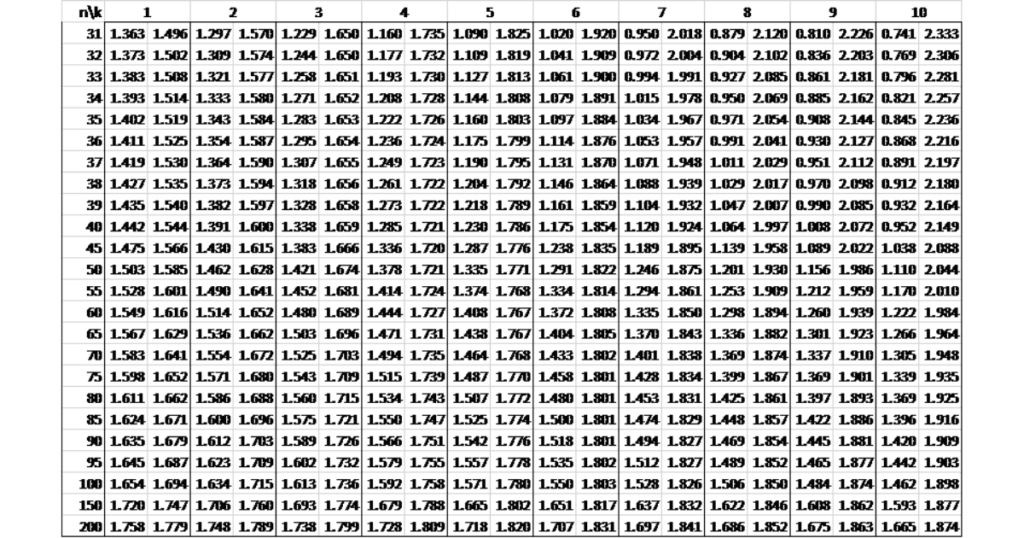
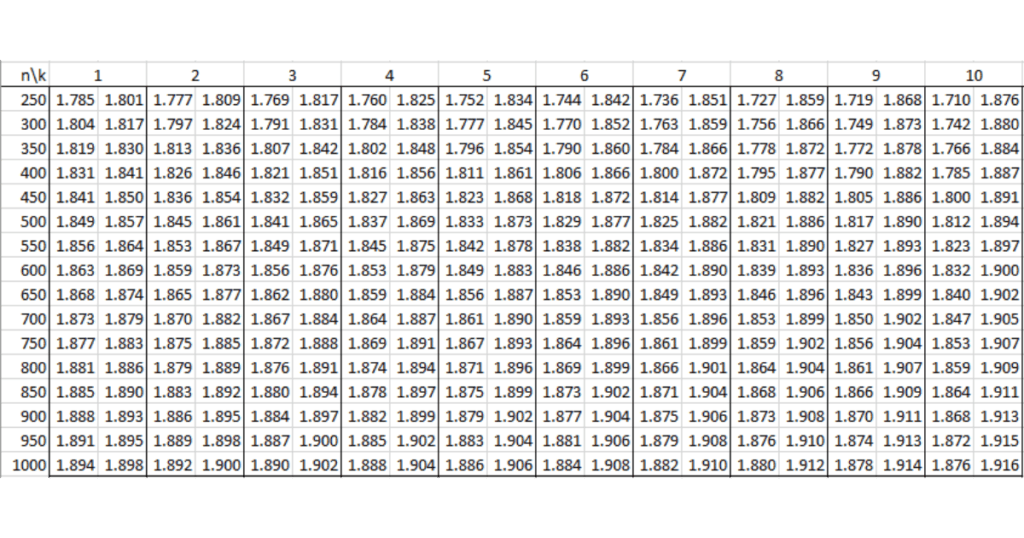
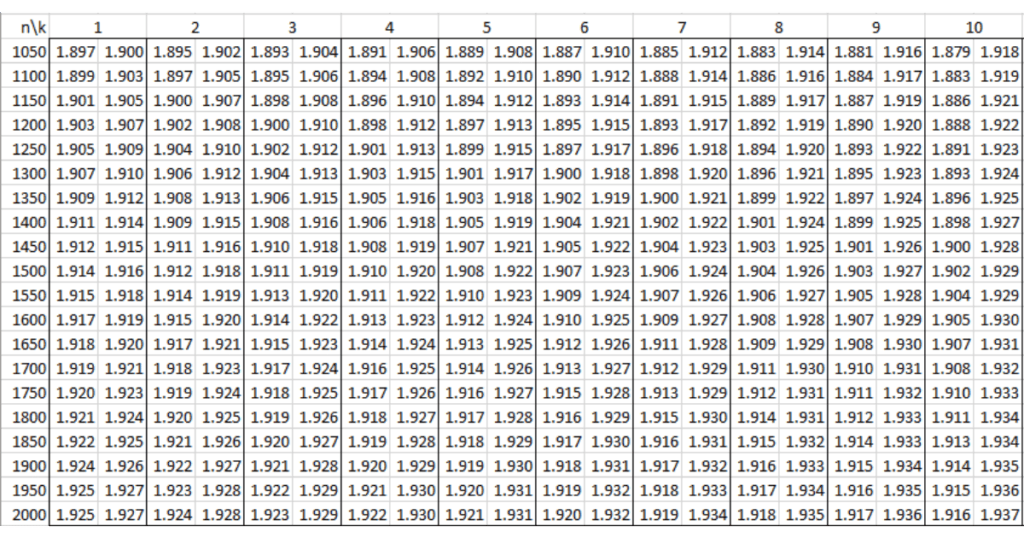
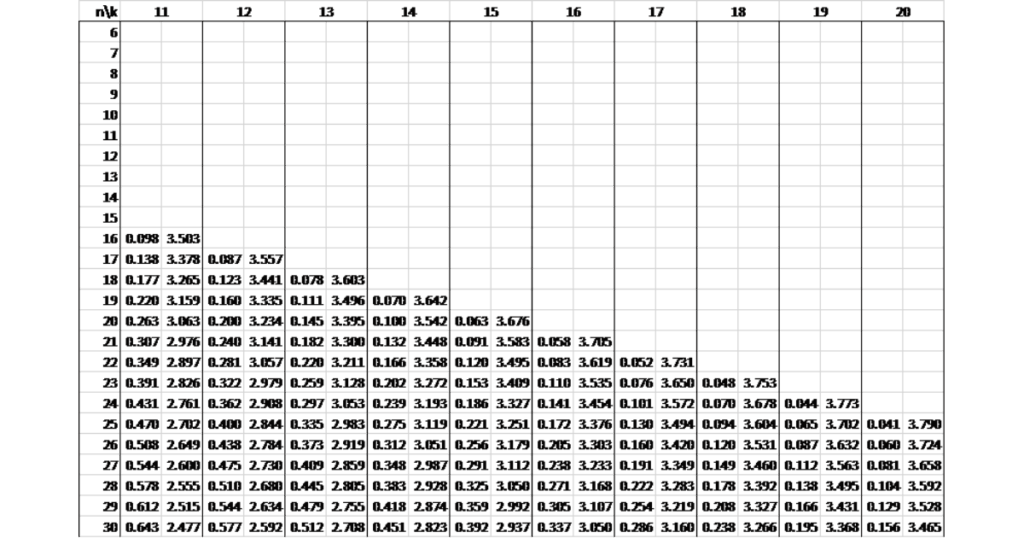
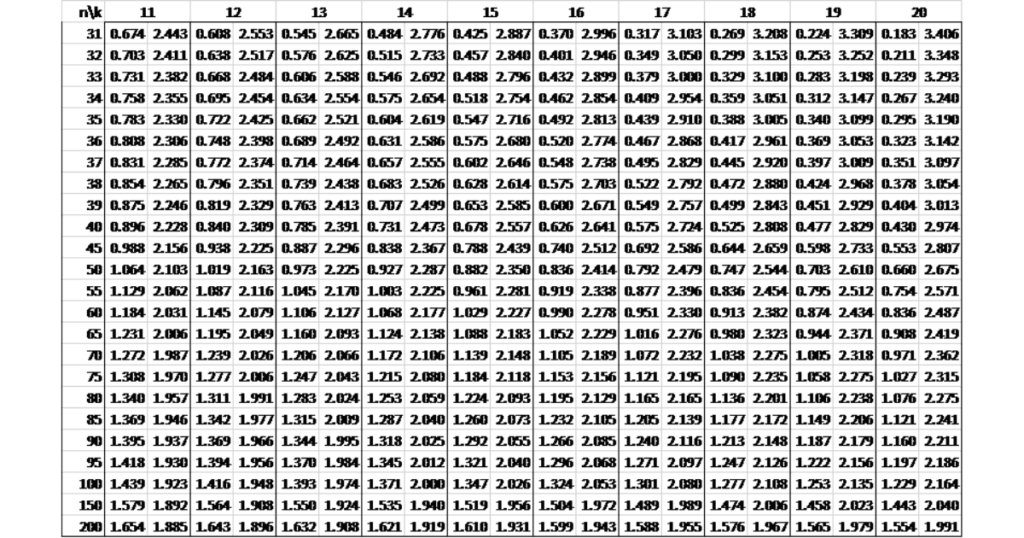
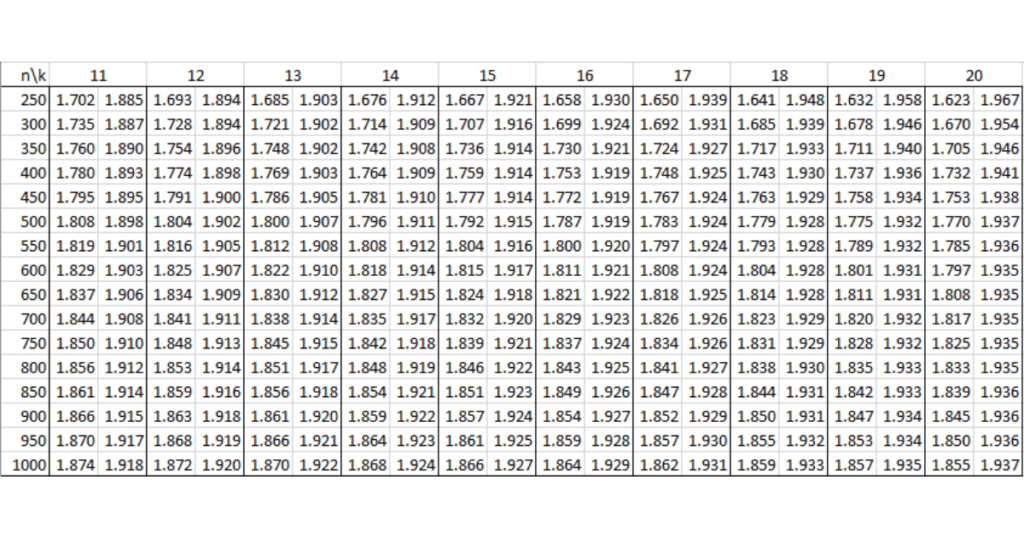
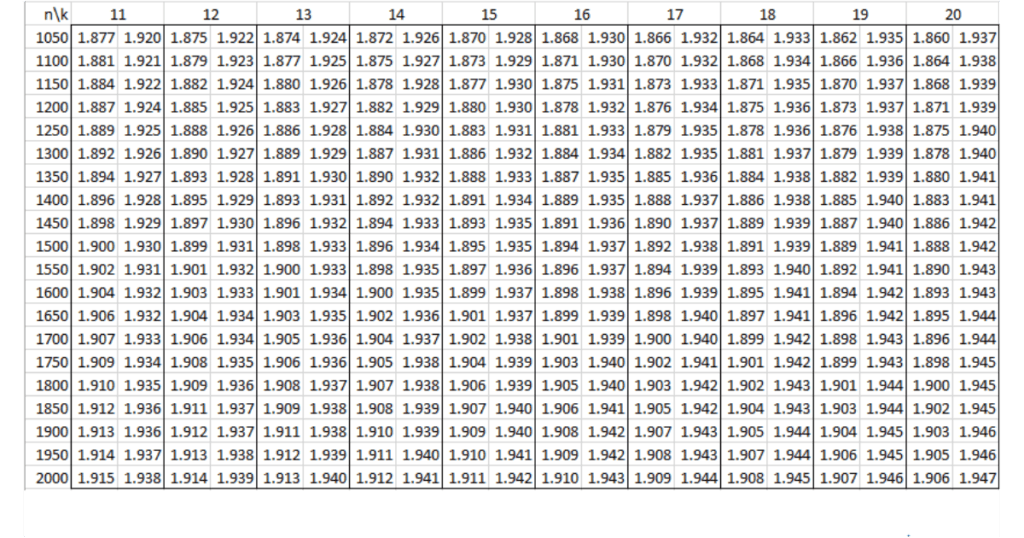
Giá trị Durbin Watson bao nhiêu là tốt?
Giá trị Durbin Watson lý tưởng là 2, cho thấy không có sự tự tương quan giữa các phần dư. Tuy nhiên, giá trị này có thể thay đổi tùy thuộc vào mức độ tự tương quan trong dữ liệu. Một số hướng dẫn cơ bản:
- DW = 2: Không có sự tự tương quan.
- DW < 2: Tự tương quan thuận (dương).
- DW > 2: Tự tương quan nghịch (âm).
Kiểm định tự tương quan Durbin Watson
Kiểm định tự tương quan Durbin Watson là một phần quan trọng trong phân tích hồi quy để đảm bảo rằng các ước lượng từ mô hình là chính xác và có tính dự đoán. Nếu kết quả kiểm định chỉ ra sự tự tương quan trong các phần dư, bạn có thể áp dụng các phương pháp xử lý như thêm các biến giải thích vào mô hình hoặc sử dụng các mô hình hồi quy tự hồi quy (AR) để khắc phục vấn đề này.
Kết luận
Hệ số Durbin Watson là một công cụ mạnh mẽ giúp bạn phát hiện và xử lý sự tự tương quan chuỗi bậc nhất trong mô hình hồi quy. Việc kiểm tra và xử lý tự tương quan giúp cải thiện độ chính xác của mô hình, từ đó đưa ra những kết luận đáng tin cậy hơn. Nếu bạn gặp khó khăn trong việc phân tích và xử lý dữ liệu hồi quy, hãy tham khảo dịch vụ phân tích dữ liệu SPSS từ xulysolieu.info để tối ưu hóa thời gian và có được kết quả chính xác.
Top 5 lỗi khi viết bản thảo người làm nghiên cứu thường gặp
Viết bản thảo là giai đoạn chuyển hóa kết quả nghiên cứu thành tri thức có giá trị, là nơi mọi công sức thu thập dữ liệu, xử lý và phân tích được trình bày một cách logic, thuyết phục và có tính học thuật. Dù bạn làm khóa luận tốt nghiệp, luận văn thạc sĩ hay bài báo khoa học, bản thảo chính là phần thể hiện năng lực nghiên cứu và tư duy khoa học của người viết.
Tuy nhiên, trên thực tế, nhiều sinh viên và nhà nghiên cứu trẻ thường mắc lỗi ngay từ bước viết bản thảo này. Có người thu thập và phân tích dữ liệu rất tốt, nhưng bài viết lại thiếu cấu trúc, diễn đạt cảm tính, hoặc trích dẫn sai chuẩn. Hệ quả là bài nghiên cứu dù có nội dung hay vẫn bị đánh giá thấp, không thể hiện được giá trị khoa học thật sự.
Chính vì vậy, việc viết bản thảo được xem là “bước gỡ điểm” quan trọng – bởi chỉ cần viết đúng cách, bạn có thể cải thiện đáng kể chất lượng bài làm, giúp hội đồng đánh giá dễ dàng nhận thấy tư duy logic, sự đầu tư nghiêm túc và năng lực học thuật của người viết.
Mục tiêu của bài viết này là giúp bạn nhận diện 5 lỗi phổ biến nhất khi viết bản thảo, kèm theo giải pháp cụ thể để tránh những sai sót không đáng có, từ đó nâng cao chất lượng nghiên cứu và thể hiện chuyên nghiệp hơn trong từng trang viết.
Lỗi viết bản thảo #1: Không xác định rõ cấu trúc và logic của bài nghiên cứu
Một trong những lỗi cơ bản và phổ biến nhất mà sinh viên hay mắc phải khi viết bản thảo là không xây dựng cấu trúc rõ ràng trước khi viết bản thảo. Nhiều người viết theo cảm tính, “nghĩ gì viết nấy”, dẫn đến nội dung lan man, thiếu mạch lạc. Bài viết có thể chứa nhiều ý hay, dữ liệu phong phú, nhưng lại không tuân theo bố cục chuẩn của một bài nghiên cứu khoa học, ví dụ:
Mở đầu – Cơ sở lý thuyết – Phương pháp nghiên cứu – Kết quả – Thảo luận – Kết luận
Khi thiếu cấu trúc, bài nghiên cứu giống như một chuỗi thông tin rời rạc, không có sự kết nối logic giữa các phần, khiến người đọc hoặc hội đồng đánh giá khó nắm bắt được mục tiêu, kết quả và đóng góp của công trình.

⚠️ Hậu quả:
- Bài viết mất đi tính khoa học, khiến người đọc phải “tự tìm ý chính”.
- Giảm đáng kể điểm trình bày và tính học thuật dù nội dung nghiên cứu tốt.
- Dễ bị đánh giá là “không hiểu quy trình nghiên cứu chuẩn”.
✅ Giải pháp:
- Lên outline chi tiết trước khi viết bản thảo: Hãy xác định trước các chương mục chính – phụ và logic giữa chúng. Điều này giúp bạn định hướng rõ ràng và không bị lạc đề trong quá trình viết.
- Tham khảo cấu trúc chuẩn quốc tế (APA, Harvard) hoặc hướng dẫn khóa luận, luận văn của trường. Mỗi trường, ngành có thể có quy định riêng về thứ tự trình bày, nên việc nắm rõ trước khi viết sẽ giúp bạn tránh sửa đi sửa lại sau này.
- Sử dụng tiêu đề phụ (Heading 2, Heading 3) rõ ràng để chia nhỏ nội dung. Việc này không chỉ giúp bài viết có mạch logic mà còn tạo trải nghiệm đọc tốt hơn cho giảng viên hoặc hội đồng phản biện.
Lỗi viết bản thảo #2: Trình bày lý thuyết rời rạc, thiếu tính liên kết
Nhiều sinh viên và nhà nghiên cứu trẻ có xu hướng sưu tầm thật nhiều tài liệu để chứng minh rằng mình “đọc nhiều”, nhưng lại chỉ dừng ở mức liệt kê lý thuyết mà không phân tích hay kết nối các nguồn. Phần cơ sở lý thuyết vì thế trở thành “bản tổng hợp copy” từ nhiều bài nghiên cứu khác, thiếu đi tư duy phản biện và sự liên kết logic.
Ví dụ: phần trình bày về “Sự hài lòng khách hàng” có thể trích dẫn 5–6 định nghĩa từ các tác giả khác nhau, nhưng không chỉ ra sự khác biệt, hoặc vì sao chọn định nghĩa nào làm cơ sở cho nghiên cứu. Kết quả là phần này không giúp hình thành một khung lý thuyết vững chắc để dẫn đến mô hình nghiên cứu sau đó.
⚠️ Hậu quả:
- Không hình thành nền tảng lý thuyết chặt chẽ, khiến mô hình nghiên cứu thiếu cơ sở khoa học.
- Bị đánh giá là thiếu tư duy phân tích, sao chép học thuật.
- Gây khó khăn khi xây dựng giả thuyết nghiên cứu và mô hình đề xuất vì thiếu sự liên kết giữa các khái niệm.
✅ Giải pháp:
- Dùng sơ đồ hoặc mô hình khái niệm để minh họa mối quan hệ giữa các biến, giúp người đọc dễ hình dung cách các khái niệm kết nối với nhau.
- Ví dụ: Vẽ sơ đồ mô tả mối quan hệ giữa “Chất lượng dịch vụ”, “Sự hài lòng”, và “Lòng trung thành khách hàng”.
- Viết lại bằng ngôn ngữ của chính mình – không chỉ thay từ, mà là diễn giải, tổng hợp và kết luận. Mỗi đoạn lý thuyết nên có một câu “chốt ý” cho thấy bạn hiểu vấn đề chứ không chỉ sao chép.
- Kết thúc phần cơ sở lý thuyết bằng mô hình đề xuất và giả thuyết nghiên cứu. Đây là cách thể hiện tư duy học thuật rõ ràng: bạn không chỉ hiểu lý thuyết, mà còn biết ứng dụng chúng vào bối cảnh nghiên cứu cụ thể.
💡 Mẹo nhỏ: Hãy xem phần “Literature Review” trong các bài quốc tế – bạn sẽ thấy họ không chỉ trích dẫn, mà luôn so sánh – tổng hợp – kết nối để dần hình thành mô hình lý thuyết của riêng mình.
Lỗi viết bản thảo #3: Diễn đạt thiếu học thuật, sử dụng ngôn ngữ cảm tính
Một lỗi phổ biến khác trong quá trình viết bản thảo của sinh viên là diễn đạt bằng ngôn ngữ cảm tính hoặc chủ quan, thay vì sử dụng văn phong học thuật và khách quan. Ví dụ, người viết thường dùng các cụm từ như:
“Tôi nghĩ rằng…”, “Theo cảm nhận của tôi…”, “Kết quả này rất tốt”, “Số liệu này khá hay”…
Những cách diễn đạt như vậy thiếu tính khách quan, khiến bài nghiên cứu giống như một bài luận cá nhân hơn là một công trình khoa học.
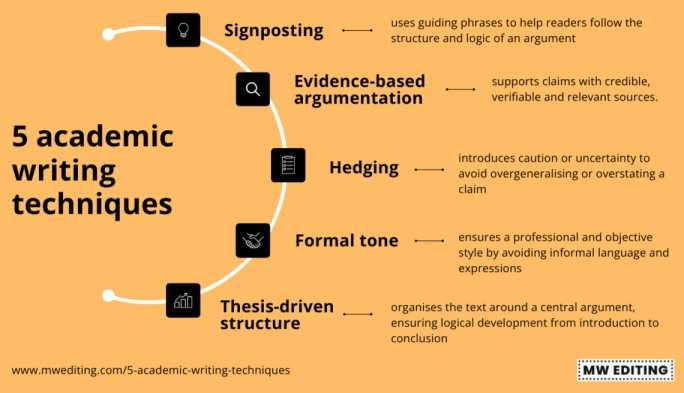
⚠️ Hậu quả:
- Làm giảm tính học thuật và độ tin cậy của bài viết.
- Người đọc hoặc hội đồng phản biện có thể đánh giá rằng tác giả thiếu kỹ năng nghiên cứu chuyên nghiệp.
- Ảnh hưởng đến khả năng công bố hoặc bảo vệ khóa luận, luận văn vì ngôn ngữ không đạt chuẩn khoa học.
✅ Giải pháp:
- Sử dụng ngôn ngữ trung tính và chuẩn học thuật:
- Thay vì viết: “Tôi nghĩ rằng kết quả này khá tốt.”
- Hãy viết: “Kết quả cho thấy xu hướng tích cực trong mối quan hệ giữa hai biến.” hoặc “Dữ liệu chỉ ra rằng sự hài lòng của khách hàng có ảnh hưởng đáng kể đến lòng trung thành.”
- Hạn chế dùng đại từ nhân xưng và tính từ cảm xúc: Trong nghiên cứu, người viết nên tránh “tôi”, “chúng tôi”, “bạn”… và các tính từ như “tuyệt vời”, “rất hay”, “khá thú vị”. Thay vào đó, hãy đưa ra bằng chứng định lượng hoặc trích dẫn học thuật để thể hiện quan điểm.
- Kiểm tra lại văn phong bằng công cụ ngữ pháp học thuật.
- Gợi ý công cụ: Grammarly Academic, Quillbot Academic, hoặc Writefull giúp phát hiện lỗi chủ quan và gợi ý cách diễn đạt học thuật hơn.
- Ngoài ra, có thể tham khảo các bài nghiên cứu quốc tế (Scopus, ScienceDirect) để học cách hành văn, cách chuyển đoạn, và cách trình bày kết quả mang tính học thuật cao.
💡 Mẹo nhỏ: Trước khi nộp bài, hãy đọc lại toàn bộ bản thảo và thử loại bỏ tất cả các từ cảm xúc – nếu ý nghĩa câu vẫn đủ mạnh và logic, bạn đã đạt chuẩn học thuật.
Lỗi viết bản thảo #4: Trích dẫn và tài liệu tham khảo không đúng chuẩn
Một lỗi học thuật nghiêm trọng mà nhiều sinh viên và nhà nghiên cứu thường mắc phải khi viết bản thảo là trích dẫn sai hoặc không trích dẫn đầy đủ nguồn tham khảo. Ví dụ phổ biến:
- Dẫn ý nhưng không ghi nguồn hoặc chỉ ghi “theo một số nghiên cứu”.
- Trích dẫn trong nội dung không khớp với danh mục tài liệu tham khảo ở cuối bài.
- Dùng định dạng lộn xộn giữa nhiều chuẩn (vừa APA, vừa Harvard).
- Sao chép đoạn văn từ tài liệu khác mà không ghi rõ trích dẫn — vô tình vi phạm đạo văn (plagiarism).
Nhiều sinh viên nghĩ rằng chỉ cần “ghi tên tác giả ở phần cuối” là đủ, nhưng trên thực tế, mỗi trích dẫn trong nội dung phải có đối chiếu rõ ràng với tài liệu tham khảo tương ứng, theo đúng chuẩn học thuật của bài nghiên cứu.

⚠️ Hậu quả:
- Làm giảm điểm đáng kể ở phần trình bày hoặc tính trung thực học thuật.
- Có thể bị hội đồng đánh giá nghi ngờ đạo văn, ảnh hưởng nghiêm trọng đến uy tín cá nhân.
- Trong công bố quốc tế, vi phạm trích dẫn có thể dẫn đến việc bài bị từ chối hoặc rút lại sau khi đăng.
✅ Giải pháp:
- Sử dụng một chuẩn trích dẫn thống nhất xuyên suốt bài viết.
- Thông thường, các trường đại học và tạp chí khuyến khích dùng các chuẩn như:
- APA (American Psychological Association) – phổ biến trong khoa học xã hội, giáo dục, tâm lý học.
- Harvard – dùng nhiều trong kinh tế, quản trị.
- Chicago hoặc IEEE – thường gặp trong kỹ thuật, công nghệ.
- Lưu ý: Dùng duy nhất một chuẩn cho toàn bộ bài để đảm bảo tính nhất quán.
- Thông thường, các trường đại học và tạp chí khuyến khích dùng các chuẩn như:
- Dùng công cụ quản lý tài liệu chuyên dụng: giúp bạn tự động tạo trích dẫn và danh mục tài liệu tham khảo đúng chuẩn, hạn chế tối đa lỗi định dạng.
- Mendeley: Miễn phí, dễ dùng, tích hợp Word và tự động định dạng trích dẫn.
- Zotero: Hỗ trợ lưu trữ và trích dẫn trực tiếp từ trình duyệt.
- EndNote: Mạnh mẽ, thường được các học viên cao học hoặc nhà nghiên cứu chuyên nghiệp sử dụng.
- Kiểm tra kỹ phần tài liệu tham khảo trước khi nộp.
- Đảm bảo mọi trích dẫn trong nội dung đều có mặt trong danh mục tài liệu tham khảo.
- Sắp xếp danh mục theo thứ tự alphabet (A–Z) đúng quy định.
- Với nguồn tiếng Việt, nên ghi rõ tác giả – năm – tên bài – nhà xuất bản hoặc nguồn trực tuyến.
💡 Mẹo nhỏ: Trước khi nộp bài, hãy chạy kiểm tra plagiarism (Turnitin, iThenticate) để đảm bảo mức độ tương đồng thấp (<20%) và toàn bộ nguồn trích dẫn đã được ghi nhận đúng cách.
Lỗi viết bản thảo #5: Thiếu liên kết giữa kết quả – thảo luận – kết luận
Một lỗi rất thường gặp trong khóa luận, luận văn hoặc bài nghiên cứu là phần kết quả chỉ dừng lại ở việc liệt kê số liệu, bảng biểu, mà thiếu phần diễn giải ý nghĩa khoa học. Người viết thường tập trung trình bày chi tiết các con số — ví dụ như “Giá trị Sig = 0.032” hay “R² = 0.57” — nhưng không giải thích chúng nói lên điều gì, cũng không so sánh với giả thuyết nghiên cứu hoặc các nghiên cứu trước đó. Kết quả là bài viết dù có đủ dữ liệu phân tích, nhưng không tạo được giá trị học thuật hay kết nối logic giữa lý thuyết – mô hình – kết luận.

⚠️ Hậu quả:
- Phần kết quả trở nên khô khan, giống như báo cáo thống kê hơn là một bài nghiên cứu.
- Thiếu tính thuyết phục, vì người đọc không hiểu ý nghĩa của con số trong bối cảnh nghiên cứu.
- Làm mất cơ hội thể hiện năng lực phân tích và tư duy khoa học – yếu tố mà hội đồng phản biện đánh giá rất cao.
✅ Giải pháp:
Để phần thảo luận và kết luận trở nên có chiều sâu, hãy luôn đảm bảo trả lời đủ 3 câu hỏi cốt lõi sau:
- Kết quả này có ý nghĩa gì? → Giải thích xem kết quả cho thấy điều gì về mối quan hệ giữa các biến, có phù hợp với kỳ vọng của bạn không.
- So với các nghiên cứu trước ra sao? → So sánh kết quả với các công trình tương tự. Nếu khác biệt, cần lý giải vì sao (khác mẫu, khác bối cảnh, khác phương pháp…).
- Tác động thực tiễn là gì? → Liên hệ kết quả với ứng dụng trong thực tế: doanh nghiệp, chính sách, hoặc hành vi xã hội.
Ngoài ra, khi viết phần kết luận, cần:
- Tóm tắt ngắn gọn các phát hiện chính, tránh lặp lại toàn bộ số liệu.
- Kết nối chặt chẽ với mục tiêu và giả thuyết nghiên cứu.
- Đề xuất hướng nghiên cứu tiếp theo để mở rộng giá trị học thuật của đề tài.
💡 Mẹo nhỏ: Một bài nghiên cứu hay không phải bài có nhiều số liệu nhất, mà là bài biết kể câu chuyện khoa học rõ ràng thông qua việc phân tích – đối chiếu – lý giải – rút ra kết luận từ những con số đó.
Kết luận
Viết bản thảo nghiên cứu không chỉ là bước ghi chép lại kết quả, mà là một quá trình khoa học đòi hỏi kỹ năng, sự tỉ mỉ và tư duy học thuật cao. Mỗi phần – từ mở đầu, cơ sở lý thuyết, phương pháp, đến kết quả và kết luận – đều cần được xây dựng một cách logic, chuẩn cấu trúc và có giá trị phân tích.
Top 5 lỗi phổ biến khi viết bản thảo mà sinh viên và nhà nghiên cứu thường mắc phải – bao gồm:
1️⃣ Viết thiếu cấu trúc logic.
2️⃣ Sao chép lý thuyết mà không tổng hợp.
3️⃣ Diễn đạt cảm tính, thiếu học thuật.
4️⃣ Trích dẫn sai quy chuẩn.
5️⃣ Không thảo luận, chỉ liệt kê số liệu.
…chính là những “chướng ngại vật” lớn nhất cản trở bạn đạt được một bản thảo nghiên cứu chất lượng.
Tránh được 5 lỗi viết bản thảo trên không chỉ giúp bài viết của bạn đạt chuẩn học thuật và dễ được chấp nhận, mà còn thể hiện bạn là một người có tư duy nghiên cứu chuyên nghiệp, hiểu rõ quy trình khoa học. Đây chính là bước khởi đầu vững chắc cho một đề tài tốt nghiệp xuất sắc hoặc bài báo khoa học được phản biện cao.
👉 Truy cập ngay “Bộ tài liệu hướng dẫn nghiên cứu khoa học” miễn phí tại đây: https://xulysolieu.info/bo-tai-lieu-huong-dan-guideline-ho-tro-nghien-cuu/
👉 Hoặc liên hệ trực tiếp với Xử Lý Số Liệu để được:
- Tư vấn về cấu trúc bản thảo, trích dẫn và cách trình bày học thuật,
- Đánh giá miễn phí bản thảo trước khi nộp cho GVHD hoặc bảo vệ.
- Hỗ trợ viết nội dung nghiên cứu, xử lý phân tích số liệu, hiệu chỉnh toàn văn,…
Xử Lý Số Liệu – Đồng hành cùng bạn trên hành trình khoa học chuyên nghiệp!














