Varimax Rotation là gì? Phép quay vuông góc Varimax & phép quay không vuông góc Promax
Trong phân tích nhân tố EFA, sau bước trích nhân tố, một câu hỏi quan trọng luôn được đặt ra là: làm thế nào để các nhân tố trở nên dễ hiểu và có ý nghĩa hơn? Câu trả lời nằm ở phép quay nhân tố (factor rotation), trong đó varimax rotation là kỹ thuật được sử dụng phổ biến nhất.
Bài viết này sẽ giúp bạn hiểu rõ bản chất của varimax rotation, cách nó hoạt động trong phân tích nhân tố EFA, sự khác biệt giữa varimax vs promax, và cách lựa chọn phép quay phù hợp trong thực hành phân tích dữ liệu.
1. Phép quay nhân tố (Factor Rotation) là gì?
Trong phân tích nhân tố EFA, mục tiêu cốt lõi là rút gọn một tập lớn biến quan sát thành một số ít nhân tố tiềm ẩn có ý nghĩa. Tuy nhiên, nếu chỉ dừng lại ở bước trích nhân tố, các biến quan sát thường có xu hướng tải lên nhiều nhân tố cùng lúc.
Hiện tượng này khiến việc diễn giải trở nên khó khăn vì:
- Một biến có factor loading trung bình ở nhiều nhân tố
- Không xác định rõ biến đó đại diện cho nhân tố nào
- Cấu trúc nhân tố thiếu rõ ràng
Phép quay nhân tố (factor rotation) ra đời nhằm giải quyết vấn đề này. Bản chất của phép quay là xoay các trục nhân tố trong không gian đa chiều để đạt được cấu trúc nhân tố đơn giản, nơi mỗi biến quan sát:
- Tải mạnh (factor loading cao) lên một nhân tố
- Tải rất yếu lên các nhân tố còn lại
Đây chính là nền tảng lý thuyết cho varimax rotation.
2. Varimax Rotation là gì?
Varimax rotation là một phép quay vuông góc (orthogonal rotation), nghĩa là sau khi quay, các trục nhân tố vẫn giữ nguyên góc 90 độ với nhau. Điều này đồng nghĩa với một giả định quan trọng:
Các nhân tố không có tương quan với nhau.
Mục tiêu của varimax rotation là tối đa hóa phương sai của bình phương factor loading trong mỗi nhân tố. Nói đơn giản hơn:
- Hệ số tải cao → càng cao hơn
- Hệ số tải thấp → càng thấp hơn
Kết quả là mỗi biến quan sát sẽ “thuộc” rõ ràng về một nhân tố cụ thể, giúp việc đặt tên và diễn giải nhân tố trở nên trực quan.
Trong thực hành phân tích nhân tố EFA, varimax rotation thường được xem là lựa chọn mặc định, đặc biệt với người mới học phân tích dữ liệu.
3. Ví dụ trực quan về Varimax Rotation trong EFA
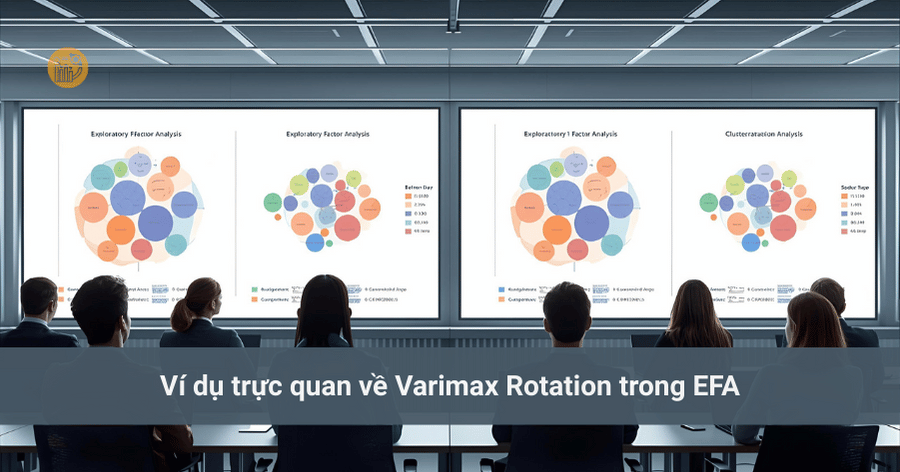
Giả sử bạn có 15 biến quan sát đo lường 3 khái niệm khác nhau. Nếu chưa áp dụng varimax rotation, mỗi biến có thể tải lên cả 3 nhân tố với mức độ tương đối giống nhau.
Sau khi áp dụng varimax rotation:
- Nhóm biến DT1–DT5 có factor loading rất cao ở nhân tố 1
- Nhóm biến LD1–LD4 tải mạnh ở nhân tố 2
- Nhóm biến TL1–TL4 tải mạnh ở nhân tố 3
Khi đó, từ 15 biến ban đầu, bạn chỉ cần làm việc với 3 nhân tố tiềm ẩn. Đây chính là giá trị cốt lõi mà varimax rotation mang lại trong phân tích nhân tố EFA.
4. Các nhóm phép quay nhân tố trong EFA
Trong phân tích nhân tố EFA, các phép quay được chia thành hai nhóm chính:
4.1. Phép quay vuông góc (Orthogonal Rotation)
- Varimax
- Equimax
- Quartimax
Trong nhóm này, varimax rotation là phổ biến nhất do dễ diễn giải và phù hợp với nhiều mục tiêu nghiên cứu.
4.2. Phép quay không vuông góc (Oblique Rotation)
- Promax
- Oblimin
- Orthoblique
Các phép quay này cho phép các nhân tố có tương quan với nhau, phù hợp với nhiều mô hình lý thuyết xã hội – hành vi.
5. Varimax vs Promax: Nên chọn phép quay nào?
So sánh varimax vs promax là câu hỏi rất thường gặp khi làm phân tích nhân tố EFA.
Varimax Rotation
- Phép quay vuông góc
- Giả định các nhân tố độc lập
- Dễ diễn giải
- Phù hợp khi phân tích hồi quy, tương quan
Promax Rotation
- Phép quay không vuông góc
- Cho phép các nhân tố tương quan
- Phù hợp khi có biến trung gian
- Thường dùng trước phân tích SEM
Nhiều nghiên cứu cho thấy sự khác biệt giữa varimax vs promax không quá lớn về mặt kết quả thống kê. Việc lựa chọn chủ yếu phụ thuộc vào mô hình lý thuyết và bước phân tích tiếp theo.
6. Varimax Rotation và phương pháp trích nhân tố
Varimax rotation thường được sử dụng cùng với:
- Principal Component Analysis (PCA): khi mục tiêu là giảm chiều dữ liệu
- Phân tích khám phá ban đầu, tập trung vào phương sai trích
Ngược lại, Promax thường kết hợp với Principal Axis Factoring để khám phá nhân tố tiềm ẩn đúng nghĩa.
7. Đọc Factor Loading sau Varimax Rotation
Sau khi áp dụng varimax rotation, bạn cần chú ý:
- Factor loading ≥ 0.5: biến đại diện tốt cho nhân tố
- Không nên có tải chéo cao ở nhiều nhân tố
- Biến vi phạm cấu trúc đơn giản nên bị loại
Đây là bước then chốt để đảm bảo chất lượng của phân tích nhân tố EFA.
8. Kết luận
Varimax rotation là công cụ nền tảng trong phân tích nhân tố EFA, giúp đơn giản hóa cấu trúc nhân tố, tăng khả năng diễn giải và hỗ trợ các phân tích tiếp theo như hồi quy hay tương quan.
Hiểu đúng bản chất của varimax rotation, nắm rõ sự khác biệt giữa varimax vs promax, và đọc chính xác factor loading sẽ giúp bạn làm chủ hoàn toàn kỹ thuật EFA trong nghiên cứu và thực hành xử lý số liệu.
Nếu bạn cần hỗ trợ học và thực hành phân tích nhân tố EFA, hãy tham khảo các tài liệu chuyên sâu tại xulysolieu.info – Xử lý số liệu hoặc liên hệ 0878968468 để được tư vấn trực tiếp.
Cách tra bảng độ tin cậy Cronbach’s Alpha trong SPSS
Trong các nghiên cứu định lượng, đặc biệt là nghiên cứu kinh tế – xã hội, việc cách tra bảng độ tin cậy là bước bắt buộc trước khi thực hiện EFA, CFA hay hồi quy. Trong đó, Cronbach’s Alpha là chỉ số phổ biến nhất dùng để đánh giá độ tin cậy thang đo. Bài viết này tập trung hướng dẫn cách tra bảng độ tin cậy Cronbach’s Alpha trong SPSS theo hướng dễ hiểu, đi thẳng vào bản chất và cách đọc kết quả.
1. Hiểu đúng thang đo khi tra bảng độ tin cậy
Trước khi học cách tra bảng độ tin cậy, cần hiểu đúng khái niệm “thang đo”. Trong phân tích dữ liệu, thang đo không phải là thang Likert 1–5 hay 1–7, mà là tập hợp các biến quan sát cùng đo lường một khái niệm trừu tượng như: sự hài lòng, chất lượng dịch vụ, động lực làm việc, lòng trung thành.
Một thang đo tốt cần đảm bảo:
- Các biến quan sát cùng phản ánh một nhân tố chung
- Không trùng lặp nội dung
- Có mối liên hệ chặt chẽ với nhau
Do đó, cách tra bảng độ tin cậy Cronbach Alpha thực chất là kiểm tra mức độ nhất quán nội bộ của các biến quan sát trong cùng một thang đo.
2. Cronbach Alpha và ý nghĩa trong độ tin cậy thang đo
Cronbach Alpha là chỉ số đo lường mức độ nhất quán nội bộ (internal consistency). Khi các biến quan sát biến động cùng chiều và có mối liên hệ chặt chẽ, hệ số này sẽ cao.
Trong reliability analysis, Cronbach Alpha giúp trả lời hai câu hỏi quan trọng:
- Thang đo này có đủ độ tin cậy thang đo để sử dụng hay không?
- Biến quan sát nào là biến tốt, biến nào cần loại biến rác?
Vì vậy, nắm vững cách tra bảng độ tin cậy Cronbach’s Alpha là kỹ năng nền tảng khi làm phân tích dữ liệu với SPSS.
3. Tiêu chuẩn khi tra bảng độ tin cậy Cronbach’s Alpha
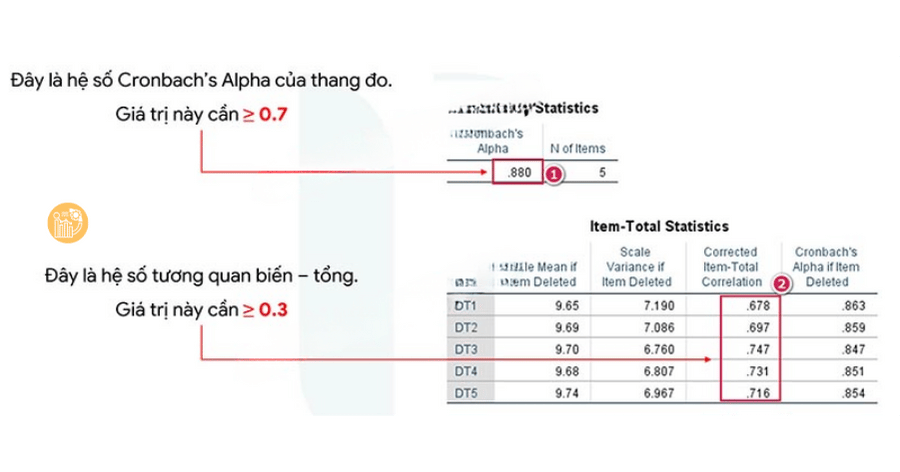
Khi thực hiện spss reliability, việc cách tra bảng độ tin cậy cần dựa trên hai tiêu chuẩn chính:
3.1. Hệ số Cronbach’s Alpha của thang đo
- Cronbach’s Alpha ≥ 0.7: thang đo tốt
- 0.6 ≤ Cronbach’s Alpha < 0.7: chấp nhận với nghiên cứu khám phá
- Cronbach’s Alpha < 0.6: thang đo chưa đạt
Khi tra bảng Reliability Statistics trong SPSS, đây là chỉ số đầu tiên cần xem trong cách tra bảng độ tin cậy.
3.2. Hệ số tương quan biến tổng
Hệ số tương quan biến tổng (Corrected Item – Total Correlation) phản ánh mức độ đóng góp của từng biến quan sát vào thang đo chung.
- ≥ 0.3: biến đạt yêu cầu
- < 0.3: biến yếu, nên xem xét loại
Trong cách tra bảng độ tin cậy, đây là tiêu chí quan trọng để loại biến rác.
4. Ý nghĩa cột Cronbach’s Alpha if Item Deleted
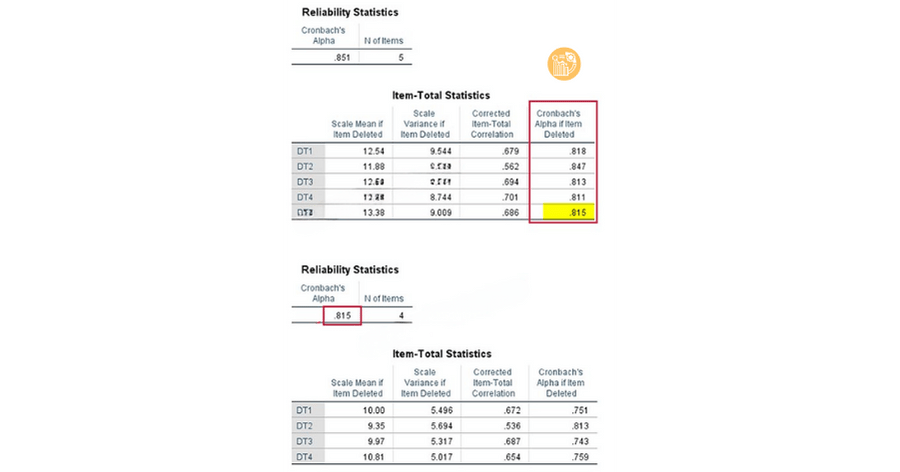
Nhiều người mới học thường nhầm lẫn rằng Cronbach’s Alpha if Item Deleted là “độ tin cậy của từng biến”. Đây là cách hiểu sai.
Thực chất, cột này cho biết:
- Nếu loại biến đó, Cronbach Alpha của thang đo sẽ bằng bao nhiêu
- Biến nào đang làm giảm độ tin cậy chung
Trong cách tra bảng độ tin cậy:
- Nếu Alpha if Item Deleted > Alpha chung và thang đo chưa đạt → nên loại
- Nếu Alpha chung đã đạt và tương quan biến tổng ≥ 0.3 → không bắt buộc loại
5. Quy trình cách tra bảng độ tin cậy trong SPSS
Các bước thực hiện reliability analysis trong SPSS:

- Analyze → Scale → Reliability Analysis
- Đưa các biến của một thang đo vào Items
- Chọn Statistics → tick Item, Scale, Scale if item deleted
- OK để xuất kết quả
Lưu ý quan trọng trong cách tra bảng độ tin cậy: không đưa nhiều thang đo vào chạy chung một lần.
6. Các trường hợp thường gặp khi tra bảng độ tin cậy
Trường hợp 1: Thang đo đạt, biến đạt
Cronbach Alpha ≥ 0.6 và tất cả hệ số tương quan biến tổng ≥ 0.3. Thang đo đạt, giữ nguyên.

Trường hợp 2: Thang đo đạt, có biến rác
Cronbach Alpha đạt nhưng có biến có tương quan biến tổng < 0.3. Tiến hành loại biến rác và chạy lại.
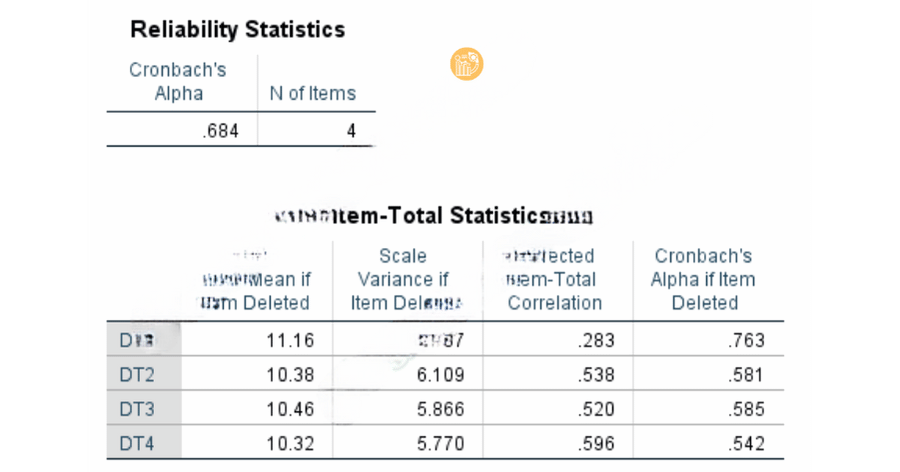
Trường hợp 3: Alpha if Item Deleted lớn hơn Alpha chung
Nếu thang đo đã đạt và biến vẫn có hệ số tương quan biến tổng đạt, không bắt buộc loại.
Trường hợp 4: Thang đo không đạt
Cronbach Alpha < 0.6. Kiểm tra Alpha if Item Deleted, loại biến giúp Alpha vượt 0.6. Nếu không cải thiện, loại cả thang đo.
7. Những lưu ý quan trọng khi áp dụng cách tra bảng độ tin cậy
- Không kết luận vội khi Alpha < 0.6
- Luôn ưu tiên hệ số tương quan biến tổng
- Không chạy chung nhiều thang đo
- Cronbach Alpha không dùng cho từng biến riêng lẻ
Việc nắm chắc cách tra bảng độ tin cậy giúp bạn tránh sai sót phổ biến và đảm bảo chất lượng dữ liệu trước các phân tích tiếp theo.
8. Hỗ trợ xử lý số liệu SPSS
Nếu bạn gặp khó khăn khi cách tra bảng độ tin cậy, phân tích cronbach alpha, spss reliability hoặc cần hỗ trợ Xử lý số liệu, bạn có thể tham khảo tại:
xulysolieu.info
Hotline/Zalo: 0878968468
Việc hiểu đúng và áp dụng chuẩn cách tra bảng độ tin cậy không chỉ giúp nghiên cứu đạt yêu cầu học thuật mà còn nâng cao chất lượng phân tích dữ liệu trong thực tiễn.
Cách tính phương sai trong SPSS bằng ANOVA
Trong phân tích dữ liệu thống kê, cách tính phương sai trong SPSS là một nội dung nền tảng mà bất kỳ người học SPSS nào cũng cần nắm vững. Phương sai (variance) giúp đo lường mức độ phân tán của dữ liệu, và trong nhiều nghiên cứu khoa học, phương sai được sử dụng thông qua kiểm định ANOVA.
Bài viết này của xulysolieu.info – Xử lý số liệu sẽ hướng dẫn chi tiết cách tính phương sai trong SPSS bằng phương pháp ANOVA, từ lý thuyết cơ bản đến thực hành và cách đọc kết quả.
1. Phương sai (Variance) và vai trò trong phân tích dữ liệu
Phương sai (variance) là thước đo thể hiện mức độ các giá trị dữ liệu phân tán quanh giá trị trung bình. Trong thống kê, phương sai variance càng lớn thì dữ liệu càng phân tán mạnh.
Khi so sánh trung bình của nhiều nhóm dữ liệu, thay vì chỉ nhìn vào trung bình, người nghiên cứu cần xét đến phương sai để đánh giá sự khác biệt có ý nghĩa hay không. Đó là lý do cách tính phương sai trong SPSS thường được thực hiện thông qua phân tích phương sai ANOVA.
2. Phân tích phương sai (ANOVA) là gì?
Phân tích phương sai (Analysis of Variance – ANOVA) là phương pháp thống kê dùng để so sánh trung bình của từ ba nhóm trở lên. Bản chất của ANOVA không chỉ so sánh trung bình mà còn dựa trên cách tính phương sai trong SPSS giữa các nhóm và trong từng nhóm.
ANOVA phân tách tổng phương sai thành hai thành phần chính:
- Between Groups: phương sai giữa các nhóm.
- Within Groups: phương sai trong từng nhóm.
Việc so sánh Between Groups và Within Groups chính là cốt lõi của kiểm định ANOVA.
3. Các giả định khi áp dụng ANOVA trong SPSS
Trước khi áp dụng cách tính phương sai trong SPSS bằng ANOVA, dữ liệu cần thỏa mãn một số giả định:
- Các nhóm quan sát độc lập.
- Dữ liệu biến phụ thuộc có phân phối chuẩn (hoặc cỡ mẫu đủ lớn).
- Phương sai của các nhóm tương đối đồng nhất.
Nếu các giả định này bị vi phạm, kết quả phân tích phương sai có thể không còn đáng tin cậy.
4. Các loại ANOVA thường dùng trong SPSS
Trong thực tế nghiên cứu, anova trong SPSS thường được sử dụng dưới hai dạng phổ biến:
4.1. ANOVA một yếu tố (One-way ANOVA)
ANOVA một yếu tố dùng để phân tích ảnh hưởng của một biến định tính (yếu tố nguyên nhân) lên một biến định lượng (kết quả). Đây là dạng phổ biến nhất khi học cách tính phương sai trong SPSS.
4.2. ANOVA hai yếu tố (Two-way ANOVA)
ANOVA hai yếu tố cho phép kiểm tra đồng thời ảnh hưởng của hai biến định tính lên một biến định lượng. Cách tiếp cận này giúp mô hình nghiên cứu có giá trị giải thích cao hơn.
5. Trình tự thực hiện cách tính phương sai trong SPSS bằng ANOVA
Để thực hiện cách tính phương sai trong SPSS bằng ANOVA một yếu tố, bạn làm theo các bước sau:
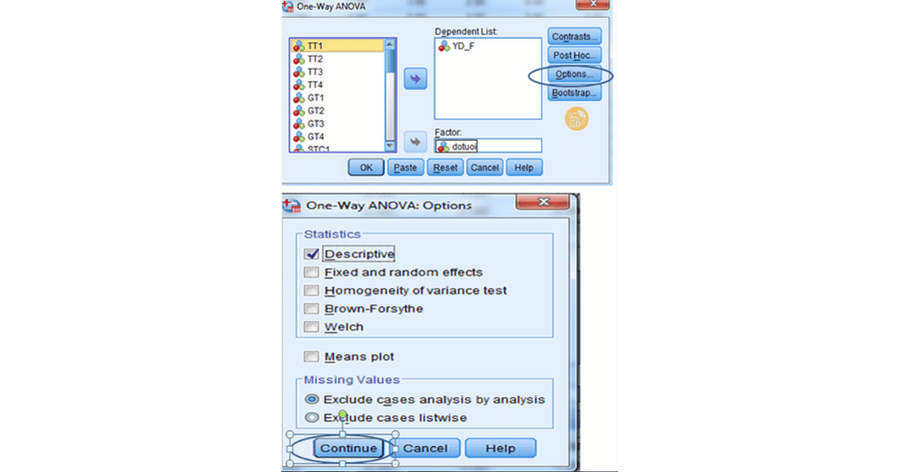
Bước 1: Mở hộp thoại ANOVA
Vào menu:
Analyze → Compare Means → One-Way ANOVA

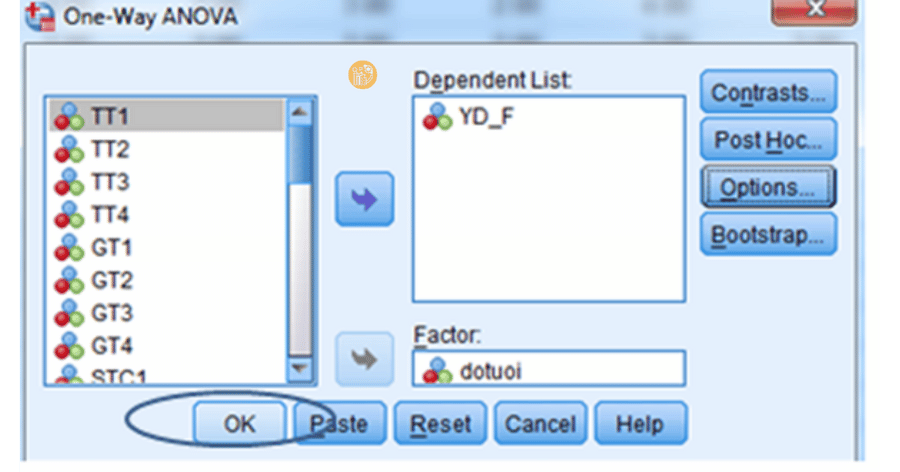
Bước 2: Chọn biến phân tích
Đưa biến phụ thuộc (định lượng) vào ô Dependent List. Đưa biến phân nhóm (định tính) vào ô Factor.

Bước 3: Chọn Post Hoc
Chọn Tukey để so sánh cặp khi có từ ba nhóm trở lên. Bước này giúp làm rõ sự khác biệt giữa các nhóm sau khi đã áp dụng cách tính phương sai trong SPSS.
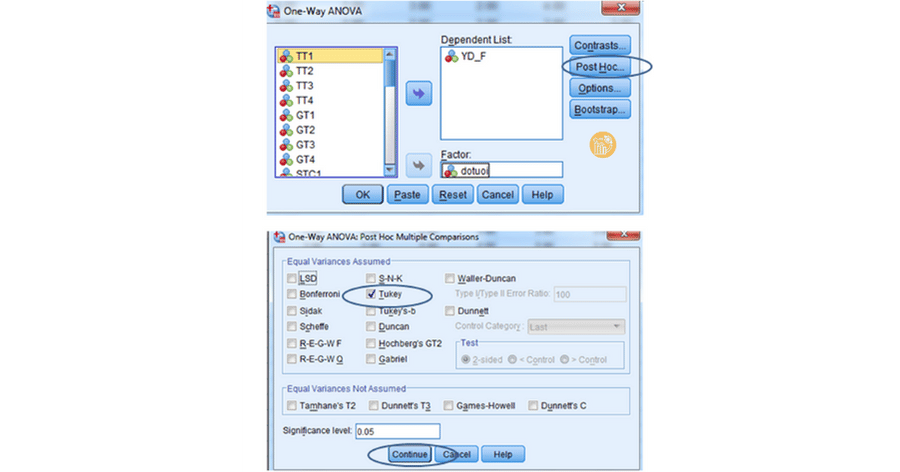
Bước 4: Chọn Options
Tích chọn Descriptive để hiển thị thống kê mô tả. Sau đó nhấn OK để chạy phân tích.
6. Cách đọc kết quả cách tính phương sai trong SPSS
6.1. Bảng Descriptives
Bảng Descriptives cung cấp:
- Giá trị trung bình.
- Độ lệch chuẩn.
- Số quan sát của từng nhóm.
Đây là bước đầu giúp hiểu dữ liệu trước khi đi sâu vào kiểm định ANOVA.
6.2. Bảng ANOVA
Bảng ANOVA là kết quả trung tâm của cách tính phương sai trong SPSS. Trong bảng này, bạn cần chú ý:
- Between Groups: phương sai giữa các nhóm.
- Within Groups: phương sai trong nhóm.
- Giá trị Sig. (p-value).
Nếu Sig. < 0.05, kết luận có sự khác biệt có ý nghĩa thống kê giữa các nhóm.
6.3. Bảng Multiple Comparisons
Bảng này cho biết nhóm nào khác nhóm nào. Dựa vào cột Sig., bạn xác định cặp nhóm có sự khác biệt có ý nghĩa thống kê.
7. Ý nghĩa của Between Groups và Within Groups
Trong cách tính phương sai trong SPSS, Between Groups phản ánh mức độ khác biệt giữa trung bình các nhóm. Within Groups phản ánh mức độ phân tán dữ liệu trong từng nhóm.
Khi Between Groups lớn hơn nhiều so với Within Groups, giá trị F sẽ lớn và khả năng bác bỏ giả thuyết H0 càng cao.
8. Kết luận
Cách tính phương sai trong SPSS bằng ANOVA là kỹ năng cốt lõi trong phân tích dữ liệu định lượng. Thông qua phân tích phương sai, người nghiên cứu có thể đánh giá sự khác biệt giữa nhiều nhóm một cách khoa học và có cơ sở thống kê.
Nếu bạn nắm vững cách tính phương sai trong SPSS, việc đọc kết quả kiểm định, giải thích nghiên cứu và viết luận văn sẽ trở nên dễ dàng hơn rất nhiều.
Để tìm hiểu thêm các hướng dẫn chuyên sâu về SPSS, ANOVA và phân tích dữ liệu, bạn có thể tham khảo tại xulysolieu.info – Xử lý số liệu.
Cách khai báo biến SPSS & Nhập liệu cho người mới
Trong quá trình học và làm phân tích dữ liệu, cách khai báo biến SPSS là bước đầu tiên và quan trọng nhất. Nếu khai báo biến sai, toàn bộ các bước phân tích phía sau như thống kê mô tả, hồi quy hay ANOVA đều có thể cho kết quả sai lệch. Bài viết này từ xulysolieu.info – Xử lý số liệu sẽ hướng dẫn cách khai báo biến, nhập liệu trong SPSS một cách bài bản, dễ hiểu cho người mới bắt đầu.
Vì sao cần hiểu rõ cách khai báo biến SPSS?
Khi làm việc với SPSS, phần mềm không “hiểu” dữ liệu theo nghĩa tự nhiên mà hiểu thông qua cách bạn khai báo biến. Do đó, nắm vững cách khai báo biến SPSS giúp:
- Xác định đúng kiểu dữ liệu của biến
- Áp dụng đúng phép phân tích thống kê
- Tránh lỗi khi chạy kiểm định
- Tăng độ chính xác và độ tin cậy của kết quả
Vì vậy, học cách khai báo biến là nền tảng bắt buộc cho mọi nghiên cứu định lượng.
Giao diện Variable View và Data View trong SPSS
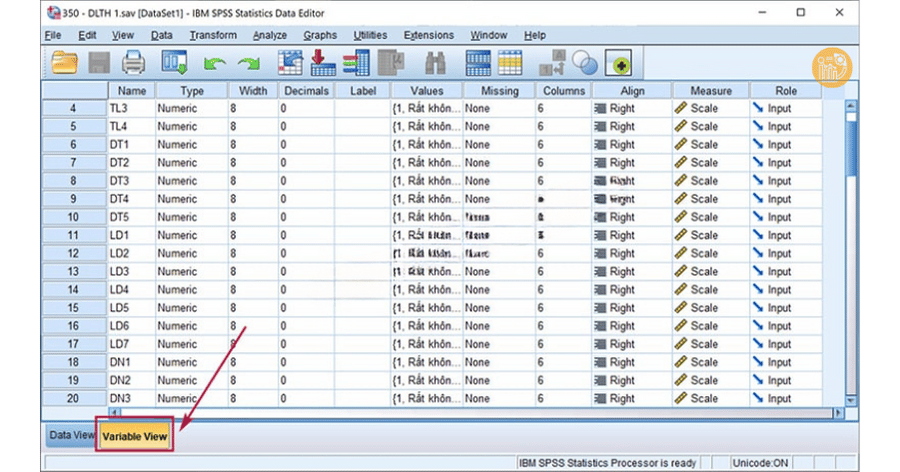
Để thực hiện cách khai báo biến, bạn cần làm quen với hai giao diện chính:
- Variable View SPSS: nơi khai báo đặc tính của biến
- Data View SPSS: nơi nhập dữ liệu quan sát
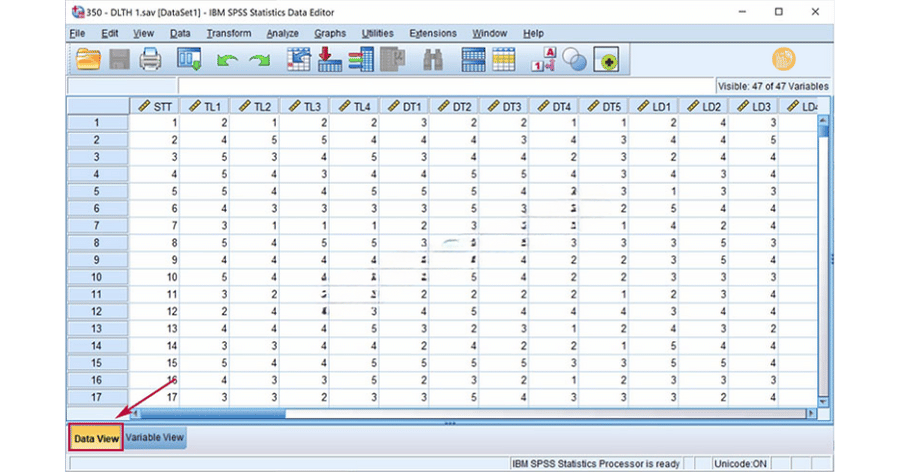
Có thể hình dung Variable View SPSS là phần tạo “khuôn”, còn Data View SPSS là phần “đổ dữ liệu” vào khuôn đó. Hai phần này luôn song hành trong quá trình nhập liệu trong SPSS.
Cách khai báo biến SPSS trong Variable View
Để bắt đầu cách khai báo biến, bạn mở SPSS và chuyển sang tab Variable View ở góc dưới màn hình. Mỗi hàng tương ứng với một biến, mỗi cột thể hiện một thuộc tính của biến.
Name – Tên biến
Trong cách khai báo, Name là tên kỹ thuật của biến. Tên biến cần tuân thủ các nguyên tắc:
- Không dùng dấu tiếng Việt
- Không có khoảng trắng
- Không bắt đầu bằng số
- Dùng dấu gạch dưới (_) để nối từ
Ví dụ hợp lệ: GioiTinh, DoTuoi, HocVan, ThuNhap_Thang Ví dụ không hợp lệ: Giới tính, Độ tuổi, 1NgheNghiep
Type – Kiểu dữ liệu
Type biến SPSS cho biết dữ liệu của biến thuộc dạng nào. Trong thực tế, hai loại phổ biến nhất là:
- Numeric: dữ liệu dạng số
- String: dữ liệu dạng chữ
Khi thực hiện cách khai báo biến SPSS, bạn nên ưu tiên Numeric để thuận tiện cho phân tích, trừ trường hợp bắt buộc phải dùng String.
Width và Decimals
Width là số ký tự tối đa, Decimals là số chữ số thập phân. Trong cách khai báo biến, bạn nên:
- Để Decimals = 0 nếu dữ liệu là số nguyên
- Tăng Decimals nếu dữ liệu có phần thập phân
- Không để Width quá lớn gây nặng file
Label – Nhãn biến
Label và Value là phần rất quan trọng trong cách khai báo biến SPSS. Label dùng để mô tả đầy đủ ý nghĩa của biến và có thể viết tiếng Việt có dấu.
Ví dụ: Name: GioiTinh Label: Giới tính của người trả lời
Values – Gán giá trị cho biến
Label và Value giúp SPSS hiểu ý nghĩa của các con số mã hóa. Ví dụ:
- 1 = Nam
- 2 = Nữ
Đây là bước không thể thiếu khi thực hiện cách khai báo biến cho câu hỏi định tính.
Missing – Giá trị khuyết
Trong cách khai báo biến SPSS, Missing dùng để khai báo dữ liệu thiếu. Ví dụ, bạn có thể quy ước:
- 99: không phù hợp
- 88: không trả lời
Việc khai báo missing giúp SPSS xử lý dữ liệu chính xác hơn khi phân tích.
Measure – Thang đo
Measure cho biết loại thang đo của biến. Đây là yếu tố cốt lõi trong khai báo biến.
- Nominal: định danh
- Ordinal: thứ bậc
- Scale: khoảng / tỷ lệ
Việc chọn đúng scale nominal ordinal quyết định SPSS cho phép bạn chạy những phân tích nào.
Nhập liệu trong SPSS bằng Data View
Sau khi hoàn thành cách khai báo biến, bạn chuyển sang Data View SPSS để nhập dữ liệu.
- Mỗi cột: một biến
- Mỗi hàng: một đối tượng quan sát
Nhập liệu trong SPSS cần tuân thủ đúng mã hóa đã khai báo để tránh lỗi khi phân tích.
Thực hành khai báo biến SPSS theo từng loại câu hỏi
Câu hỏi định tính một trả lời
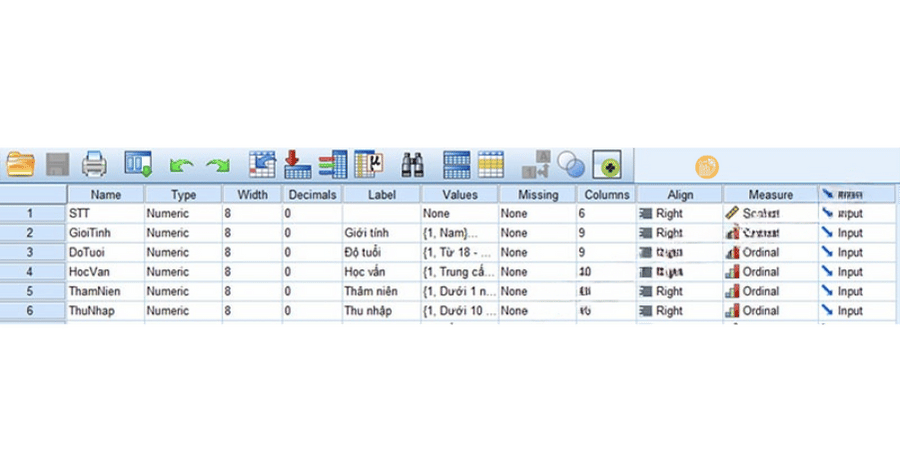
Với câu hỏi như giới tính, độ tuổi, học vấn, mỗi câu hỏi tương ứng một biến. Đây là dạng phổ biến nhất khi áp dụng cách khai báo biến.
- Type: Numeric
- Measure: Nominal hoặc Ordinal
- Values: mã hóa từng đáp án
Câu hỏi định lượng một trả lời
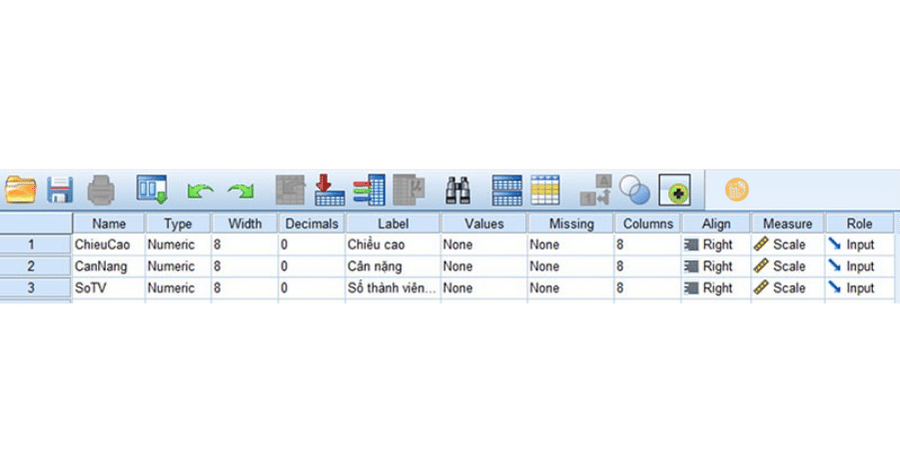
Câu hỏi về chiều cao, cân nặng, điểm số, Likert scale là câu hỏi định lượng. Trong cách khai báo biến cho dạng này:
- Type: Numeric
- Measure: Scale
- Không cần gán Values
Câu hỏi định tính nhiều trả lời
Câu hỏi nhiều trả lời cần tạo nhiều biến con hoặc dùng hệ nhị phân. Đây là phần nâng cao trong cách khai báo biến và thường gây nhầm lẫn cho người mới.
SPSS cho phép tổng hợp các biến này thông qua Multiple Response Sets để phân tích.
Những lỗi thường gặp khi khai báo biến SPSS
- Đặt sai Measure
- Không gán Value cho biến định tính
- Nhập dữ liệu không đúng mã hóa
- Không khai báo missing value
Những lỗi này đều xuất phát từ việc chưa nắm vững cách khai báo biến.
Tổng kết
Qua bài viết này, bạn đã nắm được cách khai báo biến một cách hệ thống, từ Variable View SPSS, Data View SPSS, type biến SPSS, label và value, đến nhập liệu trong SPSS.
Đây là kỹ năng nền tảng, quyết định chất lượng toàn bộ quá trình phân tích dữ liệu. Để học sâu hơn về SPSS và thống kê ứng dụng, bạn có thể tham khảo thêm các bài hướng dẫn tại xulysolieu.info – Xử lý số liệu.
SPSS cho Mac: Cách cài đặt và sử dụng chi tiết dành cho người mới
SPSS cho Mac là lựa chọn phổ biến của sinh viên, giảng viên và người làm phân tích dữ liệu sử dụng hệ điều hành macOS. Tuy nhiên, do quy trình cài đặt trên MacOS khác Windows, nhiều người mới thường gặp khó khăn khi bắt đầu với SPSS cho Mac. Bài viết này từ xulysolieu.info – Xử lý số liệu sẽ hướng dẫn bạn từng bước cài đặt SPSS MacBook, từ khâu tải phần mềm đến cách sử dụng SPSS trên Mac một cách hiệu quả.
1. SPSS là gì?
Trước khi tìm hiểu chi tiết SPSS cho Mac, bạn cần nắm rõ SPSS là gì. SPSS (Statistical Package for the Social Sciences) là phần mềm thống kê SPSS chuyên dùng để xử lý và phân tích dữ liệu. SPSS được sử dụng rộng rãi trong nghiên cứu khoa học, kinh tế, marketing, giáo dục và khoa học xã hội.
Với giao diện trực quan, thao tác dựa trên menu và hộp thoại, SPSS cho Mac phù hợp cả với người mới bắt đầu học phân tích dữ liệu.
2. Vì sao nên sử dụng SPSS cho Mac?
Hiện nay, IBM đã tối ưu SPSS cho Mac để hoạt động ổn định trên macOS, bao gồm cả chip Apple Silicon. Người dùng MacBook hoàn toàn có thể yên tâm khi sử dụng SPSS trên Mac cho học tập và nghiên cứu.
- Hỗ trợ đầy đủ các phân tích thống kê phổ biến
- Giao diện nhất quán giữa macOS và Windows
- Tương thích tốt với SPSS Mac M1 và SPSS Mac M2
- Xử lý dữ liệu nhanh, ổn định
3. Chuẩn bị trước khi cài đặt SPSS cho MacBook
Trước khi tiến hành cài đặt SPSS MacBook, bạn cần kiểm tra một số điều kiện cơ bản:
- MacBook chạy macOS từ Catalina trở lên
- Dung lượng trống tối thiểu 5GB
- Quyền quản trị (administrator)
- Mã bản quyền SPSS hợp lệ
Đối với máy dùng chip Apple Silicon, bạn nên ưu tiên phiên bản mới để đảm bảo SPSS Mac M1 và SPSS Mac M2 hoạt động ổn định.
4. Tải SPSS cho Mac
Bước đầu tiên trong quá trình sử dụng SPSS cho Mac là tải bộ cài đặt. Bạn nên tải SPSS cho Mac từ nguồn chính thức để tránh lỗi và rủi ro bảo mật.
Các bước thực hiện:
- Truy cập trang tải SPSS của IBM
- Đăng nhập hoặc tạo tài khoản IBM
- Chọn phiên bản SPSS phù hợp với macOS
- Tải file cài đặt (thường ở định dạng .zip hoặc .dmg)
Lưu ý: các phiên bản SPSS từ 26 trở lên tương thích tốt với macOS mới, đặc biệt là SPSS cho Mac chạy chip M1 và M2.
5. Hướng dẫn cài đặt SPSS cho MacBook từng bước
Bước 1: Giải nén bộ cài
Sau khi tải SPSS cho Mac, mở thư mục Downloads và giải nén file cài đặt.
Bước 2: Chạy file cài đặt
Mở thư mục vừa giải nén, tìm file cài đặt có đuôi .pkg và nhấp đúp để khởi chạy trình cài đặt SPSS cho Mac.
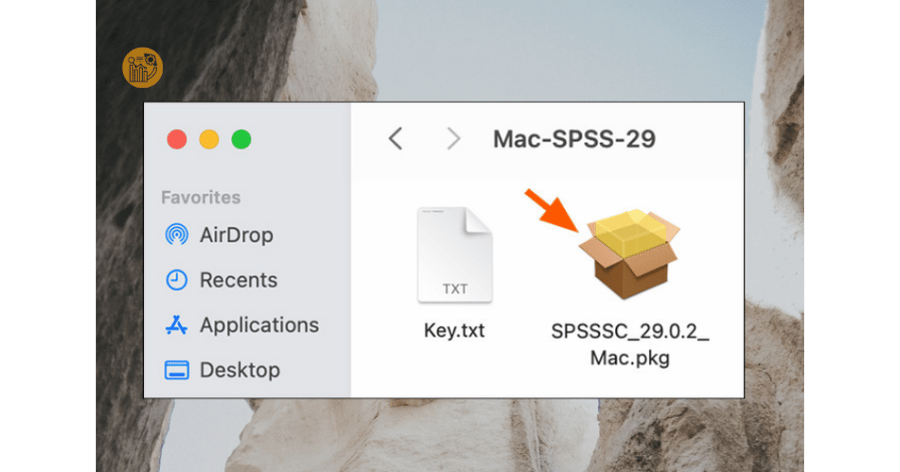
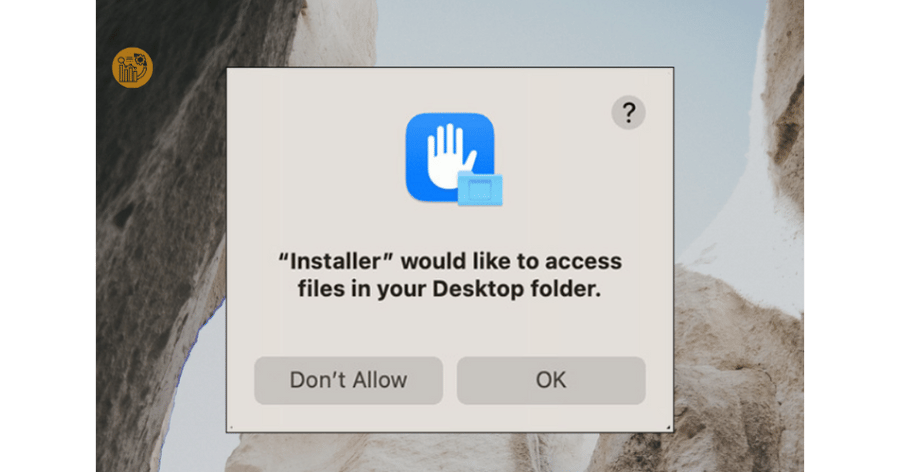
Nhấn “OK”
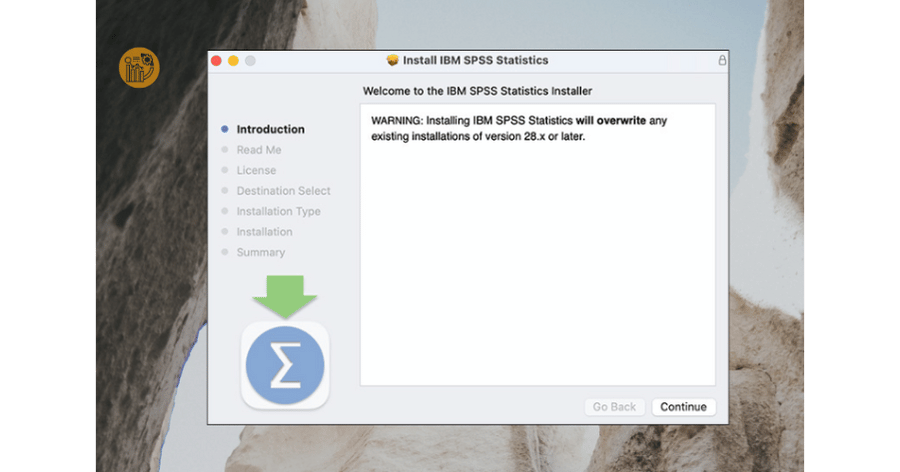
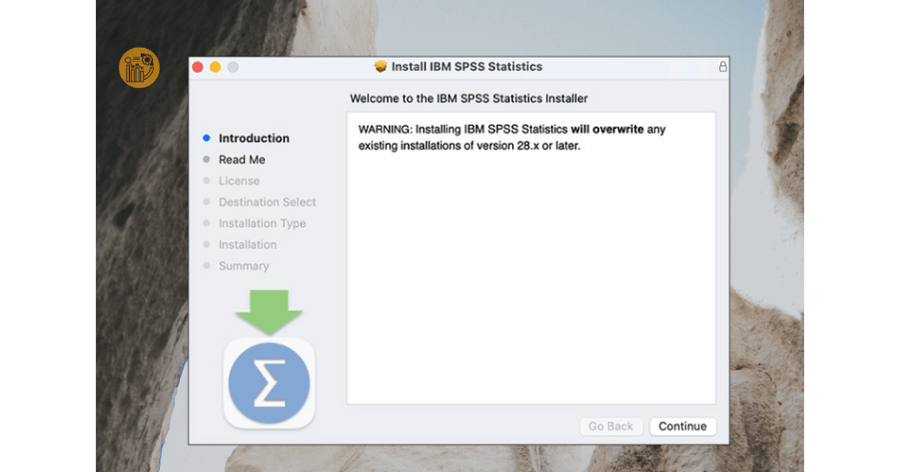
Bước 3: Xác nhận cài đặt
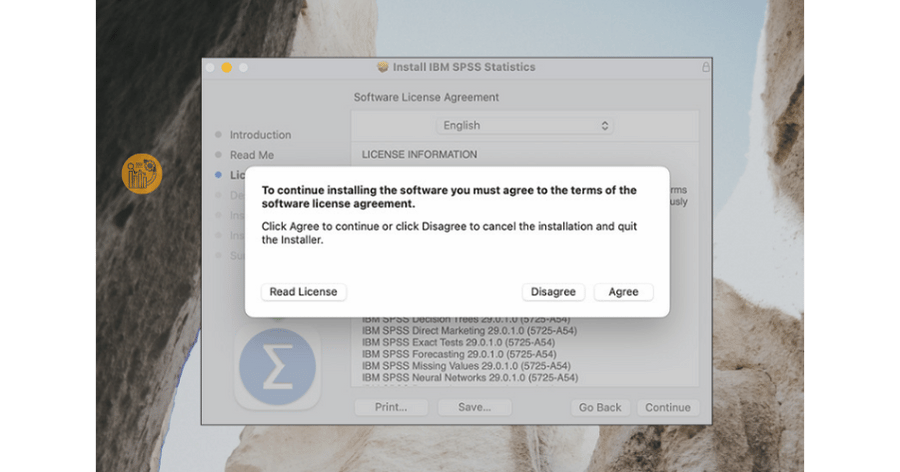
Nhấn Continue qua các màn hình giới thiệu, đọc điều khoản và chọn Agree để đồng ý. Giữ nguyên thư mục cài đặt mặc định để tránh lỗi khi sử dụng SPSS trên Mac.
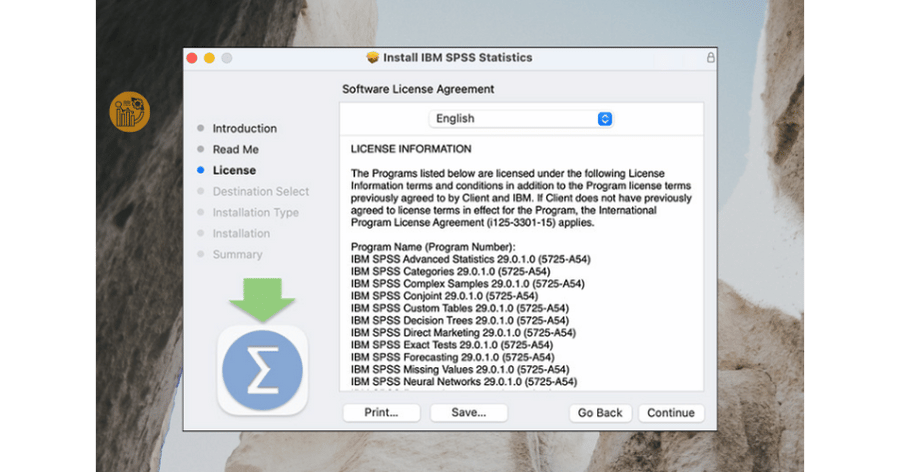
Nhấn “Agree”
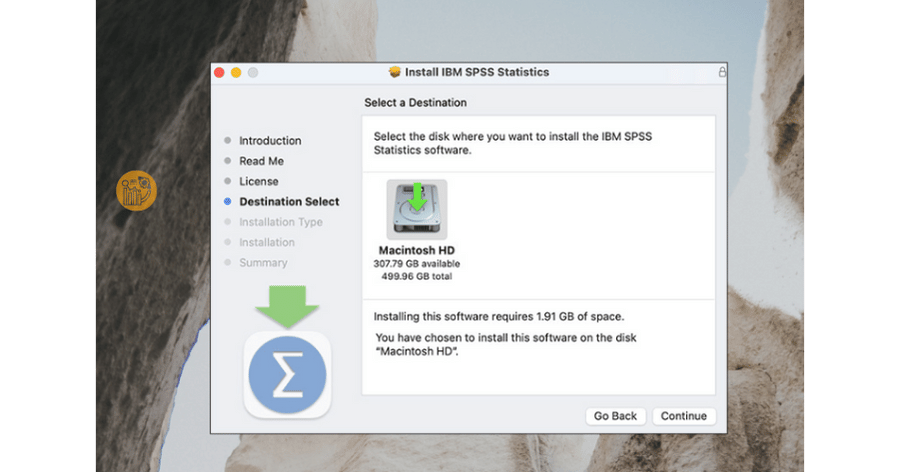
Giữ nguyên vị trí mặc định, nhấn “Continue”
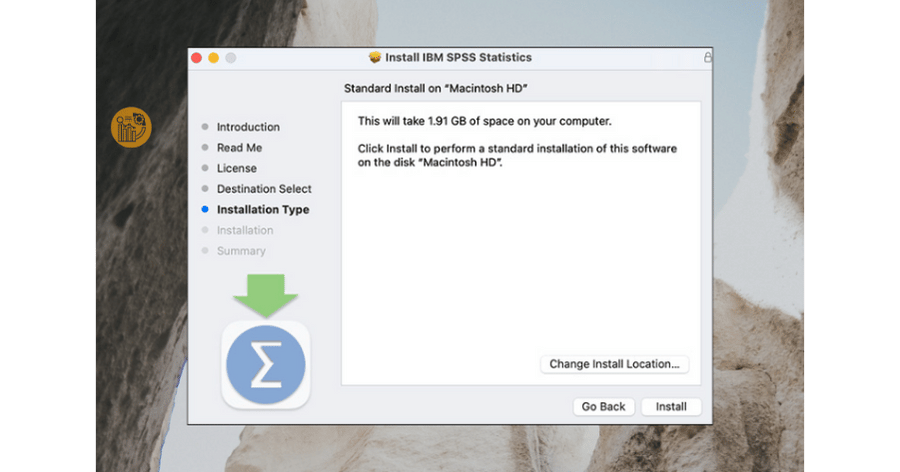
Nhấn Install để bắt đầu cài đặt
Bước 4: Nhập quyền quản trị
Nhập mật khẩu quản trị hoặc xác thực Touch ID để hệ thống tiến hành cài đặt SPSS MacBook.
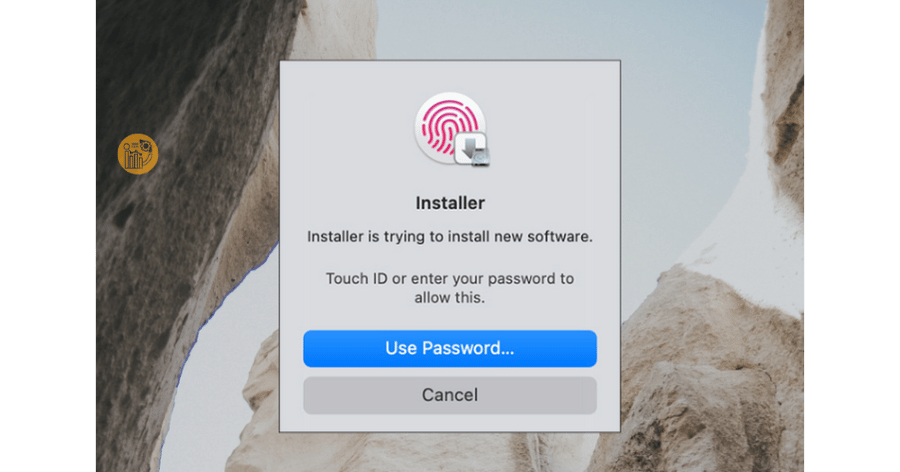
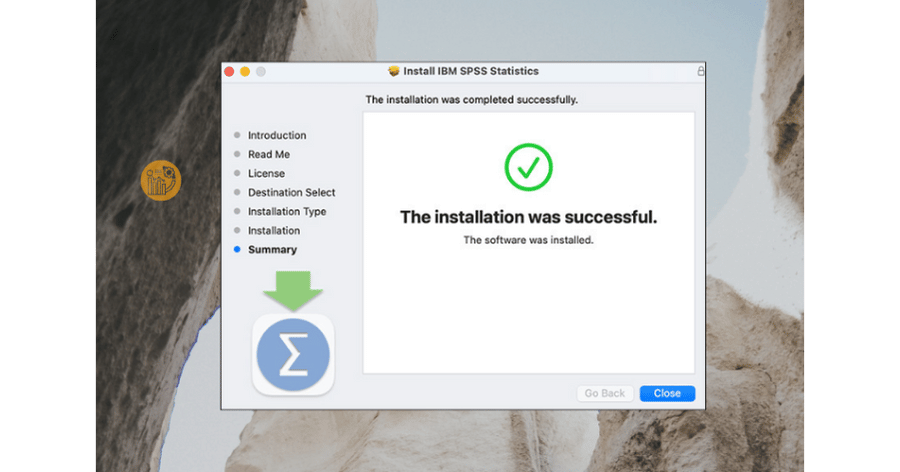
Bước 5: Hoàn tất cài đặt
Khi cài đặt xong, hệ thống sẽ thông báo hoàn tất. Lúc này, bạn đã cài xong SPSS cho Mac.
6. Kích hoạt bản quyền SPSS cho Mac
Sau khi cài đặt, bạn cần kích hoạt bản quyền để sử dụng SPSS trên Mac đầy đủ chức năng.
1. Mở IBM SPSS Statistics trong thư mục Applications
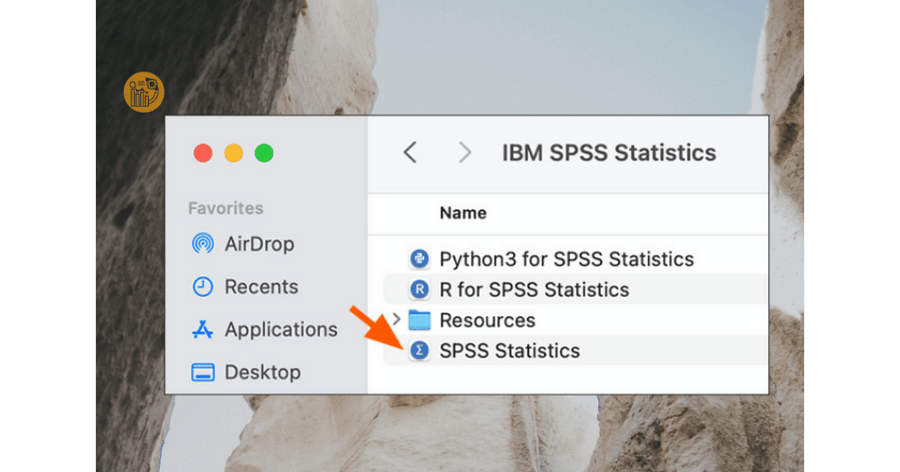
2. Khởi chạy License Authorization Wizard

3. Chọn Authorized User License
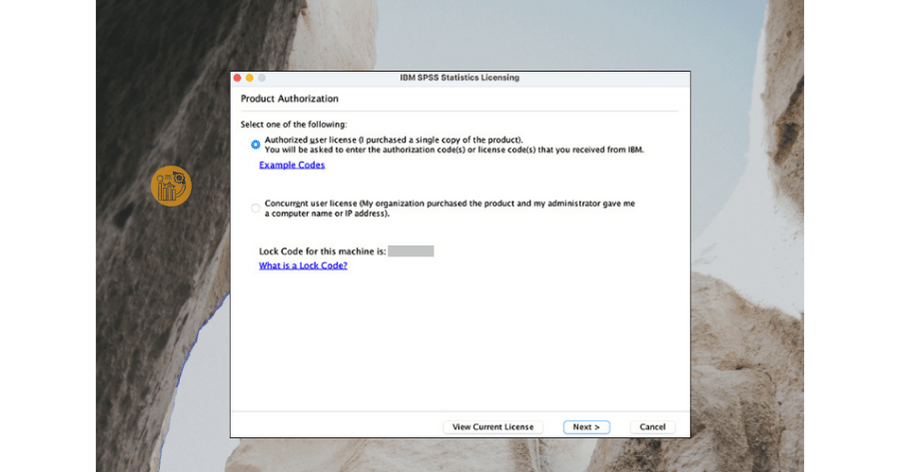
4. Nếu hợp lệ, nhấn Next
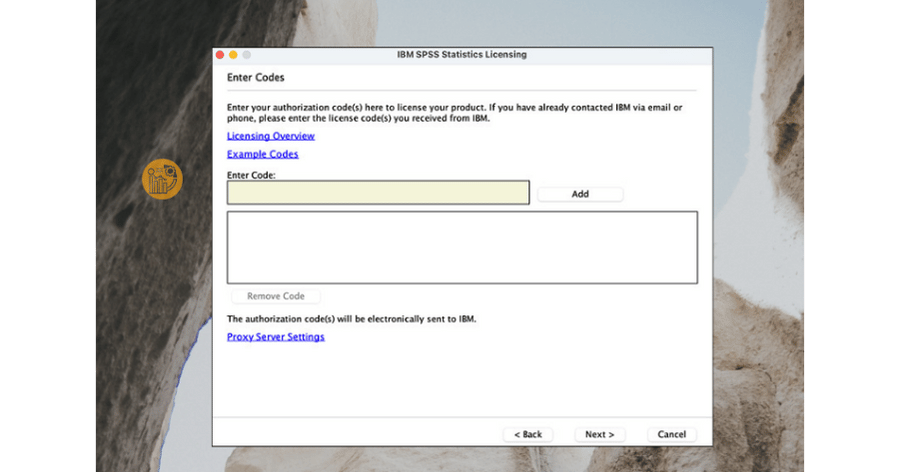
5. Xác nhận và hoàn tất
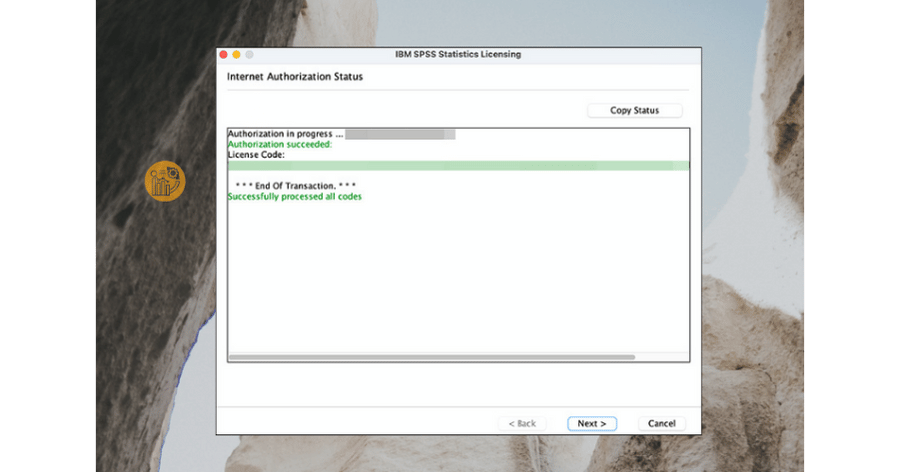
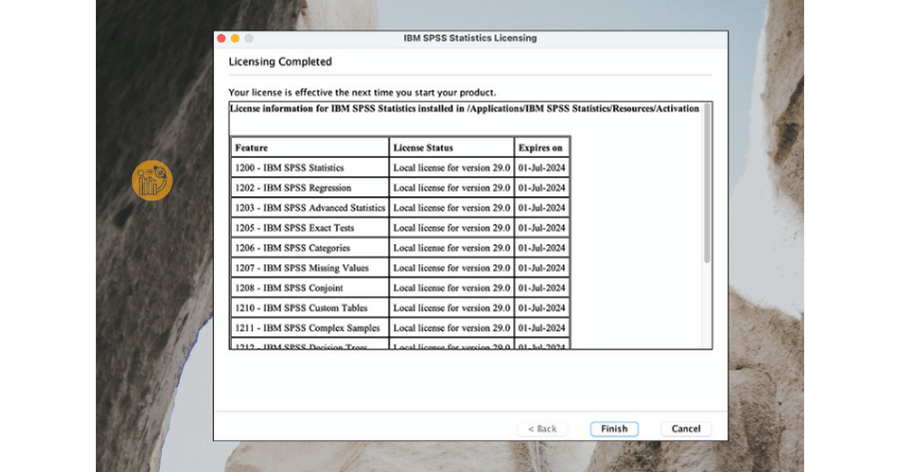
Khi kích hoạt thành công, bạn có thể sử dụng phần mềm thống kê SPSS mà không bị giới hạn.
7. Sử dụng SPSS trên Mac cho người mới
Sau khi hoàn tất cài đặt SPSS cho Mac, bạn có thể bắt đầu làm quen với giao diện và chức năng cơ bản.
- Variable View: khai báo biến
- Data View: nhập dữ liệu
- Analyze: thực hiện phân tích thống kê
Việc sử dụng SPSS trên Mac không khác nhiều so với Windows, giúp người học dễ dàng chuyển đổi môi trường làm việc.
8. Lưu ý khi dùng SPSS trên Mac M1 và Mac M2
Đối với SPSS Mac M1 và SPSS Mac M2, bạn nên:
- Sử dụng phiên bản SPSS mới nhất
- Cập nhật macOS thường xuyên
- Không cài song song nhiều phiên bản SPSS
Các lưu ý này giúp SPSS cho Mac hoạt động ổn định và tránh lỗi phát sinh.
9. Tổng kết
Qua bài viết này, bạn đã nắm được cách tải SPSS cho Mac, cài đặt SPSS MacBook và sử dụng SPSS trên Mac một cách bài bản. Việc làm chủ SPSS cho Mac là bước quan trọng đối với người học phân tích dữ liệu và nghiên cứu khoa học.
Để tiếp tục nâng cao kỹ năng với phần mềm thống kê SPSS, bạn có thể tham khảo thêm các bài hướng dẫn chuyên sâu tại xulysolieu.info – Xử lý số liệu.
Công thức hồi quy tuyến tính và cách sử dụng cơ bản
Trong lĩnh vực phân tích dữ liệu và khoa học dữ liệu, công thức hồi quy tuyến tính là một trong những khái niệm nền tảng và được sử dụng phổ biến nhất. Nhờ sự đơn giản, dễ diễn giải và khả năng áp dụng tốt với nhiều bài toán thực tế, công thức hồi quy tuyến tính thường là lựa chọn đầu tiên khi bắt đầu xây dựng mô hình hồi quy.
Bài viết này của xulysolieu.info – Xử lý số liệu sẽ trình bày một cách hệ thống về công thức hồi quy tuyến tính, từ lý thuyết toán học, ý nghĩa các thành phần cho đến cách áp dụng trong dự báo dữ liệu rời rạc.
1. Tổng quan về hồi quy tuyến tính
Hồi quy tuyến tính là phương pháp mô hình hóa mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập thông qua một phương trình tuyến tính. Về bản chất, công thức hồi quy tuyến tính mô tả xu hướng trung bình của dữ liệu và cho phép dự đoán giá trị của biến phụ thuộc khi biết biến độc lập.
Tùy theo số lượng biến độc lập, hồi quy tuyến tính được chia thành:
- Hồi quy tuyến tính đơn: chỉ có một biến độc lập.
- Hồi quy tuyến tính bội: có từ hai biến độc lập trở lên.
Dù là hồi quy tuyến tính đơn hay hồi quy tuyến tính bội, nền tảng toán học vẫn xoay quanh cùng một công thức hồi quy tuyến tính.
2. Công thức hồi quy tuyến tính cơ bản
Trong trường hợp đơn giản nhất, hồi quy tuyến tính đơn được biểu diễn bởi phương trình:
y = ax + b
Trong đó:
- y: biến phụ thuộc (giá trị cần dự báo).
- x: biến độc lập.
- a: hệ số hồi quy, thể hiện mức độ ảnh hưởng của x lên y.
- b: hệ số chặn (intercept).
Đây chính là công thức hồi quy tuyến tính phổ biến nhất, thường xuất hiện trong các giáo trình thống kê và phân tích dữ liệu.
Mục tiêu của bài toán hồi quy là ước lượng hệ số a và b sao cho phương trình hồi quy mô tả dữ liệu tốt nhất.
3. Biểu diễn ma trận của công thức hồi quy tuyến tính
Với tập dữ liệu gồm N quan sát, ta có thể viết công thức hồi quy tuyến tính dưới dạng ma trận:
y = Xw
Trong đó:
- y: vector giá trị biến phụ thuộc.
- X: ma trận dữ liệu gồm cột hằng số 1 và các biến độc lập.
- w: vector hệ số cần ước lượng.
Việc biểu diễn này giúp mở rộng công thức hồi quy tuyến tính sang hồi quy tuyến tính bội và thuận tiện cho việc tính toán bằng máy tính.
4. Nguyên lý ước lượng hệ số trong hồi quy tuyến tính
Trong thực tế, các điểm dữ liệu hiếm khi nằm hoàn toàn trên một đường thẳng. Do đó, công thức hồi quy tuyến tính được xây dựng dựa trên nguyên lý bình phương tối thiểu (Least Squares).
Ý tưởng chính là tìm bộ hệ số w sao cho tổng bình phương sai số giữa giá trị thực tế và giá trị dự báo là nhỏ nhất.
Nghiệm của bài toán này được xác định bởi công thức:
w = (XᵀX)⁻¹Xᵀy Đây là dạng tổng quát và quan trọng nhất của công thức hồi quy tuyến tính, được sử dụng trong cả hồi quy tuyến tính đơn và hồi quy tuyến tính bội.
5. Ý nghĩa của biến độc lập và biến phụ thuộc

Khi áp dụng công thức hồi quy tuyến tính, việc xác định đúng biến độc lập và biến phụ thuộc là yếu tố then chốt.
Biến độc lập là nguyên nhân hoặc yếu tố tác động, trong khi biến phụ thuộc là kết quả hoặc đại lượng cần dự báo. Một mô hình hồi quy chỉ có ý nghĩa khi mối quan hệ giữa các biến phù hợp với giả định tuyến tính.
6. Ứng dụng công thức hồi quy tuyến tính trong dự báo
Trong bài toán dự báo lưu lượng xả lũ, mực nước hồ được xem là biến độc lập, còn lưu lượng xả là biến phụ thuộc. Thông qua dữ liệu lịch sử, ta xây dựng công thức hồi quy tuyến tính để ước lượng lượng nước cần xả tương ứng với mỗi mức nước.
Ưu điểm của cách tiếp cận này là:
- Dễ triển khai và tính toán.
- Giải thích rõ ràng mối quan hệ giữa các biến.
- Hiệu quả với dữ liệu tuyến tính và ít nhiễu.
So với các thuật toán tối ưu như GA, PSO hay ACO, công thức hồi quy tuyến tính cho nghiệm xác định, không phụ thuộc vào khởi tạo ngẫu nhiên.
7. Hạn chế của mô hình hồi quy tuyến tính
Dù rất hữu ích, công thức hồi quy tuyến tính vẫn tồn tại những hạn chế nhất định:
- Nhạy cảm với dữ liệu nhiễu và ngoại lệ.
- Không mô tả được các quan hệ phi tuyến phức tạp.
- Giả định mối quan hệ tuyến tính có thể không phù hợp với mọi bài toán.
Do đó, trong thực tế, hồi quy tuyến tính thường được dùng như bước phân tích ban đầu trước khi áp dụng các mô hình nâng cao hơn.
8. Nhận xét và kết luận
Công thức hồi quy tuyến tính là nền tảng quan trọng trong thống kê, kinh tế lượng và khoa học dữ liệu. Với cách tiếp cận rõ ràng, dễ hiểu và khả năng áp dụng rộng rãi, mô hình hồi quy tuyến tính giúp người học nhanh chóng nắm bắt tư duy phân tích dữ liệu.
Trong các bài toán có mối quan hệ gần tuyến tính, công thức hồi quy tuyến tính thường mang lại hiệu quả cao hơn nhiều phương pháp tối ưu phức tạp. Đây cũng là lý do vì sao hồi quy tuyến tính luôn được giảng dạy sớm trong các chương trình đào tạo về phân tích dữ liệu.
Standard Deviation – STDEV là gì? Ý nghĩa, Công thức và cách áp dụng trong thống kê
Trong phân tích dữ liệu, stdev là gì là một trong những câu hỏi nền tảng mà bất kỳ người học thống kê nào cũng cần nắm vững. STDEV, hay còn gọi là Standard Deviation – độ lệch chuẩn, xuất hiện rất thường xuyên trong thống kê mô tả, phân tích dữ liệu, cũng như khi làm việc với các công cụ như Excel hay SPSS. Bài viết này sẽ giúp bạn hiểu rõ stdev là gì, ý nghĩa độ lệch chuẩn, cách diễn giải và cách áp dụng trong thực tế phân tích dữ liệu.
1. STDEV là gì?
STDEV là gì? STDEV là viết tắt của Standard Deviation, trong tiếng Việt gọi là độ lệch chuẩn. Độ lệch chuẩn dùng để đo lường mức độ phân tán dữ liệu xung quanh giá trị trung bình. Nói cách khác, khi tìm hiểu stdev là gì, bạn đang tìm cách trả lời câu hỏi: các giá trị trong tập dữ liệu có “tập trung” hay “trải rộng” quanh trung bình đến mức nào.
Nếu các giá trị nằm rất gần trung bình, độ lệch chuẩn nhỏ. Ngược lại, nếu các giá trị nằm rải rác xa trung bình, độ lệch chuẩn lớn. Đây là lý do vì sao standard deviation đóng vai trò quan trọng trong thống kê mô tả.
2. Ý nghĩa của độ lệch chuẩn trong phân tích dữ liệu
Hiểu stdev là gì chưa đủ, điều quan trọng hơn là hiểu ý nghĩa độ lệch chuẩn. Độ lệch chuẩn cho biết mức độ ổn định hay biến động của dữ liệu.
- STDEV nhỏ: dữ liệu ổn định, các giá trị ít biến động.
- STDEV lớn: dữ liệu biến động mạnh, có thể tồn tại giá trị ngoại lai.
Trong phân tích dữ liệu thực tế (điểm thi, doanh thu, thời gian xử lý…), việc hiểu stdev là gì giúp nhà phân tích đánh giá rủi ro, độ tin cậy và tính nhất quán của dữ liệu.
3. STDEV trong thống kê mô tả
Trong thống kê mô tả, độ lệch chuẩn thường đi kèm với các chỉ số như giá trị trung bình (mean), trung vị (median), min và max. Khi học stdev là gì, bạn nên đặt nó trong bối cảnh tổng thể của thống kê mô tả.
Ví dụ:
- Tập A: 4, 4, 4, 4 → mean = 4, STDEV = 0
- Tập B: 1, 4, 7, 10 → mean = 5.5, STDEV lớn hơn
Qua ví dụ trên, có thể thấy rõ phân tán dữ liệu ở tập B lớn hơn, do đó độ lệch chuẩn cao hơn. Đây là cách trực quan để hiểu stdev là gì.
4. Công thức Standard Deviation (tham khảo)
Trong nhiều trường hợp ứng dụng, người học không cần tính toán thủ công, nhưng để hiểu sâu stdev là gì, bạn nên nắm công thức cơ bản.
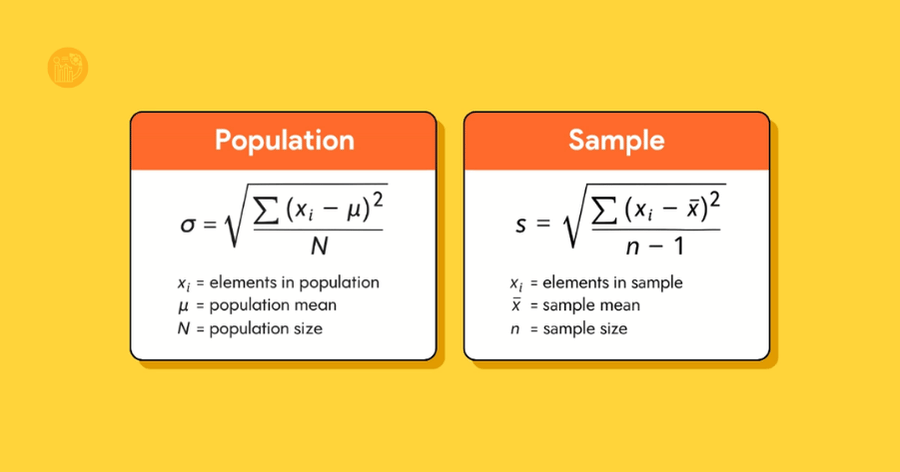
4.1. Độ lệch chuẩn tổng thể (Population Standard Deviation)
σ = √( Σ(xᵢ − μ)² / N )
4.2. Độ lệch chuẩn mẫu (Sample Standard Deviation)
s = √( Σ(xᵢ − x̄)² / (n − 1) )
Trong đó:
- xᵢ: giá trị quan sát
- μ hoặc x̄: giá trị trung bình
- N, n: số quan sát
Khi làm phân tích thực tế, bạn sẽ thường gặp stdev trong excel hoặc stdev trong spss thay vì tự tính tay.
5. STDEV trong Excel
Khi làm việc với bảng tính, nhiều người tiếp cận khái niệm stdev là gì thông qua Excel. Excel cung cấp các hàm phổ biến như:
- STDEV.S: tính độ lệch chuẩn mẫu
- STDEV.P: tính độ lệch chuẩn tổng thể
Việc sử dụng stdev trong excel giúp người phân tích nhanh chóng đánh giá mức độ phân tán dữ liệu mà không cần xử lý thủ công.
6. STDEV trong SPSS
Trong nghiên cứu khoa học và phân tích dữ liệu chuyên sâu, stdev trong spss là chỉ số gần như luôn xuất hiện trong bảng thống kê mô tả.
SPSS tự động tính độ lệch chuẩn khi người dùng chạy Descriptive Statistics. Điều quan trọng không chỉ là biết stdev là gì, mà còn là biết cách diễn giải con số này trong bối cảnh nghiên cứu.
7. Cách diễn giải Standard Deviation đúng cách
Nhiều người hiểu stdev là gì nhưng lại diễn giải sai. Một số nguyên tắc cơ bản:
- Không so sánh STDEV giữa các biến có đơn vị đo khác nhau.
- Luôn xem STDEV cùng với mean.
- STDEV lớn không phải lúc nào cũng xấu, mà chỉ phản ánh sự biến động.
Đây là điểm then chốt trong việc hiểu ý nghĩa độ lệch chuẩn.
8. Ứng dụng của STDEV trong thực tế
Khi đã hiểu stdev là gì, bạn sẽ thấy độ lệch chuẩn được ứng dụng rất rộng:
- Đánh giá độ ổn định của điểm số học sinh
- Phân tích rủi ro tài chính
- So sánh hiệu suất giữa các nhóm
- Kiểm tra mức độ biến động của dữ liệu khảo sát
Tại xulysolieu.info – Xử lý số liệu, độ lệch chuẩn luôn được xem là chỉ số nền tảng trong mọi bài toán phân tích dữ liệu.
9. Tổng kết
Qua bài viết này, bạn đã nắm được stdev là gì, hiểu rõ standard deviation dùng để làm gì, ý nghĩa độ lệch chuẩn trong thống kê mô tả, cũng như cách áp dụng stdev trong excel và stdev trong spss.
Việc hiểu đúng và sử dụng đúng độ lệch chuẩn sẽ giúp bạn nâng cao năng lực phân tích dữ liệu một cách bài bản và khoa học. Để học sâu hơn về các khái niệm thống kê và ứng dụng thực tế, bạn có thể tham khảo thêm các bài viết chuyên môn tại xulysolieu.info.
Kiểm định giả thuyết (Hypothesis Testing): Khái niệm, quy trình và cách đưa ra kết luận thống kê
Kiểm định giả thuyết là một bước không thể thiếu trong thống kê suy luận, giúp các nhà nghiên cứu và phân tích dữ liệu đưa ra kết luận dựa trên bằng chứng thực nghiệm thay vì cảm tính. Trong bài viết này, Xử lý số liệu sẽ giúp bạn hiểu rõ hypothesis testing là gì, quy trình thực hiện, cách xác định mức ý nghĩa alpha và làm thế nào để hạn chế sai lầm loại I và loại II khi thực hiện kiểm định thống kê SPSS.
1. Kiểm định giả thuyết là gì?
Kiểm định giả thuyết (tiếng Anh: Hypothesis Testing) là quá trình sử dụng các công cụ và tiêu chuẩn thống kê để kiểm tra xem một giả thuyết về tổng thể có được dữ liệu mẫu ủng hộ hay không. Mục tiêu là giúp người phân tích đưa ra quyết định dựa trên xác suất thống kê thay vì phán đoán chủ quan.
Trong kiểm định giả thuyết, có hai giả thuyết được đưa ra:
- Giả thuyết không (H0): là giả định ban đầu, thường thể hiện rằng “không có sự khác biệt” hoặc “không có mối quan hệ”.
- Giả thuyết đối (H1): là giả thuyết mà nhà nghiên cứu muốn chứng minh – tức có sự khác biệt hoặc có mối quan hệ giữa các biến.
Ví dụ: Khi nghiên cứu mối quan hệ giữa quy mô doanh nghiệp và mức thù lao trung bình của hội đồng quản trị, ta có thể đặt:
- H0: Thù lao trung bình của hội đồng quản trị là như nhau giữa các doanh nghiệp lớn và nhỏ.
- H1: Thù lao trung bình của hội đồng quản trị ở doanh nghiệp lớn cao hơn doanh nghiệp nhỏ.
Việc chấp nhận hay bác bỏ H0 dựa trên kết quả phân tích dữ liệu mẫu và mức ý nghĩa alpha đã chọn.
2. Quy trình kiểm định giả thuyết

Để hiểu trọn vẹn quy trình kiểm định giả thuyết, ta có thể chia thành 5 bước cơ bản:
Bước 1: Xây dựng giả thuyết
Đặt H0 và H1 dựa trên vấn đề nghiên cứu. H0 là mặc định “không có thay đổi”, H1 là giả định ngược lại.
Bước 2: Xác định mức ý nghĩa (α)
Mức ý nghĩa alpha (ký hiệu α) là xác suất chấp nhận rủi ro khi bác bỏ H0 dù H0 đúng. Thông thường, α = 0.05 (tức 5% rủi ro sai lầm loại I). Một số nghiên cứu nghiêm ngặt hơn chọn α = 0.01 hoặc α = 0.10 tùy mục tiêu.
Bước 3: Chọn kiểm định thống kê phù hợp
Tùy loại dữ liệu và mục tiêu phân tích, bạn có thể chọn các kiểm định khác nhau:
- T-Test: so sánh giá trị trung bình giữa hai nhóm (phổ biến trong kiểm định thống kê SPSS).
- Chi-Square: kiểm định mối quan hệ giữa hai biến định tính.
- ANOVA: so sánh giá trị trung bình giữa nhiều nhóm.
Bước 4: Tính toán và xác định giá trị p-value
P-value là xác suất cho biết mức độ phù hợp của dữ liệu với giả thuyết H0. Nếu p-value nhỏ hơn mức ý nghĩa α, ta bác bỏ H0.
Bước 5: Đưa ra kết luận
Khi kết quả phân tích cho thấy sự khác biệt có ý nghĩa thống kê, ta có thể kết luận rằng dữ liệu ủng hộ H1. Nếu không, ta giữ H0 và cho rằng chưa có đủ bằng chứng để bác bỏ nó.
3. Sai lầm loại I và loại II trong kiểm định giả thuyết
Trong quá trình kiểm định giả thuyết, có hai loại sai lầm thường gặp:
- Sai lầm loại I (Type I Error): Bác bỏ giả thuyết H0 dù nó đúng. Xác suất xảy ra sai lầm này chính là mức ý nghĩa alpha.
- Sai lầm loại II (Type II Error): Không bác bỏ H0 dù nó sai. Xác suất xảy ra sai lầm này thường ký hiệu là β.
Để loại bỏ sai lầm loại 1 và loại 2, nhà nghiên cứu cần:
- Chọn kích thước mẫu đủ lớn để giảm sai lầm loại II.
- Chọn mức α phù hợp để cân bằng giữa độ nhạy và độ tin cậy của kiểm định.
- Sử dụng đúng loại kiểm định theo bản chất dữ liệu.
4. Ví dụ kiểm định giả thuyết trong thực tế
Giả sử bạn muốn kiểm tra xem mức thù lao trung bình của hội đồng quản trị có khác nhau giữa các doanh nghiệp lớn và nhỏ không. Dữ liệu được nhập vào SPSS và bạn chọn T-Test độc lập.
Kết quả SPSS trả về giá trị p-value = 0.03 và mức ý nghĩa α = 0.05. Vì p-value < α, ta bác bỏ H0 và kết luận: “Thù lao trung bình của hội đồng quản trị tại các doanh nghiệp lớn cao hơn đáng kể so với doanh nghiệp nhỏ.”
Ví dụ này cho thấy cách áp dụng kiểm định giả thuyết trong kiểm định thống kê SPSS để đưa ra kết luận có cơ sở.
5. Ứng dụng của kiểm định giả thuyết trong phân tích dữ liệu

Kiểm định giả thuyết là công cụ nền tảng trong các nghiên cứu định lượng, đặc biệt trong:
- Kinh tế học ứng dụng: đánh giá tác động của chính sách, giá trị trung bình, hay sự khác biệt giữa các nhóm dân số.
- Marketing: kiểm định hành vi tiêu dùng, mức độ hài lòng khách hàng.
- Y học và khoa học xã hội: xác định hiệu quả điều trị, so sánh nhóm đối chứng và nhóm thử nghiệm.
6. Cách hiểu đúng mức ý nghĩa alpha
Nhiều người lầm tưởng rằng α là “xác suất giả thuyết sai”. Thực tế, α chỉ thể hiện xác suất phạm sai lầm loại I – tức bác bỏ H0 đúng. Khi p-value nhỏ hơn α, điều này không có nghĩa H1 chắc chắn đúng mà chỉ là bằng chứng đủ mạnh để nghiêng về H1.
Ví dụ: α = 0.05 nghĩa là bạn chấp nhận 5% rủi ro khi bác bỏ một giả thuyết đúng. Đây là ngưỡng được sử dụng phổ biến trong thống kê, kể cả khi thực hiện kiểm định thống kê SPSS.
7. Kết luận
Qua bài viết này, xulysolieu.info đã giúp bạn hiểu rõ kiểm định giả thuyết là gì, quy trình kiểm định giả thuyết, và cách đưa ra kết luận thống kê chính xác. Việc nắm vững mức ý nghĩa alpha, biết cách hạn chế sai lầm loại I và loại II, cùng việc áp dụng kiểm định thống kê SPSS đúng phương pháp sẽ giúp bạn tự tin hơn trong mọi nghiên cứu định lượng.
Tóm lại, kiểm định giả thuyết không chỉ là công cụ thống kê mà còn là nền tảng giúp biến dữ liệu thành bằng chứng xác đáng. Hãy thực hành thường xuyên trên SPSS và các phần mềm xử lý dữ liệu khác để hiểu sâu hơn về sức mạnh của hypothesis testing trong khoa học dữ liệu.
Phương sai của sai số thay đổi là gì? Cách phát hiện và khắc phục hiện tượng Heteroskedasticity bằng Stata
Trong phân tích hồi quy, phương sai của sai số thay đổi là một trong những hiện tượng phổ biến nhưng dễ bị bỏ qua, đặc biệt khi người phân tích chưa kiểm tra kỹ các giả định của mô hình. Bài viết này của Xử lý số liệu sẽ giúp bạn hiểu rõ heteroskedasticity là gì, cách phát hiện và khắc phục phương sai thay đổi bằng phần mềm Stata một cách hiệu quả.
1. Phương sai của sai số thay đổi là gì?
Trong mô hình hồi quy tuyến tính cổ điển, giả định rằng các sai số (residuals) có phương sai không đổi — hay còn gọi là hiện tượng homoscedasticity. Điều này có nghĩa là mức độ biến động của phần sai số là giống nhau tại mọi giá trị của biến độc lập.
Tuy nhiên, trong thực tế, giả định này thường không được thỏa mãn. Khi phương sai của sai số thay đổi theo giá trị của biến độc lập, ta nói mô hình xuất hiện hiện tượng phương sai thay đổi hay heteroskedasticity. Nói cách khác, các sai số không còn có cùng mức biến động ở mọi quan sát, dẫn đến sự sai lệch trong việc ước lượng sai số chuẩn và kiểm định thống kê.
Hiện tượng phương sai của sai số thay đổi không làm cho ước lượng OLS bị thiên lệch, nhưng nó khiến các ước lượng không còn hiệu quả — tức là không còn là các ước lượng tuyến tính không thiên lệch tốt nhất (BLUE). Khi đó, các kiểm định t và F trong hồi quy có thể cho kết quả sai lệch, ảnh hưởng đến kết luận của nghiên cứu.
2. Dấu hiệu của phương sai của sai số thay đổi
Một mô hình bị phương sai của sai số thay đổi thường thể hiện qua việc phần dư (residuals) phân tán không đều khi vẽ đồ thị phần dư theo giá trị dự báo. Nếu các điểm phần dư có xu hướng tạo thành hình phễu (hẹp ở đầu, loe ra ở cuối), đây là dấu hiệu điển hình của heteroskedasticity.
3. Cách phát hiện phương sai thay đổi trong Stata
Trong Stata, có hai phương pháp phổ biến để kiểm định phương sai thay đổi trong mô hình hồi quy OLS: kiểm định White và kiểm định Breusch-Pagan.
Cách 1: Kiểm định White
Kiểm định White giúp kiểm tra xem phần sai số có phương sai đồng nhất hay không. Cú pháp thực hiện trong Stata như sau:
estat imtestNếu kết quả cho ra p-value < 0.05, ta bác bỏ giả thuyết H0: “Phương sai của sai số không đổi”. Khi đó, kết luận rằng mô hình có phương sai của sai số thay đổi.
Cách 2: Kiểm định Breusch–Pagan
Kiểm định Breusch–Pagan cũng được dùng phổ biến để phát hiện phương sai thay đổi. Trong Stata, sử dụng lệnh:
estat hettestTương tự, nếu p-value < 0.05, ta kết luận rằng tồn tại heteroskedasticity. Nếu p-value > 0.05, mô hình có phương sai không đổi — điều kiện mong muốn trong hồi quy tuyến tính.
4. Kiểm định phương sai thay đổi trong dữ liệu bảng (Panel Data)
Khi làm việc với dữ liệu bảng, cần áp dụng các kiểm định phù hợp với mô hình hiệu ứng cố định (FEM) hoặc hiệu ứng ngẫu nhiên (REM).
Phương sai thay đổi trong mô hình REM
Dùng lệnh kiểm định LM – Breusch và Pagan Lagrangian Multiplier:
xttest0Nếu p-value < 0.05, bác bỏ giả thuyết H0: “Phương sai qua các thực thể là không đổi”, tức là có phương sai của sai số thay đổi.
Phương sai thay đổi trong mô hình FEM
Sử dụng kiểm định Wald bằng lệnh sau (phải cài đặt trước):
ssc install xttest3
xttest3Nếu p-value < 0.05, cũng kết luận rằng tồn tại phương sai của sai số thay đổi giữa các thực thể trong mô hình.
5. Cách khắc phục phương sai của sai số thay đổi
Sau khi phát hiện mô hình có phương sai của sai số thay đổi, cần khắc phục để đảm bảo tính chính xác của các ước lượng và kiểm định. Có hai cách phổ biến:
5.1. Sử dụng sai số chuẩn hiệu chỉnh (Robust Standard Errors)
Đây là phương pháp đơn giản và hiệu quả nhất. Stata cung cấp tùy chọn robust giúp điều chỉnh sai số chuẩn sao cho phù hợp với trường hợp có heteroskedasticity.
Ví dụ:
regress y x1 x2 x3, robustLệnh này sẽ giúp mô hình hồi quy được ước lượng với sai số chuẩn hiệu chỉnh, giúp các kiểm định t và F trở nên tin cậy hơn.
5.2. Sử dụng hồi quy bình phương tổng quát khả dĩ (FGLS)
Khi hiện tượng phương sai của sai số thay đổi quá nghiêm trọng, có thể dùng phương pháp Feasible Generalized Least Squares (FGLS). Phương pháp này điều chỉnh mô hình để xử lý đồng thời cả phương sai thay đổi và tự tương quan, giúp nâng cao hiệu quả ước lượng. Tuy nhiên, cần thận trọng vì FGLS yêu cầu giả định về cấu trúc của sai số.
6. Kết luận
Hiện tượng phương sai của sai số thay đổi là một vấn đề thường gặp trong hồi quy tuyến tính và có thể làm sai lệch các kết luận nếu không được phát hiện và xử lý đúng cách. Việc áp dụng kiểm định White, kiểm định Breusch–Pagan, cùng với các biện pháp như robust standard errors hoặc FGLS sẽ giúp mô hình đáng tin cậy hơn.
Hy vọng hướng dẫn từ Xử lý số liệu giúp bạn hiểu rõ heteroskedasticity là gì, nắm được cách phát hiện phương sai thay đổi và khắc phục phương sai thay đổi trong Stata. Việc xử lý đúng phương sai của sai số thay đổi không chỉ giúp mô hình chính xác hơn mà còn củng cố độ tin cậy cho toàn bộ nghiên cứu.
Hệ số chặn là gì? Ý nghĩa của hệ số chặn (Intercept) trong mô hình hồi quy tuyến tính
Trong phân tích hồi quy, việc hiểu rõ hệ số chặn là gì là bước quan trọng để diễn giải đúng mô hình. Hệ số chặn hay còn gọi là intercept thể hiện giá trị trung bình của biến phụ thuộc khi tất cả các biến độc lập bằng 0. Bài viết dưới đây của Xử lý số liệu sẽ giúp bạn hiểu sâu hơn về khái niệm, ý nghĩa và cách tính hệ số chặn trong mô hình hồi quy tuyến tính, kèm theo các ví dụ cụ thể trên SPSS.
1. Hệ số chặn là gì trong phương trình hồi quy?
Hệ số chặn là gì? Trong mô hình hồi quy tuyến tính, hệ số chặn (ký hiệu là b0) là giá trị cố định thể hiện điểm xuất phát của mô hình. Nó cho biết giá trị dự đoán của biến phụ thuộc Y khi tất cả các biến độc lập X đều bằng 0.
Phương trình tổng quát của hồi quy tuyến tính đơn:
Y = b0 + b1X
Trong đó:
- Y: Biến phụ thuộc (Dependent Variable)
- X: Biến độc lập (Independent Variable)
- b1: Hệ số hồi quy của biến X
- b0: Hệ số chặn (Intercept)
Hiểu đơn giản, hệ số chặn là gì – đó là giá trị Y dự đoán khi X = 0. Trong nhiều mô hình, nó còn được xem là điểm cắt giữa đường hồi quy và trục tung.
Ký hiệu của hệ số chặn trong hồi quy
Ví dụ phương trình hồi quy: Y = 1 + 0.5X
Ở đây, hệ số chặn b0 = 1. Nghĩa là khi X = 0, giá trị dự đoán của Y sẽ bằng 1. Đây là ví dụ cơ bản giúp bạn hình dung dễ dàng hơn khi học intercept trong hồi quy.
2. Ví dụ về hệ số chặn trong mô hình hồi quy
Giả sử ta muốn phân tích nhu cầu vay vốn của 20 xưởng gia công quần áo dựa trên quy mô sản xuất và lãi suất ngân hàng. Mô hình hồi quy thu được như sau:
I = 26,11 + 32,5Q – 2,65R
Trong đó:
- I: Nhu cầu vay vốn của xưởng (tỷ đồng)
- Q: Sản lượng dự kiến (nghìn bộ/năm)
- R: Lãi suất cho vay (%)
Ở mô hình này, hệ số chặn b0 = 26,11. Điều này có nghĩa là nếu Q = 0 và R = 0, nhu cầu vay vốn sẽ là 26,11 tỷ đồng.
Dù giá trị này ít khi có ý nghĩa thực tế (vì không tồn tại trường hợp lãi suất = 0), nhưng nó vẫn là phần quan trọng trong phương trình. Hiểu được ý nghĩa hệ số chặn trong mô hình giúp ta nắm rõ cấu trúc của mô hình và khả năng dự đoán của các biến.
3. Ý nghĩa của hệ số chặn trong mô hình hồi quy
Khi phân tích kết quả hồi quy trên SPSS, bạn thường thấy dòng “Constant” trong bảng Coefficients. Đây chính là diễn giải hệ số chặn trong SPSS.
Ví dụ, ta có kết quả hồi quy như sau:
- Biến phụ thuộc: HAILONG (Sự hài lòng của khách hàng)
- Các biến độc lập: TINCAY, DAPUNG, DAMBAO, CAMTHONG, HUUHINH, MINHBACH
- Hệ số chặn (Constant) = -0.938
Vì các biến này được đo theo thang Likert 1-5, nên khi tất cả các biến độc lập bằng 0 là điều không thể xảy ra trong thực tế. Do đó, hệ số chặn trong trường hợp này không mang ý nghĩa quản trị thực tế mà chỉ có vai trò kỹ thuật trong mô hình hồi quy.
Nói cách khác, ý nghĩa hệ số chặn trong mô hình là thể hiện giá trị cơ sở của biến phụ thuộc khi các yếu tố tác động chưa xuất hiện. Trong một số nghiên cứu, nếu giá trị hệ số chặn âm hoặc dương nhưng nằm ngoài phạm vi dữ liệu, ta có thể bỏ qua việc diễn giải nó.
4. Cách tính hệ số chặn trong hồi quy
Cách tính hệ số chặn dựa vào công thức của hồi quy tuyến tính đơn:
b0 = Ȳ – b1X̄
Trong đó:
- Ȳ: Giá trị trung bình của biến phụ thuộc
- X̄: Giá trị trung bình của biến độc lập
- b1: Hệ số hồi quy của X
Nhờ công thức này, bạn có thể tính toán thủ công hệ số chặn khi biết các giá trị trung bình và hệ số hồi quy. Trong phần mềm SPSS, giá trị này được tính tự động khi bạn chạy lệnh hồi quy, hiển thị trong phần “Coefficients – Constant”.
5. Diễn giải hệ số chặn trong SPSS
Khi làm việc trên SPSS, để hiểu đúng diễn giải hệ số chặn trong SPSS, bạn cần đối chiếu giá trị Constant với bản chất của dữ liệu.
- Nếu dữ liệu có giá trị 0 là hợp lý (ví dụ X là số năm kinh nghiệm), thì hệ số chặn có thể được diễn giải thực tế.
- Nếu dữ liệu không có giá trị 0 (ví dụ thang Likert 1–5), thì hệ số chặn chỉ có vai trò kỹ thuật.
Điều quan trọng là nhận ra rằng hệ số chặn là gì không chỉ là một con số, mà là phần khởi điểm của đường hồi quy – nơi mọi tác động bắt đầu.
6. Tổng kết về hệ số chặn
Qua bài viết này, bạn đã hiểu rõ hệ số chặn là gì, ý nghĩa hệ số chặn trong mô hình và cách tính hệ số chặn trong phân tích hồi quy tuyến tính. Mặc dù đôi khi giá trị hệ số chặn không mang ý nghĩa thực tế, nhưng nó vẫn là thành phần quan trọng để xác định hình dạng và vị trí của đường hồi quy.
Để thực hành thêm về intercept trong hồi quy hoặc chạy hồi quy trong SPSS, bạn có thể tham khảo các hướng dẫn chi tiết tại xulysolieu.info. Trang cung cấp các bài viết chuyên sâu về phân tích dữ liệu, ví dụ hệ số chặn, và nhiều công cụ hỗ trợ người học SPSS từ cơ bản đến nâng cao.