Coefficient là gì? Trong thống kê, thuật ngữ coefficient (hệ số) được dùng để biểu thị mức độ và hướng của mối quan hệ giữa hai hay nhiều biến. Một trong những hệ số quan trọng nhất là hệ số tương quan – tiếng Anh là Correlation Coefficient – được sử dụng phổ biến trong nhiều lĩnh vực như kinh tế, tài chính, và khoa học dữ liệu.
Mục lục
Toggle1. Hệ số tương quan là gì?
Hệ số tương quan là chỉ số thống kê đo lường mức độ mạnh yếu và chiều hướng của mối quan hệ giữa hai biến định lượng. Giá trị của hệ số này dao động trong khoảng từ -1 đến 1:
| Giá trị hệ số | Ý nghĩa |
|---|---|
| -1 | Tương quan âm tuyệt đối (nghịch biến hoàn toàn) |
| 0 | Không có mối tương quan (hai biến độc lập nhau) |
| 1 | Tương quan dương tuyệt đối (đồng biến hoàn toàn) |
Hiểu đơn giản, khi một biến tăng mà biến kia cũng tăng, ta có tương quan dương. Ngược lại, nếu một biến tăng còn biến kia giảm, đó là tương quan âm. Còn khi hai biến không có mối liên hệ nào, hệ số tương quan bằng 0.
2. Cách tính hệ số tương quan Pearson
Trong thống kê, có nhiều loại hệ số tương quan khác nhau (như Spearman, Kendall…), tuy nhiên phổ biến nhất là hệ số tương quan Pearson. Đây là chỉ số đo lường mối quan hệ tuyến tính giữa hai biến số.
Công thức tính hệ số tương quan Pearson như sau:
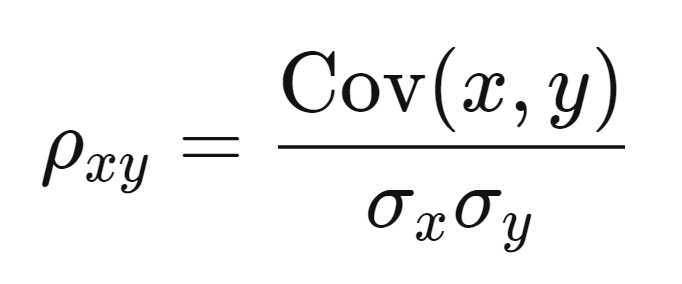
Trong đó:
- ρxy: Hệ số tương quan Pearson
- Cov(x, y): Hiệp phương sai giữa hai biến x và y
- σx, σy: Độ lệch chuẩn của x và y
Độ lệch chuẩn thể hiện mức độ phân tán của dữ liệu, trong khi hiệp phương sai thể hiện xu hướng đồng biến hoặc nghịch biến giữa hai biến.
3. Ý nghĩa và cách diễn giải hệ số tương quan
Giá trị của hệ số tương quan phản ánh mức độ mạnh yếu của mối quan hệ giữa hai biến. Bảng sau minh họa cách diễn giải thông thường:
| Giá trị |ρxy| | Mức độ tương quan |
|---|---|
| 0.0 – 0.2 | Rất yếu hoặc gần như không có |
| 0.2 – 0.4 | Yếu |
| 0.4 – 0.6 | Trung bình |
| 0.6 – 0.8 | Mạnh |
| 0.8 – 1.0 | Rất mạnh |
Lưu ý: Pearson chỉ đo lường mối quan hệ tuyến tính. Nếu hai biến có mối quan hệ phi tuyến (chẳng hạn như dạng parabol), hệ số tương quan có thể bằng 0 dù chúng vẫn có mối liên hệ nhất định.
4. Ứng dụng của hệ số tương quan trong tài chính

Trong lĩnh vực tài chính và đầu tư, hệ số tương quan là công cụ quan trọng giúp đánh giá mối quan hệ giữa các tài sản, chỉ số hoặc danh mục đầu tư. Dưới đây là một số ví dụ cụ thể:
Ví dụ 1: Mối tương quan giữa giá dầu và cổ phiếu công ty dầu khí
Nếu ta tính được hệ số tương quan dương giữa giá dầu thô và cổ phiếu của công ty Exxon Mobil, điều đó cho thấy khi giá dầu tăng thì giá cổ phiếu cũng có xu hướng tăng. Đây là mối tương quan đồng biến dương – phản ánh tác động trực tiếp của thị trường hàng hóa lên doanh nghiệp.
Ví dụ 2: Đa dạng hóa danh mục đầu tư
Nhà đầu tư có thể kết hợp các tài sản có hệ số tương quan thấp hoặc âm trong cùng một danh mục để giảm thiểu rủi ro. Khi một tài sản giảm giá, tài sản khác có thể tăng, giúp ổn định tổng thể danh mục.
Ví dụ 3: Phân tích mối tương quan với lãi suất
Giá cổ phiếu của ngân hàng thường có tương quan dương với lãi suất thị trường. Nếu lãi suất tăng mà cổ phiếu ngân hàng lại giảm, điều này có thể phản ánh vấn đề nội tại của ngân hàng chứ không phải do yếu tố thị trường.
5. Kết luận
Qua bài viết trên, bạn đã hiểu rõ hơn về coefficient là gì – đặc biệt là hệ số tương quan (correlation coefficient). Đây là công cụ cực kỳ hữu ích để phân tích mối quan hệ giữa các biến trong nghiên cứu thống kê, tài chính và dữ liệu. Việc nắm vững cách tính và diễn giải hệ số này giúp bạn đưa ra quyết định đầu tư và dự đoán xu hướng thị trường chính xác hơn.
Hy vọng rằng bài viết đã giúp bạn hiểu rõ hơn về khái niệm hệ số tương quan – một nền tảng quan trọng trong phân tích tài chính hiện đại.