Sau bước đánh giá mô hình đo lường trên SmartPLS 4, chúng ta sẽ tiếp tục thực hiện đánh giá mô hình cấu trúc. Trong nghiên cứu định lượng, việc đánh giá mô hình cấu trúc đóng vai trò quan trọng trong việc xác định mối quan hệ giữa các biến.
SmartPLS 4 là công cụ mạnh mẽ giúp thực hiện phân tích mô hình cấu trúc dựa trên phương pháp PLS-SEM, đặc biệt hiệu quả với các mô hình phức tạp. Bài viết này sẽ cung cấp hướng dẫn chi tiết về cách đánh giá các yếu tố quan trọng như hiện tượng cộng tuyến, hệ số R bình phương và hệ số f bình phương, nhằm giúp bạn nắm bắt rõ ràng hơn về phương pháp phân tích này.
Ở đây tiếp tục sử dùng mô hình nghiên cứu trong bước đánh giá mô hình đo lường trên SmartPLS 4 như sau:
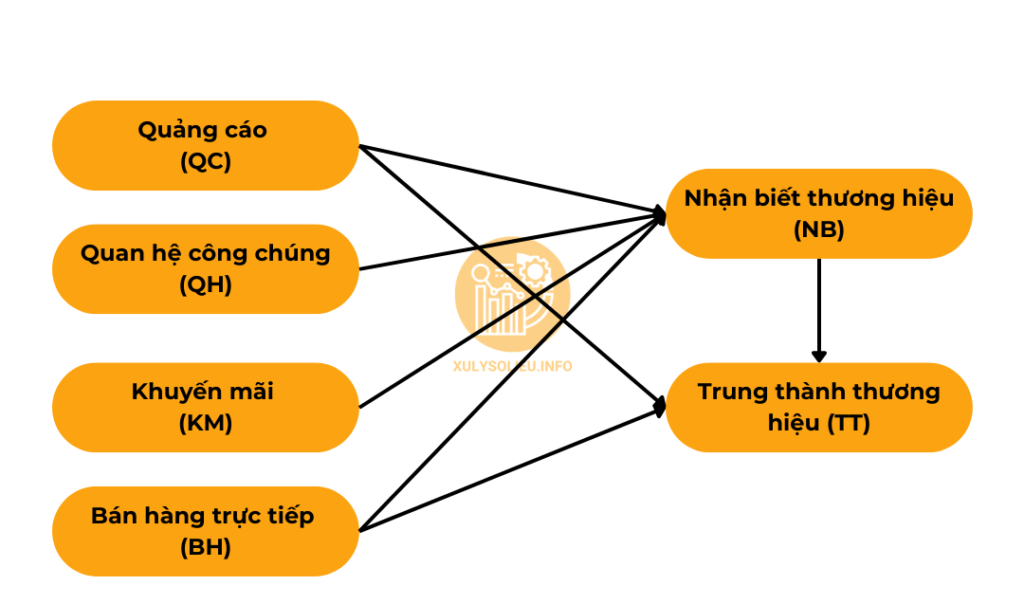
Mô hình cấu trúc trên SmartPLS 4
Mục lục
ToggleHiện tượng cộng tuyến của các biến độc lập trong mô hình cấu trúc
Khi đánh giá mô hình cấu trúc, bước quan trọng đầu tiên là nhận diện các biến độc lập trong mô hình. Việc hiểu rõ khái niệm “biến độc lập” trong từng bối cảnh cụ thể là cần thiết, bởi một biến có thể đóng vai trò độc lập trong một mô hình, nhưng lại là biến phụ thuộc trong mô hình khác. Ví dụ, biến NB có thể được coi là biến độc lập khi xét tác động của nó đến TT, nhưng trong mô hình khác, nó có thể đóng vai trò là biến phụ thuộc khi bị tác động bởi các biến khác như QC, QH, KM và BH.
Trong mô hình cấu trúc, hiện tượng cộng tuyến xảy ra khi có sự tương quan quá lớn giữa hai hoặc nhiều biến độc lập cùng tác động lên một biến phụ thuộc. Đối với các mô hình đơn trong ví dụ, có hai nhóm biến độc lập cần xem xét hiện tượng cộng tuyến:
– Nhóm biến độc lập của NB bao gồm QC, QH, KM và BH.
– Nhóm biến độc lập của TT bao gồm QC, BH và NB.
Nếu hiện tượng cộng tuyến xuất hiện, kết quả ước lượng trong phân tích đường dẫn sẽ bị sai lệch, ảnh hưởng đến tính chính xác của các hệ số tác động. Hệ số tác động có thể biến đổi từ dương sang âm, hoặc từ có ý nghĩa thống kê trở thành không có ý nghĩa. Do đó, việc phát hiện và xử lý hiện tượng cộng tuyến là cần thiết để đảm bảo độ tin cậy của kết quả phân tích.
Để đánh giá hiện tượng cộng tuyến, hệ số VIF (variance inflation factor) thường được sử dụng. Hair và cộng sự (2019) đã đưa ra các ngưỡng giá trị VIF như sau:
– VIF ≥ 5: Có khả năng rất cao xảy ra hiện tượng cộng tuyến, mô hình bị ảnh hưởng nghiêm trọng.
– 3 ≤ VIF < 5: Mô hình có khả năng xảy ra cộng tuyến.
– VIF < 3: Mô hình không gặp phải hiện tượng cộng tuyến.
Trong SMARTPLS 4, để kiểm tra hệ số VIF của các biến độc lập trên SMARTPLS 4, bạn cần truy cập kết quả phân tích PLS-SEM algorithm, sau đó chọn “Collinearity statistics (VIF)” và tiếp tục chọn “Inner model – List“. Nếu giá trị VIF vượt quá ngưỡng cho phép, biến độc lập có thể bị loại bỏ để cải thiện độ chính xác của mô hình.
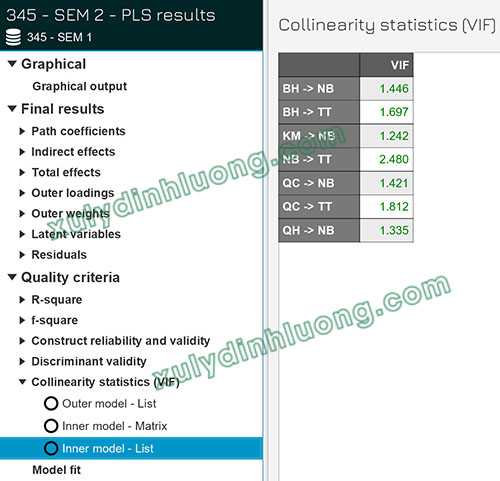
Ý nghĩa các mối quan hệ tác động trong mô hình cấu trúc
Một trong những yếu tố quan trọng trong việc đánh giá mô hình cấu trúc là kiểm định ý nghĩa thống kê của các mối quan hệ trong mô hình. Việc xem xét các mối quan hệ này bao gồm cả tác động trực tiếp và tác động điều tiết.
Để xác định các mối quan hệ có ý nghĩa thống kê hay không, chúng ta dựa trên kết quả phân tích hệ số đường dẫn (Path coefficients). Khi phân tích kết quả, cần chú trọng hai yếu tố chính: mối quan hệ đó có ý nghĩa thống kê không và chiều cũng như độ lớn của hệ số tác động (âm hay dương).
Đánh giá ý nghĩa thống kê của mối quan hệ tác động
Để đánh giá liệu một mối quan hệ trong mô hình có ý nghĩa thống kê hay không, ta dựa vào giá trị kiểm định t hoặc p-value. Thông thường, p-value được sử dụng rộng rãi hơn do tính tiện lợi và dễ dàng so sánh.
Mức ý nghĩa thường được đặt là 0,05 và cũng là mức mặc định trong SMARTPLS 4. Nếu p-value nhỏ hơn 0,05, mối quan hệ đó được coi là có ý nghĩa thống kê. Ngược lại, nếu p-value lớn hơn 0,05, tác động này không có ý nghĩa thống kê. Tuy nhiên, trong trường hợp này, các biến vẫn được giữ lại trong mô hình để phân tích tiếp, chứ không bị loại bỏ.
Đánh giá mức độ và chiều tác động
Thuật toán trên SMARTPLS 4 tự động xuất ra hệ số tác động chuẩn hóa, nằm trong khoảng từ -1 đến +1. Hệ số dương (+) biểu thị mối quan hệ tác động thuận chiều, còn hệ số âm (-) biểu thị mối quan hệ nghịch chiều.
Nếu hệ số tiến gần +1 hoặc -1, điều đó cho thấy mối quan hệ có tác động mạnh. Hệ số càng gần 0, mối quan hệ càng yếu.
Để so sánh mức độ tác động giữa các biến độc lập lên một biến phụ thuộc, ta sử dụng trị tuyệt đối của hệ số tác động chuẩn hóa. Biến nào có trị tuyệt đối lớn hơn sẽ có tác động mạnh hơn. Kết quả phân tích hệ số đường dẫn từ Bootstrapping giúp chúng ta đánh giá và đưa ra những kết luận cụ thể về các mối quan hệ này.
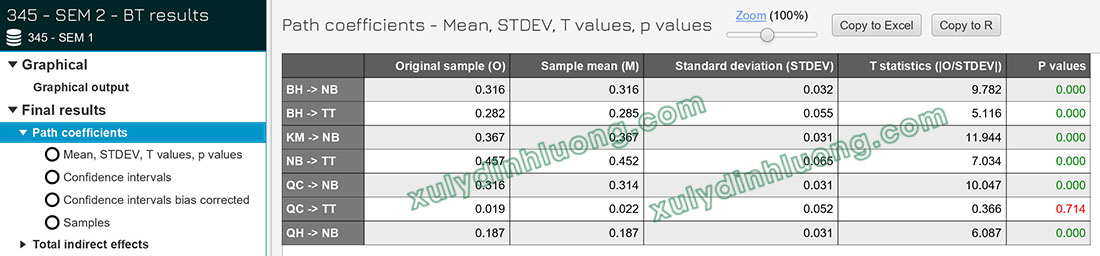
Khi đọc kết quả, ta tập trung vào hai cột chính:
1. Original sample: Hệ số tác động chuẩn hóa của mẫu gốc.
2. P values: Mức ý nghĩa của kiểm định t.
Ngoài ra, chúng ta còn có thể xem xét thêm các chỉ số khác như:
– Sample mean: Hệ số tác động chuẩn hóa trung bình từ tất cả các mẫu Bootstrapping.
– Standard deviation: Độ lệch chuẩn của hệ số tác động chuẩn hóa.
Ví dụ, trong một mô hình phân tích, nếu giá trị p-value từ QC lên TT là 0,714 (lớn hơn 0,05), điều này cho thấy mối quan hệ này không có ý nghĩa thống kê. Tuy nhiên, các mối quan hệ khác có p-value nhỏ hơn 0,05 đều có ý nghĩa thống kê. Toàn bộ hệ số tác động trong ví dụ này đều là dương, tức là tất cả mối quan hệ đều tác động thuận chiều.
Sau khi đánh giá thứ tự tác động, kết quả cho thấy các biến có tác động mạnh đến NB lần lượt là: KM (0,367) > QC (0,316) > BH (0,316) > QH (0,187). Tương tự, đối với TT, thứ tự tác động từ mạnh đến yếu là: NB (0,457) > BH (0,282).
Hệ số xác định R bình phương (R square)
Hệ số R bình phương biểu thị mức độ giải thích của một hoặc nhiều biến độc lập đối với biến phụ thuộc. Trong các mô hình cấu trúc, giá trị R bình phương tiến gần đến 1 cho thấy các biến độc lập giải thích tốt sự biến thiên của biến phụ thuộc, trong khi giá trị gần 0 chỉ ra mức độ giải thích thấp. Bên cạnh đó, chỉ số R bình phương điều chỉnh (R-square adjusted) cung cấp một bức tranh chính xác hơn về mức độ giải thích khi có nhiều biến độc lập tham gia vào mô hình.

Hệ số tác động f bình phương (f square)
Hệ số f bình phương giúp đánh giá mức độ quan trọng của một biến độc lập đối với biến phụ thuộc. Các ngưỡng đánh giá được gợi ý bởi Cohen (1988) như sau:
– f square < 0.02: Tác động rất nhỏ hoặc không có tác động.
– 0.02 ≤ f square < 0.15: Tác động nhỏ.
– 0.15 ≤ f square < 0.35: Tác động trung bình.
– f square ≥ 0.35: Tác động lớn.
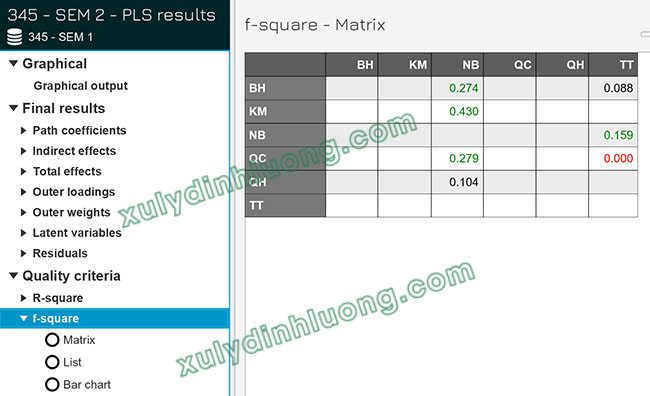
Trong SMARTPLS 4, việc đánh giá hệ số f bình phương có thể được thực hiện qua mục “f-square”. Kết quả sẽ giúp xác định biến nào có tác động mạnh nhất đến biến phụ thuộc, từ đó hỗ trợ việc tối ưu hóa mô hình nghiên cứu.
Tóm lại, việc đánh giá hiện tượng cộng tuyến, ý nghĩa của các quan hệ tác động, và các hệ số như R bình phương và f bình phương trong mô hình cấu trúc là những bước quan trọng trong phân tích PLS-SEM, nhằm đảm bảo tính chính xác và hiệu lực của mô hình nghiên cứu.
Nhận trợ giúp cho phân tích SMARTPLS của bạn

Dịch vụ chạy SmartPLS giá rẻ cho sinh viên
Nếu bạn gặp khó khăn trong việc chạy dữ liệu trên SmartPLS 4, hãy bắt đầu hành trình nghiên cứu với xulysolieu.info, nơi đội ngũ tận tâm của chúng tôi cung cấp hỗ trợ phân tích dữ liệu chuyên môn cho sinh viên, học giả và cá nhân. Chúng tôi đảm bảo nghiên cứu của bạn được nâng cao với độ chính xác. Khám phá các trang của chúng tôi:
Dùng chỉ số HTMT để đánh giá tính phân biệt của thang đo trong SmartPLS 4
Giá trị hệ số tải ngoài Outer Loading trong SmartPLS 4
Biểu đồ Tầm quan trọng hiệu suất IPMA trong SmartPLS 4
Hoặc bạn có thể trực tiếp liên hệ thông quan fanpage chính thức và Dịch vụ Smart PLS trên trang web chính thức của xulysolieu.info.















