Trong phân tích mô hình cấu trúc (SEM), việc đảm bảo tính phân biệt giữa các biến tiềm ẩn là một yếu tố quan trọng để xác định độ tin cậy và tính hợp lý của mô hình. Một trong những phương pháp phổ biến để đánh giá giá trị phân biệt là thông qua bảng Fornell and Larcker.
Được đề xuất bởi Fornell và Larcker vào năm 1981, phương pháp này giúp kiểm tra mức độ phân biệt giữa các biến tiềm ẩn bằng cách so sánh căn bậc hai của giá trị AVE với các tương quan giữa các biến tiềm ẩn khác. Việc đảm bảo giá trị phân biệt không chỉ giúp tránh tình trạng biến bị trùng lắp mà còn nâng cao chất lượng của các mô hình đo lường và cấu trúc trong nghiên cứu.
Mục lục
Toggle1. Lý thuyết về bảng Fornell và Larcker
Phương pháp Fornell và Larcker (1981) được sử dụng để đánh giá tính phân biệt của thang đo trong mô hình SEM (Structural Equation Modeling). Phương pháp này so sánh căn bậc hai của phương sai trích (AVE) (SQRT(AVE)) của mỗi biến tiềm ẩn với hệ số tương quan giữa biến tiềm ẩn đó với các biến tiềm ẩn khác. Trong đó, chỉ số AVE (Average Variance Extracted) là mức độ mà biến nghiên cứu giải thích sự biến thiên của các biến quan sát nó. Khi hệ số SQRT(AVE) vượt trội so với các hệ số tương quan còn lại, thang đo được xem là đạt yêu cầu.
2. Đánh giá tính phân biệt bằng bảng Fornell và Larcker
Giả sử chúng ta có mô hình SEM với 3 biến tiềm ẩn: X, Y và Z. Bảng Fornell và Larcker cho mô hình này là ma trận tương quan giữa ba biến tiềm ẩn X, Y và Z và chỉ số AVE, như sau:
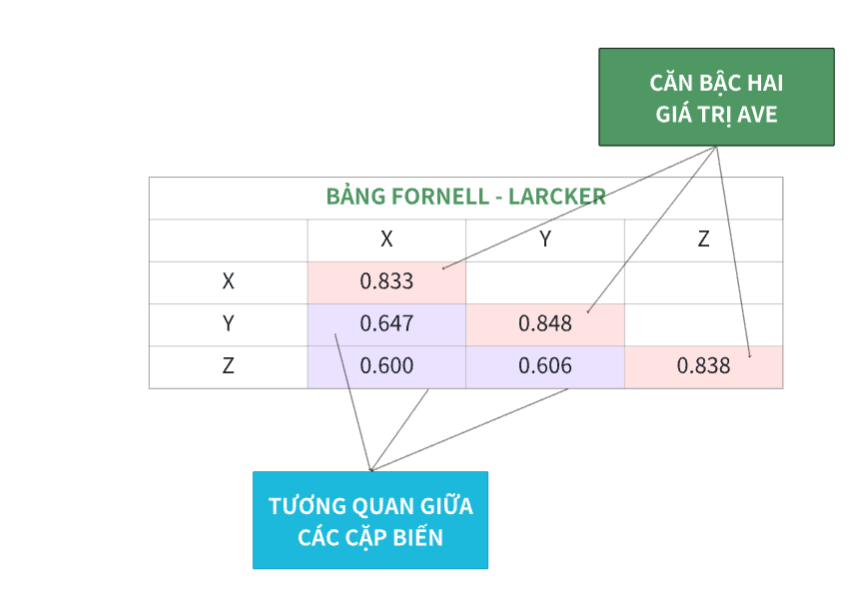
Bảng Fornell và Larcker
Bảng Fornell và Larcker cung cấp cho thấy:
- X: Giá trị căn bậc hai của AVE là 0.833.
- Y: Giá trị căn bậc hai của AVE là 0.848.
- Z: Giá trị căn bậc hai của AVE là 0.838.
Các giá trị này đều lớn hơn so với các giá trị tương quan giữa các hạng mục, cho thấy tính hợp lệ phân biệt giữa các hạng mục trong mô hình đo lường:
- X và Y: Tương quan là 0.647.
- X và Z: Tương quan là 0.600.
- Y và Z: Tương quan là 0.606.
Điều này chứng minh rằng mỗi hạng mục có tính độc lập cao so với các hạng mục khác, đáp ứng tiêu chuẩn Fornell và Larcker trong việc kiểm định tính hợp lệ của mô hình đo lường.
Cách đọc bảng Fornell và Larcker
Bảng Fornell và Larcker hoạt động bằng cách so sánh giá trị SQRT(AVE) với hệ số tương quan giữa các biến tiềm ẩn. Nếu giá trị SQRT(AVE) cao hơn tất cả các hệ số tương quan, thang đo được xem là đạt được tính phân biệt. Việc sử dụng bảng Fornell và Larcker mang lại nhiều lợi ích, bao gồm giúp xác định những điểm yếu trong thang đo, cải thiện tính phân biệt của thang đo, tăng cường độ tin cậy và hiệu lực của mô hình SEM.
Trong phần dưới đây, chúng ta sẽ cùng tìm hiểu chi tiết cách đọc và hiểu bảng Fornell và Larcker.
Xác định các thành phần của bảng:
– Hàng và cột đầu tiên: Liệt kê các biến tiềm ẩn trong mô hình.
– Hàng và cột thứ hai: Hiển thị giá trị SQRT(AVE) của mỗi biến tiềm ẩn.
– Các ô còn lại: Hiển thị hệ số tương quan giữa từng cặp biến tiềm ẩn.
Phân tích giá trị SQRT(AVE):
So sánh giá trị SQRT(AVE) của mỗi biến tiềm ẩn với tất cả các hệ số tương quan trong cùng cột.
– Nếu giá trị SQRT(AVE) cao hơn tất cả các hệ số tương quan trong cùng cột: Biến tiềm ẩn đó đạt được tính phân biệt.
– Nếu giá trị SQRT(AVE) thấp hơn một hoặc nhiều hệ số tương quan trong cùng cột: Biến tiềm ẩn đó có thể không đạt được tính phân biệt.
Phân tích hệ số tương quan:
So sánh giá trị tuyệt đối của hệ số tương quan giữa hai biến tiềm ẩn với giá trị SQRT(AVE) của cả hai biến tiềm ẩn đó.
– Nếu giá trị tuyệt đối của hệ số tương quan thấp hơn giá trị SQRT(AVE) của cả hai biến tiềm ẩn: Hai biến tiềm ẩn đó đạt được tính phân biệt.
– Nếu giá trị tuyệt đối của hệ số tương quan cao hơn giá trị SQRT(AVE) của một hoặc cả hai biến tiềm ẩn: Hai biến tiềm ẩn đó có thể không đạt được tính phân biệt.

Giao diện bảng Fornell-Larcker trên SMARTPLS 4
Bảng Fornell và Larcker chỉ là một trong nhiều phương pháp để đánh giá tính phân biệt của thang đo, cần sử dụng nhiều phương pháp khác nhau để đánh giá tính tin cậy và hiệu lực của mô hình SEM.
Nhận trợ giúp cho phân tích SMARTPLS của bạn

Dịch vụ chạy SmartPLS giá rẻ cho sinh viên
Nếu bạn gặp khó khăn trong việc chạy dữ liệu trên SmartPLS 4, hãy bắt đầu hành trình nghiên cứu với xulysolieu.info, nơi đội ngũ tận tâm của chúng tôi cung cấp hỗ trợ phân tích dữ liệu chuyên môn cho sinh viên, học giả và cá nhân. Chúng tôi đảm bảo nghiên cứu của bạn được nâng cao với độ chính xác. Khám phá các trang của chúng tôi:
Dùng chỉ số HTMT để đánh giá tính phân biệt của thang đo trong SmartPLS 4
Giá trị hệ số tải ngoài Outer Loading trong SmartPLS 4
Biểu đồ Tầm quan trọng hiệu suất IPMA trong SmartPLS 4
Hoặc bạn có thể trực tiếp liên hệ thông quan fanpage chính thức và Dịch vụ Smart PLS trên trang web chính thức của xulysolieu.info.
/
5
(
2
votes
)















