Trong phân tích dữ liệu, việc xác định mối quan hệ giữa các biến là một bước quan trọng trước khi đi sâu vào mô hình hồi quy hay các kiểm định phức tạp hơn. Một trong những công cụ được sử dụng phổ biến nhất cho mục tiêu này chính là hệ số tương quan pearson. Với ưu điểm dễ tính, dễ đọc kết quả và được tích hợp sẵn trong SPSS, phương pháp này đặc biệt phù hợp khi làm việc với dữ liệu định lượng.

Bài viết dưới đây sẽ giúp bạn hiểu rõ hệ số tương quan pearson là gì, công thức tính, cách thực hiện trong SPSS và quan trọng nhất là cách diễn giải kết quả một cách đúng đắn trong nghiên cứu và thực tiễn phân tích số liệu.

1. Hệ số tương quan Pearson là gì?

Hệ số tương quan pearson (pearson correlation) là một chỉ số thống kê dùng để đo lường mức độ và chiều hướng mối quan hệ tuyến tính giữa hai biến định lượng. Nói cách khác, nó cho biết khi một biến thay đổi thì biến còn lại có xu hướng thay đổi như thế nào.

Trong phân tích mối quan hệ, hệ số tương quan pearson thường được dùng để trả lời các câu hỏi như:

• Thu nhập có liên quan đến mức chi tiêu hay không?
• Thời gian học tập có ảnh hưởng đến kết quả thi không?
• Áp lực công việc và hiệu suất làm việc có mối liên hệ nào không?

Nhờ khả năng phản ánh cả mức độ mạnh – yếu và hướng của mối quan hệ, hệ số tương quan pearson được xem là nền tảng trong thống kê mô tả và phân tích dữ liệu ban đầu.

2. Điều kiện áp dụng hệ số tương quan Pearson

Để sử dụng hệ số tương quan pearson một cách chính xác, bạn cần lưu ý một số điều kiện cơ bản:

• Cả hai biến đều là dữ liệu định lượng (thang đo khoảng hoặc tỷ lệ).
• Mối quan hệ giữa hai biến có xu hướng tuyến tính.
• Dữ liệu không có quá nhiều ngoại lệ nghiêm trọng.
• Phân phối dữ liệu không quá lệch (trong thực tế có thể linh hoạt).

Nếu các điều kiện này không được đáp ứng, kết quả pearson correlation có thể gây hiểu nhầm và bạn nên cân nhắc các phương pháp khác.

3. Công thức tính hệ số tương quan Pearson

Về mặt lý thuyết, hệ số tương quan pearson được tính theo công thức:

r = [NΣxy − (Σx)(Σy)] / √{[NΣx² − (Σx)²][NΣy² − (Σy)²]}

Trong đó:

• N: số cặp quan sát
• Σxy: tổng tích của các cặp giá trị x và y
• Σx, Σy: tổng giá trị của từng biến
• Σx², Σy²: tổng bình phương của từng biến

Trong thực tế nghiên cứu, bạn hiếm khi phải tính tay công thức này. Tuy nhiên, việc hiểu công thức giúp bạn nắm rõ bản chất của hệ số tương quan pearson, thay vì chỉ đọc một con số từ phần mềm.

4. Ý nghĩa của giá trị hệ số tương quan Pearson

Giá trị của hệ số tương quan pearson luôn nằm trong khoảng từ -1 đến +1. Mỗi khoảng giá trị mang một ý nghĩa khác nhau:

• r = 0: không tồn tại mối quan hệ tuyến tính
• r > 0: mối quan hệ thuận chiều
• r < 0: mối quan hệ nghịch chiều
• r = 1 hoặc r = -1: mối quan hệ tuyến tính hoàn hảo

Về mức độ mạnh – yếu của mối quan hệ, cách phân loại thường dùng trong phân tích mối quan hệ là:

• |r| ≥ 0,5: tương quan mạnh
• 0,3 ≤ |r| < 0,5: tương quan trung bình
• |r| < 0,3: tương quan yếu

Cần lưu ý rằng hệ số tương quan pearson chỉ phản ánh mối liên hệ tuyến tính, không khẳng định quan hệ nhân quả.

5. Phân tích hệ số tương quan Pearson trong SPSS

SPSS là công cụ được sử dụng rộng rãi để chạy spss correlation nhờ giao diện trực quan và kết quả rõ ràng. Các bước thực hiện như sau:

Bước 1: Thiết lập phân tích

Trên thanh menu, chọn Analyze → Correlate → Bivariate.

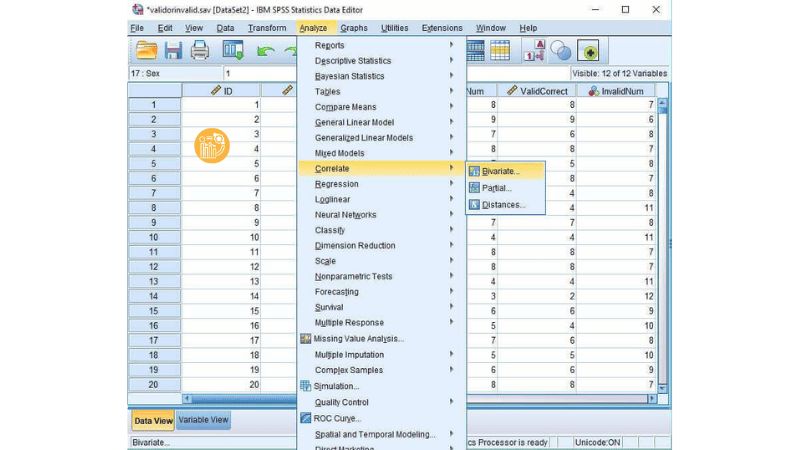
Bước 2: Chọn biến

Di chuyển hai biến định lượng cần phân tích sang ô Variables. Đảm bảo tùy chọn Pearson được tích chọn.

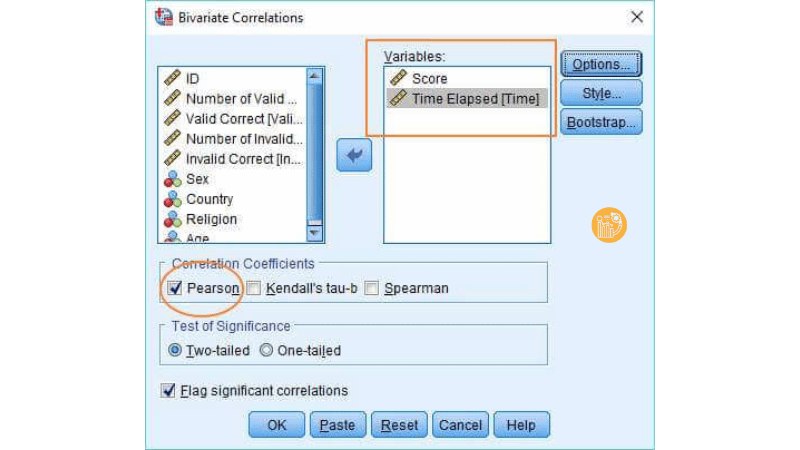
Bước 3: Thực hiện và xem kết quả

Nhấn OK để SPSS chạy phân tích và xuất bảng kết quả pearson correlation.

Trong bảng kết quả, bạn cần chú ý hai chỉ số chính: hệ số tương quan pearson (Pearson Correlation) và Sig. (p-value).

6. Cách đọc và diễn giải kết quả Pearson trong SPSS

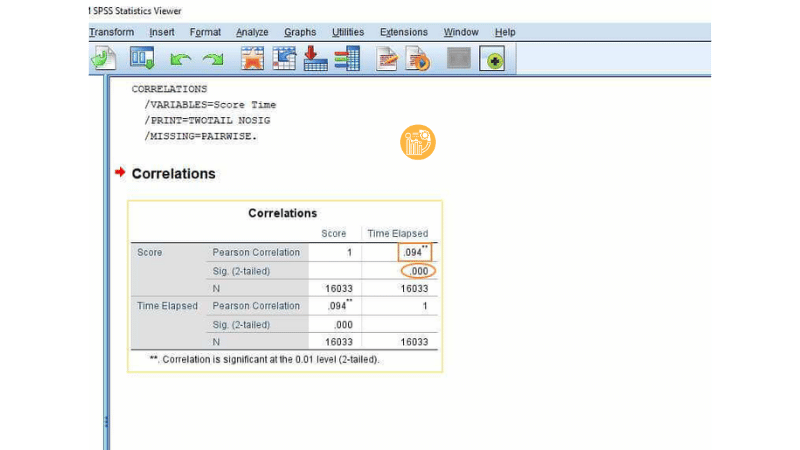
Khi phân tích kết quả thống kê từ SPSS, bạn nên đọc theo trình tự:

• Giá trị hệ số tương quan pearson để đánh giá mức độ và chiều hướng mối quan hệ.
• Giá trị Sig. để xác định mối quan hệ đó có ý nghĩa thống kê hay không.

Ví dụ: Pearson = 0,62 và Sig. = 0,001 cho thấy mối quan hệ thuận chiều, khá mạnh và có ý nghĩa thống kê. Điều này nghĩa là khi biến X tăng, biến Y có xu hướng tăng theo, và kết luận này đáng tin cậy về mặt thống kê.

Ngược lại, nếu Sig. > 0,05 thì dù hệ số tương quan pearson có lớn đến đâu, bạn cũng không nên kết luận có mối quan hệ rõ ràng.

7. Ví dụ minh họa phân tích mối quan hệ

Giả sử bạn nghiên cứu mối liên hệ giữa thời gian làm bài và điểm số đạt được. Cả hai đều là dữ liệu định lượng. Khi chạy spss correlation, bạn thu được hệ số tương quan pearson = 0,94 và Sig. < 0,01.

Kết quả này cho thấy tồn tại mối quan hệ thuận rất mạnh giữa thời gian và điểm số. Nói cách khác, người dành nhiều thời gian hơn có xu hướng đạt điểm cao hơn. Tuy nhiên, bạn vẫn cần kết hợp bối cảnh nghiên cứu để tránh diễn giải quá mức.

8. Những lưu ý quan trọng khi sử dụng hệ số tương quan Pearson

• Không dùng hệ số tương quan pearson cho dữ liệu định tính.
• Luôn kiểm tra ý nghĩa thống kê trước khi kết luận.
• Không đồng nhất tương quan với quan hệ nhân quả.
• Kết hợp với thống kê mô tả và đồ thị scatter để đánh giá trực quan.

Khi được sử dụng đúng cách, hệ số tương quan pearson là công cụ rất mạnh để khám phá dữ liệu và định hướng các phân tích tiếp theo.

9. Hỗ trợ xử lý số liệu và chạy SPSS

Nếu bạn gặp khó khăn trong việc lựa chọn phương pháp, chạy spss correlation hoặc diễn giải kết quả sao cho đúng chuẩn học thuật, bạn có thể tham khảo dịch vụ tại xulysolieu.info – Xử lý số liệu. Đội ngũ chuyên môn sẽ hỗ trợ từ thống kê mô tả, phân tích mối quan hệ đến viết diễn giải kết quả theo đúng yêu cầu nghiên cứu.

Liên hệ: 0878968468 hoặc truy cập xulysolieu.info để được tư vấn chi tiết.