Trang chủ » SPSS » Hướng dẫn phân tích thành phần chính Principal Component Analysis (PCA) – Phần 1

Hướng dẫn phân tích thành phần chính Principal Component Analysis (PCA) – Phần 1

Trong thế giới ngày nay, dữ liệu trở thành một trong những tài nguyên quý giá bậc nhất của các nhà nghiên cứu, nhà phát triển và doanh nghiệp. Đặc biệt trong lĩnh vực Machine Learning, pca hay còn gọi là phân tích thành phần chính đã trở thành một kỹ thuật không thể thiếu để xử lý các dữ liệu có đa chiều cao, giúp giảm chiều dữ liệu một cách tối ưu mà không làm mất đi quá nhiều thông tin quan trọng. Điểm đặc biệt của phương pháp này chính là khả năng tìm ra hệ cơ sở mới trong không gian dữ liệu, qua đó giúp các mô hình phân tích và dự đoán vận hành một cách trơn tru hơn.

Trong bài viết này, chúng ta sẽ đi làm rõ về các khái niệm nền tảng của pca, các bước thực hiện, cũng như các công cụ phổ biến hỗ trợ như Phân tích thành phần chính SPSS, phép phân rã giá trị riêng, hoặc biểu đồ Scree. Ngoài ra, bài viết còn phân tích chi tiết về cách xây dựng các ma trận tải trọng yếu tố, giảm chiều dữ liệu bằng các phần mềm như AMOS, nhằm giúp người đọc dễ hình dung và ứng dụng một cách rõ ràng và hiệu quả.

Mục lục

1. Giới thiệu

Dimensionality Reduction (Giảm chiều dữ liệu) là một trong những kỹ thuật quan trọng trong Machine Learning. Các feature vectors trong thực tế có thể có số chiều rất lớn (vài nghìn), dẫn đến khó khăn về lưu trữ và tốc độ tính toán. Giảm chiều giúp nén dữ liệu, tăng hiệu quả tính toán và loại bỏ nhiễu.

Một cách đơn giản, Dimensionality Reduction là việc tìm hàm:

x ∈ R^D → z ∈ R^K, với K < D

Trong bài này, ta sẽ tìm hiểu PCA (Principal Component Analysis) – phương pháp giảm chiều tuyến tính cơ bản và phổ biến nhất.

2. Một chút toán

2.1. Norm 2 của ma trận

||A||₂ = maxₓ (||A·x||₂ / ||x||₂)

Đặt điều kiện ||x||₂ = 1, ta có:

||A||₂ = max_||x||₂=1 ||A·x||₂

Giải bằng phương pháp Lagrange:

L(x, λ) = ||A·x||₂² + λ(1 - ||x||₂²)
⇒ AᵀA·x = λ·x

⇒ λ là trị riêng (eigenvalue) của AᵀA, và x là vector riêng (eigenvector) tương ứng.

Kết luận: Norm 2 của ma trận A chính là singular value lớn nhất của A.

2.2. Biểu diễn vector trong các hệ cơ sở khác nhau

x = y₁u₁ + y₂u₂ + ... + y_Du_D = U·y
⇒ y = U⁻¹x

Nếu U là ma trận trực giao, thì U⁻¹ = Uᵀ, do đó:

y = Uᵀx

→ Đây là cách chuyển hệ cơ sở (xoay trục toạ độ trong không gian vector).

Bieu-dien-vector-trong-cac-he-co-so-khac-nhau

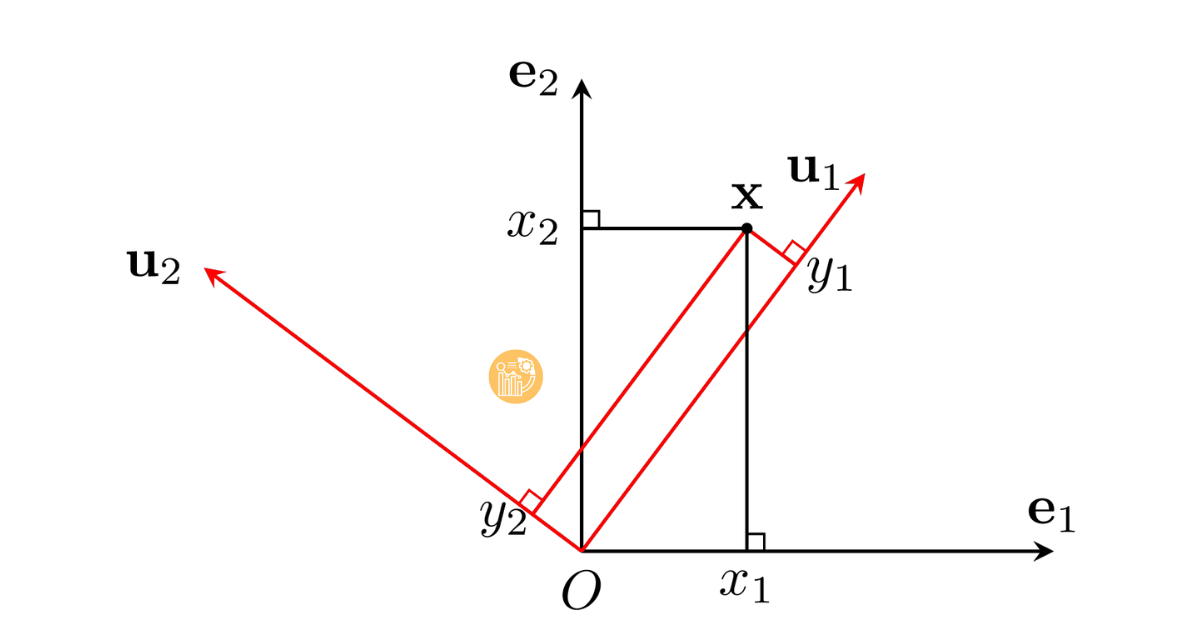
Hình 1: Chuyển đổi toạ độ trong các hệ cơ sở khác nhau.

2.3. Tính chất của Trace

trace(A) = trace(Aᵀ)
trace(AB) = trace(BA)
||A||_F² = trace(AᵀA) = trace(AAᵀ)
trace(A) = ∑λ_i (tổng các trị riêng)

2.4. Kỳ vọng và ma trận hiệp phương sai

a) Dữ liệu 1 chiều

x̄ = (1/N) ∑xᵢ
σ² = (1/N) ∑(xᵢ - x̄)²

b) Dữ liệu nhiều chiều

x̄ = (1/N) ∑xᵢ
S = (1/N) ∑(xᵢ - x̄)(xᵢ - x̄)ᵀ

Đặc điểm:

S là ma trận đối xứng và nửa xác định dương
Phần tử chéo: phương sai từng chiều
Phần tử ngoài chéo: hiệp phương sai giữa các chiều

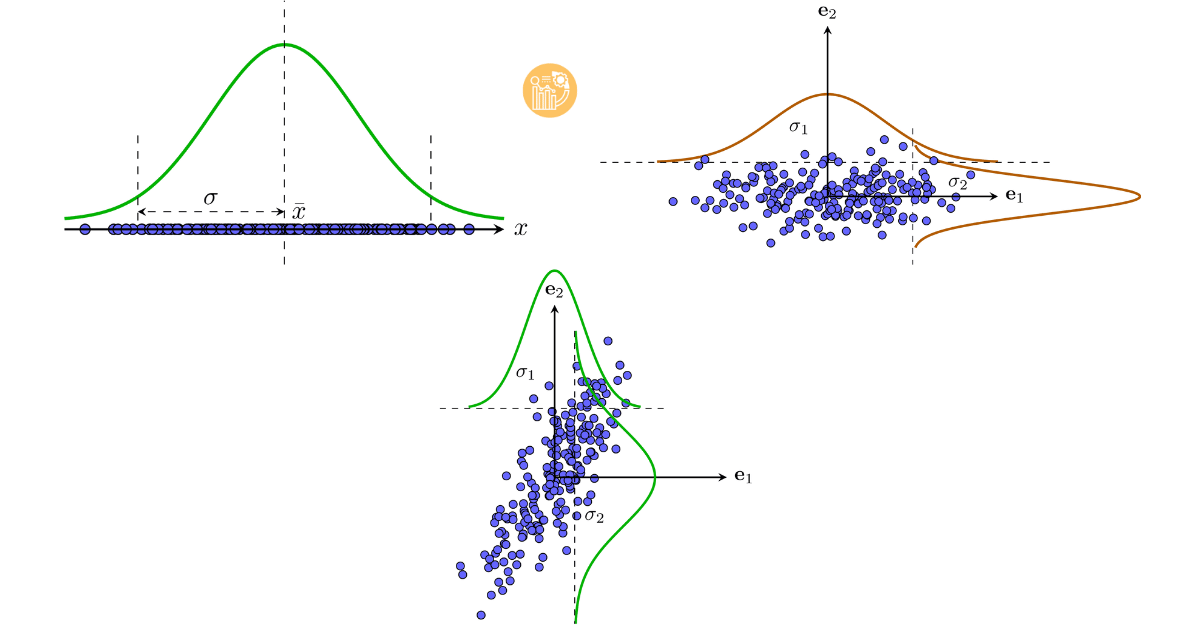
Ví dụ về kỳ vọng và phương sai. a) Trong không gian 1 chiều. b) Không gian 2 chiều mà hai chiều không tương quan. Trong trường hợp này, ma trận hiệp phương sai là ma trận đường chéo với hai phần tử trên đường chéo là σ1, σ2, đây cũng chính là hai trị riêng của ma trận hiệp phương sai và là phương sai của mỗi chiều dữ liệu. c) Dữ liệu trong không gian hai chiều có tương quan. Theo mỗi chiều, ta có thể tính được kỳ vọng và phương sai. Phương sai càng lớn thì dữ liệu trong chiều đó càng phân tán. Trong ví dụ này, dữ liệu theo chiều thứ hai phân tán nhiều hơn so so với chiều thứ nhất.

3. Principal Component Analysis (PCA)

Ý tưởng chính

PCA tìm hệ cơ sở mới (U) sao cho thông tin dữ liệu chủ yếu nằm ở một vài trục chính (principal components). Các chiều có phương sai nhỏ sẽ bị loại bỏ.

Ví dụ: Nếu bạn có 2 camera chụp một người — ảnh chính diện chứa nhiều thông tin hơn ảnh chụp từ trên đầu → có thể bỏ ảnh thứ hai mà không mất mát đáng kể thông tin.

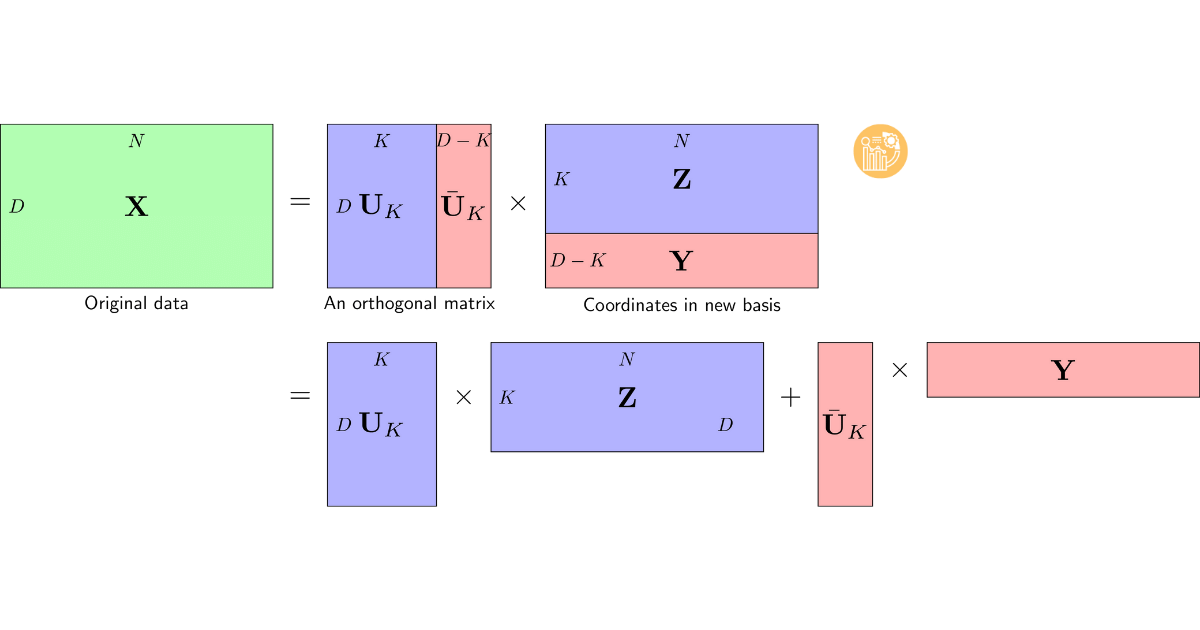
Ý tưởng chính của PCA: Tìm một hệ trực chuẩn mới sao cho trong hệ này, các thành phần quan trọng nhất nằm trong K thành phần đầu tiên.

Biểu diễn PCA

U = [Uₖ, Ūₖ]
X = UₖZ + ŪₖY
Z = UₖᵀX,   Y = ŪₖᵀX

Ta muốn tìm U sao cho phần ŪₖY là ít thông tin nhất.

Sau khi chuẩn hoá dữ liệu (trừ trung bình):

Ẋ = X - x̄·1ᵀ

Mục tiêu tối ưu PCA là:

min_U ||X - UₖZ||_F²

Tương đương với:

J = ∑_i=K+1^D uᵢᵀ S uᵢ

Định lý chính

Định lý: Hàm F = ∑_i=1^K uᵢᵀ S uᵢ đạt giá trị lớn nhất khi uᵢ là các vector riêng ứng với K trị riêng lớn nhất của S.

Khi đó:

λ₁, λ₂, …, λₖ: các thành phần chính (principal components).
PCA giữ lại các chiều có phương sai lớn nhất → chứa nhiều thông tin nhất.

Góc nhìn thống kê

PCA có thể hiểu như một phép xoay hệ trục sao cho dữ liệu tập trung chủ yếu vào vài trục chính. Các trục còn lại có phương sai rất nhỏ, có thể bỏ qua mà không ảnh hưởng nhiều.

Tổng phương sai giữ lại:

Variance_retained = ∑λ_i (i = 1 → K)

Quy trình PCA

Chuẩn hóa dữ liệu: trừ mỗi vector cho giá trị trung bình.
Tính ma trận hiệp phương sai: S = (1/N) ẊẊᵀ.
Tính trị riêng và vector riêng của S.
Chọn K vector riêng lớn nhất tương ứng với K trị riêng lớn nhất.
Chiếu dữ liệu vào không gian mới: Z = UₖᵀẊ.
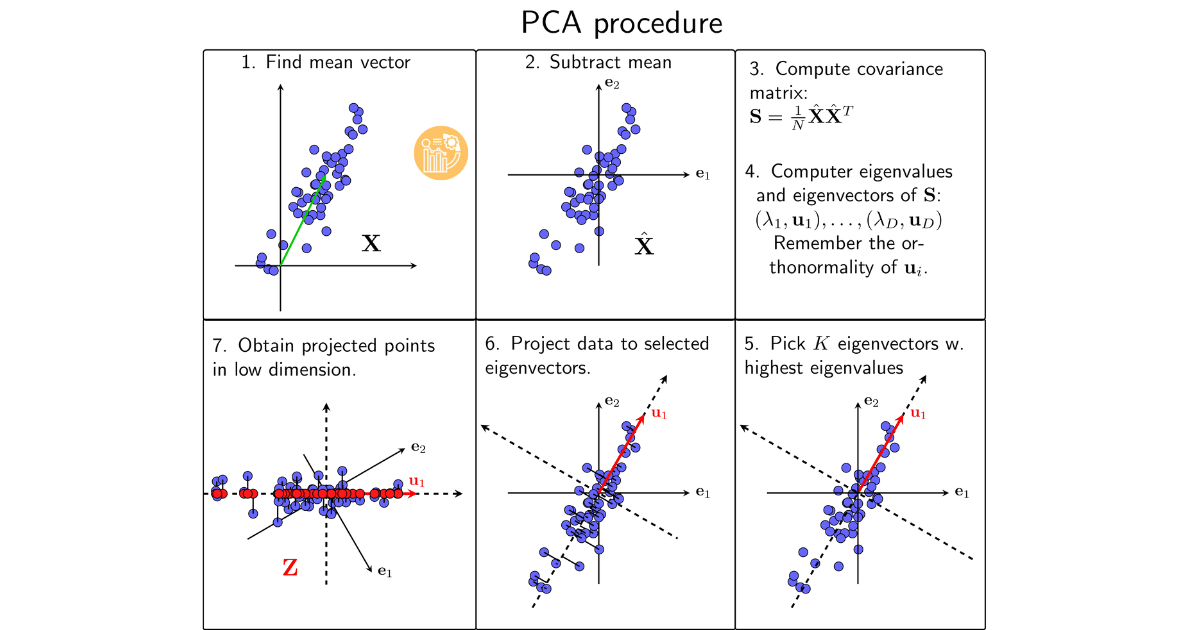
Các bước thực hiện PCA

Ghi chú

Tổng phương sai trong mọi hệ cơ sở là không đổi.
PCA không cần giả định phân phối dữ liệu, chỉ dựa vào phương sai.
Ứng dụng của PCA:
- Giảm số chiều trước khi huấn luyện mô hình ML
- Trực quan hóa dữ liệu đa chiều
- Giảm nhiễu, nén dữ liệu

Kết luận

PCA là phương pháp giảm chiều tuyến tính mạnh mẽ và trực quan, giúp giữ lại phần lớn thông tin của dữ liệu, giảm số chiều tính toán, đồng thời dễ dàng phát hiện cấu trúc ẩn trong dữ liệu.

Khám phá Dịch vụ SPSS tại: Dịch vụ chạy SPSS | Uy tín & Hiệu quả

Xem thêm: Hướng dẫn phân tích thành phần chính PCA – Phần 2

Khám phá Dịch vụ SPSS tại: Dịch vụ chạy SPSS | Uy tín & Hiệu quả