Trong quá trình nghiên cứu và xử lý dữ liệu, PCA đã trở thành công cụ mạnh mẽ để giảm chiều dữ liệu, khai thác đặc trưng và trực quan hóa. Phần 2 của bài viết này sẽ đi sâu vào mối quan hệ giữa PCA và SVD, cách lựa chọn Thành phần chính thứ hai, các phương pháp nâng cao và những ứng dụng thực tế. Đối tượng hướng tới không chỉ là người mới bắt đầu mà còn những nhà phân tích dữ liệu muốn nâng cao kiến thức về PCA và các kỹ thuật mở rộng. Với nội dung giàu tính học thuật và thực hành, chúng ta sẽ cùng khám phá các lý thuyết đi kèm các ví dụ thực tế bằng Python.
Ở bài viết này ta mở rộng từ phần 1 để xem mối liên hệ giữa PCA và SVD, cách chọn chiều K, một số lưu ý thực tế và hai ứng dụng tiêu biểu: Eigenface và Unsupervised Anomaly Detection.
Mục lục
Toggle1. Mối liên hệ giữa PCA và SVD
1.1. SVD và xấp xỉ ma trận hạng thấp
Nếu cần xấp xỉ một ma trận X bằng một ma trận A có hạng không vượt quá k, nghiệm tối ưu chính là Truncated SVD:
Nếu X = U Σ V^T thì xấp xỉ hạng-k là A = U_k Σ_k V_k^T.
1.2. Ý tưởng PCA
PCA tìm ma trận trực giao U_k và biểu diễn thấp chiều Z để tối thiểu hóa sai số tái tạo:
min_{U_k,Z} ||X - U_k Z||_F s.t. U_k^T U_k = I
1.3. Kết luận
Khi dữ liệu đã được chuẩn hóa (mean = 0), nghiệm PCA rút ra trực tiếp từ Truncated SVD: U_k là các cột đầu của ma trận U trong SVD và Z = Σ_k V_k^T. Do đó, về bản chất, PCA là một trường hợp đặc biệt của SVD.
2. Cách chọn số chiều K
Một phương pháp phổ biến là dựa vào tỉ lệ phương sai được giữ lại. Nếu λ1..D là các trị riêng giảm dần của ma trận hiệp phương sai, thì:
rK = (Σi=1..K λi) / (Σj=1..D λj)
Chọn K nhỏ nhất sao cho r_K đạt ngưỡng mong muốn (ví dụ 0.95 hoặc 0.99). Khi dữ liệu nằm gần một subspace, vài trị riêng đầu thường chiếm phần lớn phương sai — khi đó K có thể rất nhỏ.
3. Lưu ý khi áp dụng PCA trong thực tế
3.1. Trường hợp D > N (số chiều nhiều hơn số mẫu)
Khi D > N, ma trận hiệp phương sai S = (1/N) X X^T có hạng ≤ N. Thay vì tính trị riêng của S (kích thước D×D), ta có thể tính trị riêng của T = X^T X (kích thước N×N) rồi suy ra vector riêng của S bằng X u. Cách này tiết kiệm bộ nhớ và thời gian.
3.2. Chuẩn hóa các vector riêng
Với ma trận đối xứng, vector riêng tương ứng với các trị riêng khác nhau là trực giao. Kết hợp Gram–Schmidt, ta chuẩn hóa để thu được hệ trực chuẩn U_k cho PCA.
3.3. PCA quy mô lớn (Large-scale PCA)
Với dữ liệu rất lớn (triệu ảnh, nghìn chiều), tính trực tiếp trị riêng không khả thi. Power Iteration là một phương pháp xấp xỉ nhanh trị riêng lớn nhất. Dùng deflation để tìm các trị riêng kế tiếp. Kỹ thuật này được dùng trong nhiều hệ thống quy mô lớn (ví dụ PageRank).
4. Ví dụ minh họa
4.1. Eigenface — nén ảnh khuôn mặt bằng PCA

Eigenface là ứng dụng kinh điển của PCA trong nhận dạng khuôn mặt. Mỗi ảnh (ví dụ 116×98 = 11.368 chiều) có thể được nén xuống vài trăm chiều với PCA, giữ đặc trưng cần thiết cho nhận dạng.
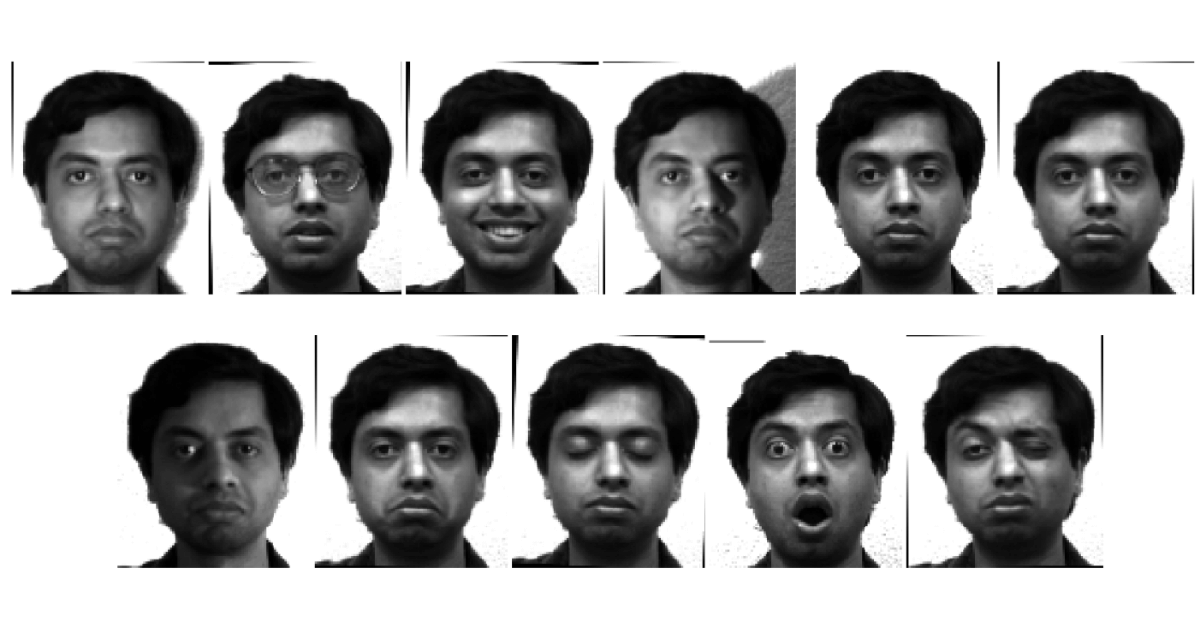
Ví dụ về ảnh của một người trong Yale Face Database
Đoạn mã minh họa dùng sklearn (lưu ý: sklearn xử lý mẫu theo hàng — nếu dữ liệu bạn theo cột, hãy transpose):
import numpy as np
from scipy import misc
from sklearn.decomposition import PCA
path = 'unpadded/'
ids = range(1, 16)
states = ['centerlight','glasses','happy','leftlight','noglasses','normal',
'rightlight','sad','sleepy','surprised','wink']
h, w, K = 116, 98, 100
D, N = h*w, len(states)*15
X = np.zeros((D, N))
cnt = 0
for i in ids:
for s in states:
fn = f"{path}subject{str(i).zfill(2)}.{s}.pgm"
X[:, cnt] = misc.imread(fn).reshape(D)
cnt += 1
pca = PCA(n_components=K)
pca.fit(X.T)
U = pca.components_.T
Khi tái tạo ảnh từ K = 100 thành phần chính, ảnh thu được sẽ có nhiễu nhưng vẫn giữ các đặc trưng khuôn mặt — cho thấy PCA nén dữ liệu hiệu quả.

Các eigenfaces tìm được bằng PCA.

Hàng trên: các ảnh gốc. Hàng dưới: các ảnh được suy ra từ eigenfaces. Ảnh ở hàng dưới có nhiều nhiễu nhưng vẫn mang những đặc điểm riêng mà mắt người có thể phân biệt được.
4.2. Phát hiện bất thường (Unsupervised Anomaly Detection) với PCA
Ý tưởng: các điểm “normal” nằm gần một subspace; các điểm “abnormal” nằm xa subspace đó. Thực hiện PCA trên toàn bộ dữ liệu, tính khoảng cách của mỗi điểm tới subspace được tạo bởi các thành phần chính; điểm có khoảng cách lớn được coi là bất thường.
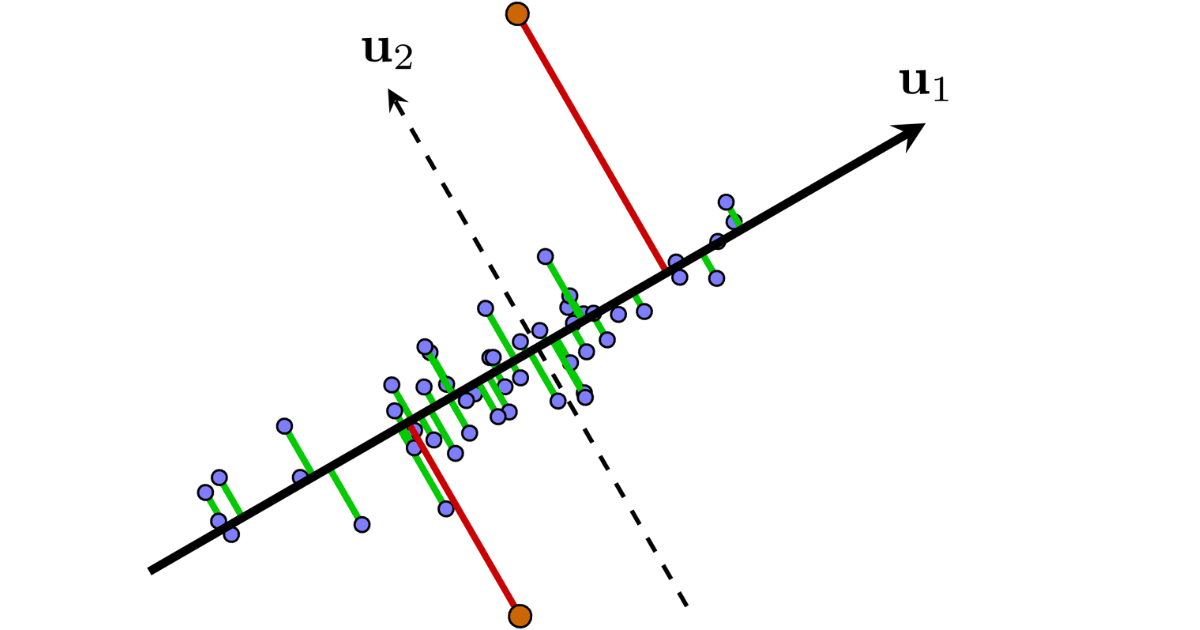
PCA cho việc xác định các sự kiện ‘abnormal’ với giả sử rằng các sự kiện ‘normal’ chiếm đa số và nằm gần trong một không gian con nào đó. Khi đó, nếu làm PCA trên toàn bộ dữ liệu, không gian con thu được gần với không gian con của tập các sự kiện ‘normal’. Lúc này, các điểm quá xa không gian con này, trong trường hợp này là các điểm màu cam, có thể được coi là các sự kiện ‘abnormal’.
5. Thảo luận & Gợi ý mở rộng
- PCA là phương pháp unsupervised — không tận dụng nhãn. Nếu mục tiêu là phân biệt lớp, cân nhắc dùng LDA hoặc các phương pháp supervised khác.
- Với dữ liệu lớn, dùng Incremental PCA hoặc Randomized SVD để giảm tiêu thụ bộ nhớ và tăng tốc.
- Các biến thể hữu ích: Sparse PCA, Kernel PCA, Robust PCA tùy ngữ cảnh.