Trong thế giới dữ liệu ngày nay, mô hình hồi quy là công cụ không thể thiếu giúp các nhà phân tích, nhà khoa học dữ liệu và các chuyên gia dự đoán xu hướng, phân tích mối quan hệ giữa các biến số, và cung cấp cái nhìn sâu sắc về các hiện tượng phức tạp. Mô hình hồi quy có thể ứng dụng trong nhiều lĩnh vực như kinh tế, tài chính, y học, và bất động sản, nơi các nhà nghiên cứu và doanh nghiệp cần biến dữ liệu thô thành những thông tin giá trị và dễ dàng ứng dụng vào thực tế.
Trong bài viết này, chúng ta sẽ đi sâu vào các khái niệm cốt lõi, các loại mô hình phổ biến, quy trình xây dựng, cũng như các kỹ thuật nâng cao và thực hành thực tế để xây dựng mô hình hồi quy bằng Python. Ngoài ra, bài viết còn dành phần để phân tích những hạn chế, các vấn đề cần chú ý, giúp bạn đọc có cái nhìn toàn diện về công cụ phân tích này. Với tầm quan trọng và phạm vi ứng dụng rộng lớn, hiểu rõ về mô hình hồi quy chính là chìa khóa để tiếp cận dữ liệu một cách sáng tạo, hiệu quả và khoa học hơn trong mọi lĩnh vực.
Mục lục
ToggleMô Hình Hồi Quy Là Gì?
Mô hình hồi quy là phương pháp thống kê giúp xác định mối quan hệ giữa một biến phụ thuộc (biến cần dự đoán) và một hoặc nhiều biến độc lập (các yếu tố ảnh hưởng). Mục đích chính của mô hình hồi quy là giúp dự đoán các kết quả từ những yếu tố đầu vào, đồng thời giải thích mối quan hệ giữa các yếu tố này. Đây là công cụ quan trọng trong việc đưa ra quyết định chiến lược, từ kinh tế đến nghiên cứu khoa học.
Các lĩnh vực ứng dụng chính
- Kinh tế: Dự đoán doanh thu, giá cổ phiếu.
- Tài chính: Phân tích rủi ro, định giá tài sản.
- Y học và Khoa học tự nhiên: Nghiên cứu mối quan hệ giữa các yếu tố sinh học và sức khỏe.
- Bất động sản: Định giá nhà đất và dự đoán xu hướng thị trường.
Mô hình hồi quy rất linh hoạt, giúp phân tích các mối quan hệ giữa các yếu tố và đưa ra các dự đoán chính xác hơn trong mọi lĩnh vực.
Lịch sử phát triển
Lịch sử của mô hình hồi quy kéo dài hơn một thế kỷ, bắt nguồn từ các nghiên cứu thống kê ban đầu của Francis Galton, ông đã quan sát và nhận thấy mối liên hệ giữa chiều cao cha mẹ và con cái. Từ những quan sát này, các nhà thống kê bắt đầu phát triển các kỹ thuật mô hình hóa tuyến tính đầu tiên, rồi dần mở rộng sang các dạng phức tạp hơn như hồi quy đa biến, hồi quy phi tuyến, và các kỹ thuật tối ưu khác.
Trong thập niên 20 và 30 của thế kỷ 20, các nhà thống kê như Ronald Fisher đã đóng góp quan trọng trong việc chuẩn hóa các phương pháp ước lượng và kiểm định giả thuyết cho mô hình hồi quy. Sự phát triển của máy tính và các thuật toán tối ưu linh hoạt hơn trong những thập kỷ gần đây đã giúp mở rộng khả năng áp dụng của mô hình hồi quy vào những dữ liệu lớn, phức tạp. Hiện nay, mô hình hồi quy đã trở thành một phần không thể thiếu trong các hệ thống phân tích dữ liệu, phục vụ trong đa dạng lĩnh vực khoa học, kinh doanh và công nghệ.
Các loại mô hình hồi quy phổ biến
Trong phân tích dữ liệu, có rất nhiều dạng mô hình hồi quy phù hợp với các đặc thù và yêu cầu của từng bài toán. Từ mô hình tuyến tính đơn biến đơn giản đến các dạng phức tạp hơn, mỗi loại đều có ưu thế riêng, cũng như giới hạn cần lý giải cẩn trọng. Các nhà phân tích cần chọn lọc mô hình phù hợp dựa trên các giả định, tính chất của dữ liệu và mục tiêu dự báo.
Trong phần này, chúng ta sẽ đi sâu vào các loại mô hình chính, bắt đầu từ mô hình hồi quy tuyến tính đơn biến, mở rộng sang mô hình đa biến và cuối cùng là các mô hình phi tuyến nâng cao. Bên cạnh đó, việc hiểu rõ đặc điểm từng dạng sẽ giúp bạn chọn đúng công cụ phù hợp cho từng bài toán cụ thể, từ đó nâng cao độ chính xác và tính khả thi của dự báo.
1. Mô hình hồi quy tuyến tính đơn biến
Mô hình hồi quy tuyến tính đơn biến là dạng cơ bản nhất, khi chỉ sử dụng một biến độc lập để dự đoán biến phụ thuộc. Đây là điểm khởi đầu quen thuộc cho những ai mới bắt đầu học về hồi quy, đồng thời cũng là kỹ thuật dễ hiểu và dễ triển khai trong thực tế. Đặc điểm nổi bật của mô hình này là khả năng thể hiện mối liên hệ tuyến tính rất rõ ràng và trực quan, trên đồ thị có thể biểu diễn bằng một đường thẳng.
Đặc điểm và công thức mô hình
Mô hình hồi quy tuyến tính đơn biến là dạng cơ bản nhất, chỉ sử dụng một biến độc lập để dự đoán biến phụ thuộc. Công thức mô hình này là:
y= w0 + w1 * x + ε
Trong đó:
- y là biến phụ thuộc.
- x là biến độc lập.
- w0 là hệ số chặn, thể hiện giá trị kỳ vọng của y khi x=0.
- w1 là hệ số góc, chỉ ra mức độ ảnh hưởng của x đến y.
- ε là sai số ngẫu nhiên.
Ví dụ: Dự đoán giá nhà dựa trên diện tích. Giả sử có dữ liệu về diện tích và giá của các căn nhà, mô hình hồi quy tuyến tính đơn biến sẽ giúp xác định mối quan hệ giữa diện tích và giá trị nhà.
Ưu điểm & Nhược điểm
Ưu điểm rõ ràng là đơn giản, dễ hiểu, dễ triển khai, phù hợp cho các bài toán mà các yếu tố ảnh hưởng rõ ràng và tuyến tính. Ngoài ra, khả năng diễn giải của mô hình cũng là điểm mạnh, giúp các nhà phân tích đưa ra những kết luận mang tính chiến lược dựa trên các hệ số ước lượng.
Tuy nhiên, hạn chế lớn nhất của mô hình này là giả định rằng mối quan hệ giữa biến độc lập và biến phụ thuộc là tuyến tính, điều này không phải lúc nào cũng đúng trong thực tế. Nếu dữ liệu có mối quan hệ phi tuyến, mô hình này sẽ không thể cung cấp dự đoán chính xác, gây ra sai số lớn. Hơn nữa, khi có nhiều biến, độ phức tạp của mô hình tăng lên, việc kiểm soát các yếu tố nhiễu và đa cộng tuyến trở nên khó khăn hơn.
2. Mô hình hồi quy tuyến tính đa biến
THãy tưởng tượng bạn muốn dự đoán giá của một căn nhà dựa trên các đặc trưng như diện tích (x), số phòng ngủ (x), và tuổi nhà (x). Giả sử bạn đã thu thập dữ liệu về giá và diện tích của nhiều căn nhà (n căn) – mà ta gọi đây là tập dữ liệu huấn luyện. Chúng ta sẽ xây dựng một mô hình hồi quy tuyến tính đa biến để mô tả mối quan hệ giữa giá nhà và các đặc trưng này. Mô hình hồi quy tuyến tính đa biến cho bài toán trên được viết dưới dạng công thức sau:
y= w0 + w1 * x1 + w2 * x2 + w3 * x3 + ϵ
Trong đó:
- y: Biến phụ thuộc (dependent variable), hay còn gọi là biến phản hồi (response variable), hoặc nhãn (label). Đây chính là giá trị mà mô hình cần dự đoán từ tập dữ liệu huấn luyện. Ví dụ, trong bài toán này, ylà giá của căn nhà cần dự đoán.
- (x1, x2, x3): Các biến độc lập (independent variables), hay còn gọi là biến giải thích (explanatory variables), hoặc đặc trưng (features). Trong ví dụ trên, x1 có thể là diện tích căn nhà, x2 là số phòng ngủ, và x3 là tuổi của căn nhà.
- w0: Hệ số chặn (intercept), biểu thị giá trị kỳ vọng của y khi tất cả các biến độc lập đều bằng 0. Trong thực tế, w0 thường không có ý nghĩa cụ thể, nhưng nó giúp xác định vị trí của đường hồi quy trong không gian.
- (w1, w2, w3): Các hệ số góc (slope), thể hiện tác động của từng biến độc lập đến biến phụ thuộc. Ví dụ, w1 cho biết diện tích căn nhà ảnh hưởng như thế nào đến giá bán của nó.
- ϵ: Sai số ngẫu nhiên (error term), biểu thị sự khác biệt giữa giá trị thực tế và giá trị dự đoán. Sai số này bao gồm các yếu tố không thể đo lường hoặc chưa được đưa vào mô hình.
Công thức trên được gọi là mô hình hồi quy tuyến tính đa biến. Tổng quát, nếu có mmm biến độc lập (x1, x2,…, xm), công thức của mô hình hồi quy đa biến được viết lại như sau:
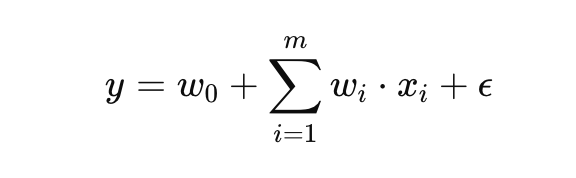
công thức hồi quy đa biến
Ví dụ:
Giả sử bạn có một bảng dữ liệu về giá trị của các căn nhà, bao gồm các đặc trưng như diện tích (m²), số phòng ngủ và tuổi của căn nhà. Bạn muốn dự đoán giá trị của căn nhà mới dựa trên các yếu tố này. Mô hình hồi quy tuyến tính đa biến sẽ cho phép bạn tính toán một giá trị dự đoán cho giá của căn nhà, dựa trên các hệ số ước lượng w0, w1, w2 và các đặc trưng x1, x2.
Ví dụ nếu:
- Diện tích căn nhà (x1) là 100 m²,
- Số phòng ngủ (x2) là 3 phòng,
- Tuổi của căn nhà (x3) là 10 năm,
Mô hình hồi quy sẽ tính toán giá dự đoán của căn nhà theo công thức đã cho.
Ưu Điểm Của Hồi Quy Tuyến Tính Đa Biến
- Đơn giản và dễ hiểu: Mô hình hồi quy tuyến tính đa biến là một trong những mô hình dễ hiểu và dễ triển khai, đặc biệt khi làm việc với dữ liệu có số lượng biến độc lập không quá lớn.
- Dễ giải thích: Các hệ số trong mô hình cung cấp thông tin cụ thể về mức độ ảnh hưởng của từng yếu tố (biến độc lập) đến kết quả (biến phụ thuộc). Điều này giúp người phân tích đưa ra những kết luận mang tính chiến lược.
- Ứng dụng rộng rãi: Mô hình hồi quy tuyến tính đa biến có thể áp dụng trong nhiều lĩnh vực như kinh tế, tài chính, y học, và nghiên cứu khoa học.
- Tính toán nhanh: Với dữ liệu không quá phức tạp, mô hình có thể được tính toán nhanh chóng và dễ dàng.
Nhược Điểm Của Hồi Quy Tuyến Tính Đa Biến
- Giả định tuyến tính: Mô hình giả định rằng mối quan hệ giữa các biến là tuyến tính. Tuy nhiên, trong thực tế, nhiều mối quan hệ có thể là phi tuyến, điều này sẽ làm giảm độ chính xác của mô hình nếu dữ liệu không tuân theo giả định tuyến tính.
- Nhạy cảm với đa cộng tuyến: Khi các biến độc lập có mối quan hệ mạnh với nhau, mô hình có thể gặp phải vấn đề đa cộng tuyến (multicollinearity), khiến việc ước lượng các hệ số trở nên không ổn định và gây khó khăn trong việc giải thích mô hình.
- Không xử lý tốt với dữ liệu nhiễu: Mô hình hồi quy tuyến tính đa biến có thể không hoạt động tốt khi dữ liệu chứa nhiều nhiễu hoặc ngoại lai (outliers), điều này có thể làm sai lệch kết quả dự đoán.
- Độ chính xác bị giảm khi số lượng biến lớn: Khi số lượng biến độc lập tăng lên quá mức, mô hình có thể trở nên phức tạp và dễ bị overfitting (quá khớp), đặc biệt là khi không có đủ dữ liệu huấn luyện.
3. Ước Tính Hệ Số Của Mô Hình Hồi Quy Tuyến Tính
Để ước tính hệ số của mô hình hồi quy tuyến tính, chúng ta sử dụng phương pháp tối thiểu hóa tổng sai số bình phương (Residual Sum of Squares – RSS). Mục tiêu là tìm giá trị của các hệ số sao cho tổng sai số này là nhỏ nhất. Công thức mô tả hàm mất mát (loss function) như sau:
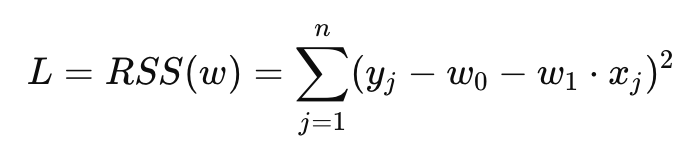
Để tìm ra giá trị w0 và w1, chúng ta áp dụng phương pháp đạo hàm và giải phương trình đạo hàm bằng 0 để tối thiểu hóa hàm mất mát:
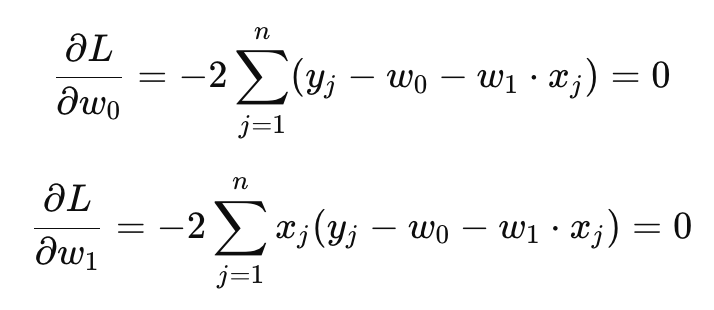
Giải phương trình này, ta tìm được các giá trị của w0 và w1:
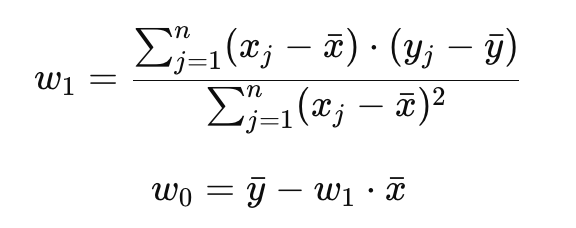
Trong đó, xˉ và yˉ lần lượt là giá trị trung bình của các biến x và y.
Phương pháp này giúp tìm ra các hệ số tối ưu cho mô hình hồi quy tuyến tính, giúp dự đoán chính xác hơn các giá trị mới dựa trên mối quan hệ tuyến tính giữa các biến.
4. Các Kỹ Thuật Nâng Cao Trong Mô Hình Hồi Quy
- Gradient Descent: Thuật toán tối ưu này giúp tìm kiếm các hệ số hồi quy tốt nhất khi xử lý các mô hình phi tuyến hoặc dữ liệu phức tạp. Thuật toán này hoạt động bằng cách giảm dần hàm mất mát qua từng vòng lặp.
- Regularization: Kỹ thuật này giúp ngăn chặn hiện tượng quá khớp bằng cách giảm độ phức tạp của mô hình, như Lasso hoặc Ridge.
Đánh Giá Hiệu Suất Mô Hình Hồi Quy Tuyến Tính
Sau khi xây dựng mô hình hồi quy tuyến tính và ước tính các hệ số, bước tiếp theo là đánh giá độ chính xác và hiệu quả của mô hình. Để làm điều này, chúng ta sẽ sử dụng một số chỉ số phổ biến giúp kiểm tra mức độ phù hợp của mô hình với dữ liệu thực tế. Các chỉ số đánh giá hiệu suất quan trọng bao gồm:
- R-squared (R²): Chỉ số này phản ánh tỷ lệ phần trăm phương sai của biến phụ thuộc (y) được mô hình giải thích. Một giá trị R² gần 1 cho thấy mô hình giải thích tốt mối quan hệ giữa các yếu tố và biến phụ thuộc.
- R-squared điều chỉnh: Khác với R², giá trị này điều chỉnh cho số lượng biến độc lập trong mô hình, giúp tránh việc mô hình trở nên quá phức tạp và có thể bị overfitting (quá khớp).
- Sai số bình phương trung bình (MSE): Đây là chỉ số đo lường độ lệch giữa các giá trị thực tế và giá trị dự đoán. MSE thấp cho thấy mô hình có khả năng dự đoán chính xác hơn.
- Sai số bình phương trung bình căn bậc hai (RMSE): RMSE được tính bằng căn bậc hai của MSE, giúp phản ánh độ lệch chuẩn của sai số dự đoán, và dễ dàng so sánh với đơn vị đo lường ban đầu của biến phụ thuộc.
Ví Dụ Minh Họa
Giả sử bạn muốn dự đoán giá trị của các căn nhà dựa trên các đặc trưng như diện tích, số phòng ngủ và tuổi nhà. Sau khi thu thập dữ liệu, mô hình hồi quy tuyến tính sẽ được huấn luyện để tìm mối quan hệ giữa các đặc trưng và giá nhà. Để đánh giá độ chính xác của mô hình, chúng ta có thể tính toán MSE và R², giúp đánh giá mức độ phù hợp của mô hình.
Dưới đây là mã Python sử dụng thư viện scikit-learn để tính toán và đánh giá mô hình hồi quy tuyến tính:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# STEP 1: Data preparation
df = pd.read_csv('Housing.csv')
X = df['area'].values.reshape(-1,1)
y = df['price'].values
# STEP 2: Model Training
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = LinearRegression()
model.fit(X_train, y_train)
# STEP 3: Prediction
y_predicted = model.predict(X_test)
# STEP 4: Evaluation
mse = mean_squared_error(y_test, y_predicted)
r2 = r2_score(y_test, y_predicted)
print("Mean Squared Error (MSE):", mse)
print("R-squared:", r2)
Kết quả:
- MSE: 367.52866047681846
- R²: 0.2728785187197468
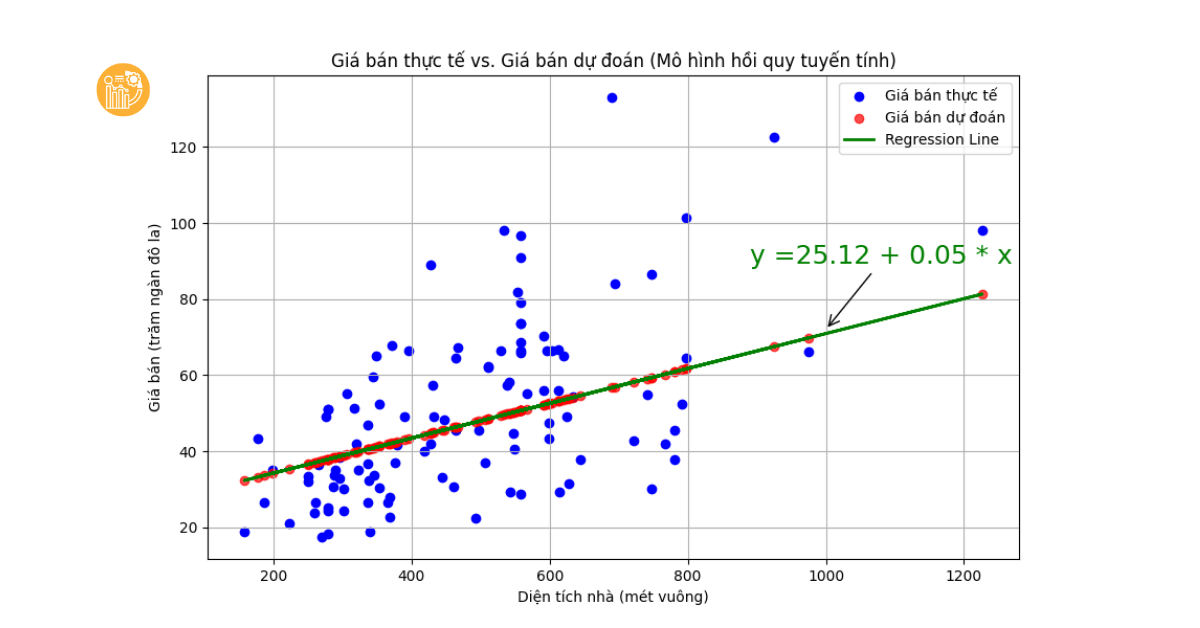
Từ kết quả trên, MSE cho biết mức độ chính xác của mô hình trong việc dự đoán giá trị thực tế, trong khi R-squared cho thấy phần trăm phương sai của giá trị y được mô hình giải thích. Cả hai chỉ số này đều giúp chúng ta hiểu rõ hơn về khả năng dự đoán của mô hình.
Kết luận
Mô hình hồi quy là công cụ quan trọng trong phân tích dữ liệu, giúp dự đoán và giải thích các mối liên hệ giữa các yếu tố, từ đó đưa ra các quyết định chiến lược phù hợp. Từ dạng đơn biến, đa biến đến phi tuyến, mỗi loại mô hình đều phù hợp với những bài toán và tập dữ liệu khác nhau, yêu cầu kỹ năng chọn lựa, tối ưu và đánh giá phù hợp.
Việc xây dựng mô hình đòi hỏi sự chuẩn bị dữ liệu bài bản, kỹ thuật ước lượng chính xác cùng các kỹ thuật nâng cao giúp tránh quá khớp, đa cộng tuyến hoặc các giả định sai lệch. Trong khi đó, hạn chế về giả định tuyến tính hay sensitivity với nhiễu phải luôn được chú ý để nhận diện rõ giới hạn của từng mô hình.
Trong xu hướng phát triển của khoa học dữ liệu và trí tuệ nhân tạo, mô hình hồi quy vẫn giữ vai trò trung tâm, là nền tảng để phát triển các kỹ thuật mới phức tạp hơn nhưng vẫn giữ được khả năng giải thích rõ ràng. Việc nắm vững và ứng dụng thành thạo các kỹ thuật này sẽ giúp bạn khai thác giá trị của dữ liệu một cách hiệu quả, sáng tạo và bền vững hơn trong tương lai















