Hồi quy tuyến tính, hay còn gọi là mô hình hồi quy tuyến tính (Linear Regression Model) | OLS là gì? Nó là một công cụ quan trọng trong kinh tế lượng. Nó là một phương pháp thống kê cho phép mô hình hóa mối quan hệ giữa một biến liên tục và một hoặc nhiều biến liên tục, định danh hoặc phân loại có liên quan. Nói một cách đơn giản, hồi quy tuyến tính là một phương pháp tiếp cận tuyến tính để dự đoán biến phụ thuộc (Y) dựa trên các biến giải thích hoặc biến độc lập (X).
Mục lục
Toggle1. Mô Hình Hồi Quy Tuyến Tính | OLS Là Gì?
1.1. Định Nghĩa
Hồi quy tuyến tính (Linear Regression) là một công cụ thống kê quan trọng để phân tích và dự đoán dữ liệu. Nó mô hình hóa mối quan hệ giữa một biến liên tục và một hoặc nhiều biến khác, có thể là liên tục, định danh hoặc phân loại. Nói một cách dễ hiểu, hồi quy tuyến tính là một phương pháp tiếp cận tuyến tính để dự đoán biến phụ thuộc Y (biến kết quả) trên trục tung dựa trên các biến độc lập X (biến giải thích) trên trục hoành.
Trong lĩnh vực thống kê, hồi quy tuyến tính là một phương pháp tiếp cận để mô hình hóa mối quan hệ giữa một biến phản hồi (biến phụ thuộc) và một hoặc nhiều biến giải thích (biến độc lập).
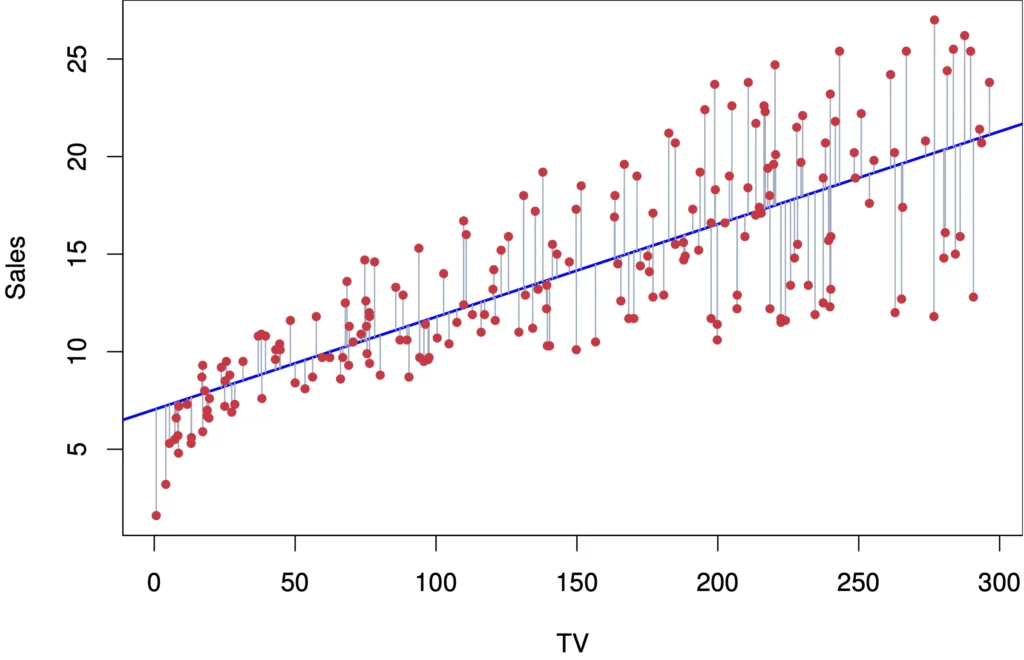
1.2. Xây Dựng Phương Trình Hồi Quy Tuyến Tính Tổng Quát
Chúng ta bắt đầu với mô hình hồi quy tuyến tính bội (multiple regression model), được biểu diễn dưới dạng mô hình hồi quy tổng thể (population regression model) với n – 1 biến giải thích:
Yi = β1 + β2X2i + β3X3i + … + βnXni + ui (Mô hình 1)
Trong đó:
- Y: Biến phụ thuộc (dependent variable) hoặc regressand.
- X: Các biến giải thích hoặc biến độc lập (explanatory variables / independent variables), còn được gọi là predictors, covariates hoặc regressors.
- βn: Hệ số của các biến độc lập, trong đó β1 là hệ số tự do.
- u: Hạng nhiễu hoặc sai số ngẫu nhiên (random hoặc stochastic error term).
- i: Ký hiệu cho quan sát thứ i trong tổng thể.
Phương trình trên có thể được viết gọn lại thành mô hình tổng thể (population model hoặc true model) như sau:
Yi = βX + ui (Mô hình 2)
với βX = β1 + β2X2i + β3X3i + … + βnXni
Trong đó:
- βX: Thành phần tất định (deterministic component), được giải thích như một trung bình có điều kiện (conditional mean) của Yi, tức là E(Yi|X): giá trị trung bình của Y khi X được cho trước.
- ui: Thành phần phi hệ thống (nonsystematic component) hoặc thành phần ngẫu nhiên (random component).
Mô hình tổng thể (population) đề cập đến một chủ thể được xác định rõ, ví dụ như các công ty, quốc gia, con người, là trọng tâm trong phân tích kinh tế lượng hoặc xác suất thống kê.
Ví dụ minh họa bằng phương trình hồi quy tuyến tính trong thực tế:
Xét một mẫu gồm 5 đứa trẻ với tuổi và chiều cao khác nhau như sau:
Giả sử chúng ta dự đoán chiều cao theo tuổi của từng bé và mô phỏng rằng phương trình hồi quy tuyến tính sẽ có dạng:
Y = β0 + β1*X
Trong đó, β1 là độ dốc (slope); β0 là điểm cắt (intercept); Y đại diện cho chiều cao và X đại diện cho tuổi của các bé.
| 5 đứa trẻ | Tuổi (X) | Chiều cao (cm) (Y) | Dự đoán (Y- Chiều cao) |
|---|---|---|---|
| Vinh | 6 | 80 | β0 + β1*6 |
| Đăng | 7 | 100 | β0 + β1*7 |
| Long | 8 | 120 | β0 + β1*8 |
| Khoa | 9 | 130 | β0 + β1*9 |
| Hân | 10 | 140 | β0 + β1*10 |
Bảng 1.1. Mẫu phương trình hồi quy tuyến tính
Chúng ta có thể sử dụng các công cụ thống kê như Excel, SAS, R, Stata, SPSS… để tìm ra các hằng số β0 và β1, là kết quả dự đoán (predict) của hàm hồi quy tuyến tính.
| Giá trị | Giải thích | |
|---|---|---|
| Độ lệch chuẩn của X | 1,5811 | Dùng hàm =STDEV (giá trị X) trong Excel |
| Độ lệch chuẩn của Y | 24,0831 | Dùng hàm =STDEV (giá trị Y) trong Excel |
| Trung bình X | 8 | Dùng hàm Average=(X) trong Excel |
| Trung bình Y | 114 | Dùng hàm Average=(Y) trong Excel |
| Tương quan giữa X và Y | 0,9847 | Dùng hàm =CORREL(tuổi, chiềucao) trong Excel |
| R2 (R – Square) | 0.9698 ~ 0.97 | Dùng hàm =RSQ(tuổi, chiều cao) trong Excel |
Bảng 1.2. Tìm các giá trị cần thiết để áp dụng vào công thức từ RSS trong Excel
Công thức tổng bình phương của phần dư RSS (Residual Sum of Squares): ∑(ei) =∑(Yi– βX – α)2
Tính toán β1 và β0 từ kết quả trên:
β1 = Hệ số tương quan ( Độ lệch chuẩn của Y / Độ lệch chuẩn của X) = 0,9847 (24,0831/1,5811) = 14,9988
β0 = Trung bình (Y) – β1 Trung bình (X) = 114 – 14,9988 8 = -5,9904
Bảng 1.3. Kết quả áp dụng công thức của β1* và β0*
Vậy, ta có phương trình hồi quy tuyến tính bậc 1: Y = -5,9904 + 14,9988X. Thay X là tuổi vào để tính các giá trị cần dự đoán ở Bảng 1.1:
| 5 đứa trẻ | Tuổi (X) | Chiều cao (cm) (Y) | Dự đoán (Y- Chiều cao) |
|---|---|---|---|
| Vinh | 6 | 80 | 84,0024 |
| Đăng | 7 | 100 | 99,0012 |
| Long | 8 | 120 | 114 |
| Khoa | 9 | 130 | 128,9988 |
| Hân | 10 | 140 | 143,9976 |
Bảng 1.4. Kết quả dự đoán bằng Excel hoặc máy tính CASIO
Từ kết quả trên, ta vẽ được biểu đồ với đường hồi quy tuyến tính.
Có thể để ý từ kết quả dự đoán tại đứa trẻ Long là 114 có sự thay đổi hướng lên hoặc cùng 1 đường thẳng với các đứa trẻ còn lại vì mối quan hệ này không còn đúng chính xác 100% nữa mà chỉ đúng 97% theo như kết quả R-Square hay R2 trả về từ *bảng 4.2 phía trên. Sự sai lệch này trong thống kê gọi là (residual) hoặc sai số (errors) là ước lượng của hạng nhiễu. *Xem thêm: Hồi quy tuyến tính trong Machine Learning.
Đánh Giá Sức Mạnh của Mô Hình Hồi Quy Tuyến Tính
Sức mạnh của mô hình được đo lường thông qua hệ số xác định r2 (coefficient of determination) hay R-Square (R2), dao động từ 0 đến 1. Mô hình tốt thường có R2 trên 0.5, nghĩa là hơn 50% phương sai của biến phụ thuộc Y được dự đoán từ biến độc lập X. Nói cách khác, các biến độc lập giải thích được bao nhiêu phần trăm sự thay đổi của biến phụ thuộc.
Công thức tính R-Square (R2) là:
R2 = (TSS – RSS)/TSS
Trong đó:
- Tổng các bình phương (TSS): TSS đo lường tổng biến thiên trong biến phụ thuộc và có thể coi là lượng biến thiên vốn có trước khi thực hiện hồi quy.
- Tổng bình phương phần dư (RSS): RSS đo lường lượng biến đổi còn lại không giải thích được sau khi thực hiện hồi quy.
- Hiệu số TSS – RSS đo lường mức độ biến đổi trong biến phụ thuộc được giải thích (hoặc loại bỏ) bằng cách thực hiện hồi quy.
- Thang đo định danh (nominal scale): thường được dùng với các biến giả (dummy variables) hoặc biến phân loại (categorical variables) được lượng hoá thành 1 và 0 tuỳ theo sở thích người định danh. Các biến ví dụ như giới tính (gender), hôn nhân (marriage), tuổi dưới hay trên 20 (old), vùng miền (regions), tôn giáo (religion),…
Hãy xem hết các mục trên để các bạn tìm kiếm lời giải để áp dụng làm bài tập về hồi quy tuyến tính nhé!
2. Hiểu Rõ Bản Chất & Ý Nghĩa của OLS

2.1. Đặc Điểm của Biến Phụ Thuộc
Biến phụ thuộc được xem như một biến ngẫu nhiên liên tục và được đo lường bằng một trong 4 thang đo thông dụng trong phần mềm SPSS:
- Thang đo khoảng (interval scale): Ví dụ như khoảng cách thu nhập giữa người nghèo và người giàu, giữa các năm.
- Thang đo định danh: Đo các biến giả có giá trị được lượng hóa thành 0 và 1, ví dụ như giới tính, tôn giáo, hôn nhân.
- Thang đo thứ bậc (ordinal scale): Tương tự thang đo định danh, nhưng thêm thứ bậc cho biến, ví dụ như mức thu nhập (thấp -> cao), xếp hạng (A -> D).
- Thang đo tỷ lệ (ratio scale): Tỷ lệ giữa hai biến số, ví dụ như tỷ số giữa GDP năm nay và năm ngoái, lạm phát.
Thông tin thú vị: Trong kinh tế lượng cơ bản, mô hình hồi quy tuyến tính ước lượng theo phương pháp OLS (sẽ được đề cập bên dưới) thì biến Y chỉ ở dạng thang đo tỷ lệ hoặc thang đo khoảng (gọi chung là biến ngẫu nhiên liên tục). Lý do là sự thay đổi thang đo và phân phối xác suất của Y sẽ thay đổi thang đo của sai số u, mà sai số u không thể là thang đo thứ bậc và định danh.
2.2. Tìm Hiểu Về Biến Độc Lập
Các biến độc lập có thể được đo lường theo bất kỳ thang đo nào như biến phụ thuộc. Trong mô hình hồi quy tuyến tính cổ điển (CLRM), biến độc lập được xem là biến phi ngẫu nhiên (nonrandom); nghĩa là các giá trị của biến độc lập được giữ cố định khi lấy mẫu lặp đi lặp lại.
Vì vậy, phân tích hồi quy tuyến tính có điều kiện (conditional) là tính giá trị trung bình của biến phụ thuộc khi cho trước các giá trị của biến độc lập.
Lưu ý: Bạn có thể cho phép các biến độc lập là ngẫu nhiên giống như biến biến phụ thuộc, nhưng cần phải lưu ý về cách giải thích các kết quả hồi quy.
2.3. Bản Chất của Hạng Nhiễu và Sai Số Ngẫu Nhiên
Hạng nhiễu hoặc sai số ngẫu nhiên đại diện cho tất cả các biến mà bạn bỏ sót, có thể vì:
- Không có sẵn dữ liệu (lack of data availability): Ví dụ, khi điều tra các nhân tố ảnh hưởng đến thu nhập của gia đình, dữ liệu về công việc, tuổi có thể thu thập được nhưng tinh thần của thành viên tạo ra thu nhập lại khó thu thập.
- Lỗi đo lường trong dữ liệu (errors of measurement in the data): Ví dụ, đo lường sai về thu nhập trung bình của người dân TPHCM khi chỉ xét từ mức 100 triệu/tháng trở xuống.
Thông tin thú vị: Cho dù nguồn gốc của hạng nhiễu u là gì thì vẫn có giả định rằng ảnh hưởng trung bình của hạng nhiễu ngẫu nhiên lên biến phụ thuộc là không đáng kể.
2.4. Đặc Điểm của Hệ Số Hồi Quy
Các hệ số hồi quy là những con số cố định (fixed numbers) và không ngẫu nhiên (not random), mặc dù ta không thể biết giá trị thực của các hệ số này. Giá trị này tùy thuộc vào hoàn cảnh, đề tài và dữ liệu bạn thu thập.
Mục đích của phân tích hồi quy là ước lượng (estimate) các giá trị hệ số hồi quy dựa trên dữ liệu mẫu, và các ước lượng (estimators) của hệ số hồi quy là các biến ngẫu nhiên vì giá trị của từng hệ số sẽ thay đổi khi mẫu thay đổi.
Lưu ý: Các hệ số hồi quy có phân phối chuẩn nên khi kiểm định từng hệ số hồi quy ta thường sử dụng thống kê t thay vì thống kê z. Một nhánh của thống kê được biết là thống kê Bayes xử lý các hệ số hồi quy (tổng thể) là ngẫu nhiên. À quên nhớ tìm hiểu thêm phương pháp đồng nhất hệ số nữa nhé!
2.5. Ý Nghĩa Của Mô Hình Hồi Quy Tuyến Tính
Thuật ngữ tuyến tính trong mô hình hồi quy tuyến tính đề cập đến tổ hợp tuyến tính ở các hệ số hồi quy (linearity in the regression coefficients) chứ không phải tuyến tính ở biến phụ thuộc và độc lập.
Có thể bạn sẽ cần: Khi biến phụ thuộc Y và độc lập X ở dạng phi tuyến tính (nonlinear), một trong hai biến có thể ở dạng logarit cơ số e tự nhiên như ln(X), dạng bình phương X2, dạng tỷ lệ nghịch 1/X hoặc một số dạng khác.
2.6. Các Loại Dữ Liệu Thường Dùng Trong Mô Hình Hồi Quy Tuyến Tính
Có ba loại dữ liệu thường được sử dụng trong mô hình hồi quy tuyến tính:
- Dữ liệu chuỗi thời gian (time series): Dữ liệu được thu thập theo thời gian (ngày, quý, tháng, năm,…), ví dụ như chỉ số giá tiêu dùng, giá chứng khoán theo ngày, GDP theo năm hoặc quý, tỷ giá hối đoái.
Lưu ý: Dữ liệu chuỗi thời gian thường có 2 đặc trưng: các quan sát liên tục theo thời gian tương quan với nhau, dẫn đến tự tương quan (autocorrelation), và các chuỗi thường không dừng (nonstationarity), có thể làm xuất hiện hồi quy giả mạo (spurious regression).
- Dữ liệu chéo (cross-sectional): Dữ liệu được thu thập tại cùng một thời điểm. Dữ liệu chéo thường có phương sai thay đổi (heteroscedasticity) do ảnh hưởng bởi quy mô (size or scale effect).
- Dữ liệu bảng (panel data) (một loại đặc biệt của dữ liệu gộp, pooled data): Kết hợp dữ liệu thời gian và dữ liệu chéo, kết hợp các đặc trưng của cả hai. Ví dụ như nghiên cứu ảnh hưởng của COVID lên các ngân hàng (cross-sectional aspect) trên sàn HOSE trong giai đoạn 5 năm (time-series aspect).
3. Phân Tích Mô Hình Hồi Quy Tuyến Tính Đa Biến
Ở trên, chúng ta đã thảo luận về mô hình tuyến tính đơn, chỉ có một biến độc lập. Nếu xét nhiều hơn một biến độc lập, phương pháp phù hợp nhất là hồi quy tuyến tính đa biến (Multiple Regression Linear).
Về cơ bản, không có sự khác biệt lớn giữa hồi quy tuyến tính “đơn giản” và “đa biến”. Cả hai mô hình đều tuân theo nguyên tắc OLS và thuật toán để có được đường hồi quy tối ưu nhất. Vậy phương pháp OLS là gì?
3.1. Tìm Hiểu Phương Pháp Bình Phương Nhỏ Nhất (OLS)
Định Nghĩa
Mô hình hồi quy bằng phương pháp bình phương nhỏ nhất (Ordinary Least Squares – OLS) là một trường hợp đặc biệt của phương pháp bình phương nhỏ nhất tổng quát (Generalized Least Squares – GLS). Nó sử dụng để tìm đường hồi quy gần nhất với giá trị liên tục của biến phụ thuộc, bằng cách làm cho tổng bình phương các sai số (∑u2i ) nhỏ nhất.
Ý Nghĩa
Xét mô hình hồi quy mẫu (sample regression model) với dạng:
Yi = b1 + b2X2i+ b3X3i +…+ bkXki+ui (Mô hình 3)
Rút gọn thành mô hình tổng thể (population model):
Yi = bX + ui (Mô hình 4)
với bX = b1 + b2X2i + b3X3i + … + bnXni
Tương tự như βX trong mô hình tổng thể ở Mô hình 2 (tức là E(Y|X)) được giải thích như một hàm hồi quy tổng thể (population regression function, PRF), thì bX trong Mô hình 4 là hàm hồi quy mẫu (sample regression function, SRF).
Phương pháp OLS sẽ lựa chọn các hệ số beta hồi quy từ b1 đến bk sao cho bình phương sai số của mô hình (u) ước lượng là nhỏ nhất.
Các vấn đề trong dự báo mô hình hồi quy tuyến tính như các biến giải thích định tính, xác định dạng mô hình, kiểm định Wald, Chi bình phương, mô hình Logistic, Logit, Probit, ARCH, GARCH, tính dừng, sai phân, đồng liên kết, ARIMA, Vector tự hồi quy VAR, nội sinh, GMM, Phương pháp ước lượng hợp lý tối đa (ML)… sẽ được Xulysolieu trình bày trong phần sau.
3.2. Khám Phá Mô Hình Hồi Quy Tuyến Tính Cổ Điển
Mô hình hồi quy tuyến tính cổ điển (Classic Linear Regression Model – CLRM) là mô hình phổ biến nhất trong các nghiên cứu hiện nay, đặc biệt là trong các đề tài luận văn thạc sĩ. Mô hình này có 8 giả định khác nhau (Gujarati, 2004).
Theo định lý Gauss-Markov, ước lượng của OLS là ước lượng tuyến tính không thiên lệch, có tính nhất quán và hiệu quả nhất (BLUE), do đó không cần thiết phải thực hiện các kiểm định khác như trong sách của Gujarati.
3.3. Phương Sai và Sai Số Chuẩn Của Ước Lượng OLS
Phương sai (Variance) là thước đo sự biến thiên của hệ số ước lượng khi mẫu thay đổi. Độ lệch chuẩn (Standard Deviation) hay ký hiệu là SE là căn bậc hai của phương sai.
Lưu ý: Trong phân tích hồi quy tuyến tính, độ lệch chuẩn của một ước lượng được gọi là sai số chuẩn (standard error, ký hiệu là se(bk)), về mặt khái niệm thì hoàn toàn giống với độ lệch chuẩn.
Trong mô hình hồi quy tuyến tính, một giá trị ước lượng của phương sai của hạng nhiễu ui được tính như sau:
- Phương sai trên là tỷ lệ của tổng bình phương phần dư (RSS) chia cho (n – k) với bậc tự do (df), n là cỡ mẫu và k là số tham số hồi quy ước lượng; bao gồm một hệ số cắt (b1) và (k – 1) hệ số độ dốc (slope coefficients).
- Và ????̂ là sai số chuẩn của hồi quy (standard error of the regression, SER). Nó đơn giản là độ lệch chuẩn của các giá trị Y xoay quanh đường hồi quy và thường được xem như một thước đo về “mức độ phù hợp” (goodness of fit) của đường hồi quy ước lượng.
3.4. Phân Phối Xác Suất của Các Ước Lượng OLS
Mỗi ước lượng của các hệ số hồi quy trong mô hình theo phương pháp OLS được phân theo phân phối chuẩn. Do đó, trong các nghiên cứu thường sử dụng phân phối t (t probability distribution) thay vì phân phối chuẩn, nhưng khi cỡ mẫu tăng lên thì phân phối t tiến về phân phối chuẩn.
Cách tính phân phối t trong phần mềm Eviews hoặc Stata với giả thuyết H0 (zero conditional): Bk=0, tức là kiểm tra từng hệ số hồi quy có khác 0 theo mức ý nghĩa thống kê (significance level) hay không. Có 3 cách để kiểm định giả thuyết này:
- Cách 1: Xây dựng khoảng tin cậy 99%, 95%, hoặc 90% theo các mức ý nghĩa 1%, 5%, 10% và xem hệ số Bk nằm trong hay nằm ngoài khoảng tin cậy đó (nếu khoảng tin cậy chứa số 0 thì chúng ta chấp nhận giả thuyết H0, ngược lại thì bác bỏ H0).
- Cách 2: So sánh trị tuyệt đối |t| với giá trị t phê phán (critical t value), tra bảng t ở một mức ý nghĩa được chọn (thường là 5%). Nếu |t| |t|, và Eviews là prob.) với mức ý nghĩa α trong 3 mức 1%, 5%, 10% được chọn, nếu p > α thì chúng ta chấp nhận H0, ngược lại thì bác bỏ H0. (p-value có thể tính tay)
Tóm lại, cả 3 cách trên đều ra được chung 1 kết quả. Tuy nhiên, ngày nay người ta thường sử dụng phần mềm Stata hay Eviews, SPSS… để ra kết quả nhanh và chính xác.
4. Hướng Dẫn Chạy Hồi Quy Bằng OLS trong Stata

Trước khi chạy hồi quy bằng phương pháp bình phương nhỏ nhất OLS, bạn cần xác định dữ liệu của mình thuộc loại dữ liệu bảng (panel data) hay dữ liệu chuỗi thời gian (time-series) để khai báo cho phần mềm Stata.
Xulysolieu.info sử dụng bộ dữ liệu xlsl.dta để mô phỏng chạy hồi quy với hai cách chạy hồi quy OLS trong Stata như sau:
Phương Pháp 1: Sử Dụng Menu trong Stata
- Đầu tiên, chọn Statistics > Linear models and related > Linear regression.
- Sau đó, chọn biến phụ thuộc vào ô Dependent Variable (ở đây là CASH) và các biến độc lập vào ô Independent Variables.
- Tiếp theo, chọn tab Reporting và chọn ô Standardized beta coefficients để hiển thị hệ số hồi quy chuẩn hóa.
- Cuối cùng, nhấn OK và kết quả sẽ được hiển thị.
Phương Pháp 2: Sử Dụng Lệnh trong Stata
- Lệnh đơn giản để hồi quy OLS là regress (hoặc viết tắt là reg).
- Vẫn sử dụng bộ dữ liệu mosl.dta, ta có kết quả:
Kết quả tương tự như cách 1, nhưng cách 2 nhanh hơn.
5. Giải Thích Ý Nghĩa Mô Hình OLS & Cách Đọc Bảng Kết Quả trong Stata
Các Mục Cần Chú Ý Khi Đọc Bảng Hồi Quy:
- Prob > F = 0.0000: Mức ý nghĩa kiểm định F với giả thuyết H0: Các biến độc lập đồng thời bằng 0. Ở đây, ta bác bỏ H0, kết luận mô hình có ý nghĩa thống kê.
- R – squared = 0.1100: R bình phương – R2 (học trong Kinh tế lượng).
- Adj R-squared = 0.1018: R bình phương hiệu chỉnh, thể hiện các biến độc lập trong mô hình đang giải thích được khoảng 10.18% sự biến thiên của biến phụ thuộc CASH.
Chỉ số R hiệu chỉnh (Adj R-squared) là quan trọng để đánh giá độ mạnh yếu của mô hình. Tốt nhất là nó nên lớn hơn 50%.
- Coef.: Hệ số hồi quy của mỗi biến độc lập trong mô hình (Beta).
- Std. Err.: Sai số chuẩn.
- P > |t|: P-value, thể hiện mức ý nghĩa của mỗi biến độc lập.
P-value thường được so sánh với mức ý nghĩa 5%. Nếu P-value dưới mức này, biến độc lập có mối quan hệ với biến phụ thuộc (Lưu ý: Có thể so sánh với mức ý nghĩa 10% và 1%).
Phương Trình Hồi Quy Tuyến Tính:
CASH = 0.1754 – 0.0155*SIZE + 0.0090*PB -0.0345*LEV + 2.23e-06*CF + 0.0004*TANG
Trong bảng hồi quy, biến SIZE, PB và CF đạt ý nghĩa thống kê tại mức 1% (p-value = 0.0000 0).
- Biến TANG không có mối quan hệ với biến phụ thuộc CASH (p-value = 0.850 > 5%).
Diễn giải ý nghĩa:
- Khi SIZE (quy mô công ty) giảm 1, CASH (lượng tiền mặt) của công ty giảm 0.0155 lần (các yếu tố khác không đổi). Tương tự với LEV.
- Khi giá trị sổ sách trên thị trường (PB) tăng 1, lượng tiền mặt (CASH) của công ty tăng 0.0090 lần (các yếu tố khác không đổi). Tương tự với CF.
- Biến TANG (tỷ trọng tài sản cố định hữu hình) không đạt ý nghĩa thống kê nên mối quan hệ giữa TANG và CASH không xác định được.
Sau khi hồi quy xong mô hình, cần thực hiện các kiểm định khuyết tật như đa cộng tuyến VIF, phương sai thay đổi, tự tương quan, hệ số tương quan…
6. Tóm Tắt
Bài viết đã giới thiệu các phần chính:
- Mô hình hồi quy tuyến tính đơn giản.
- Bản chất và ý nghĩa của hồi quy tuyến tính.
- Mô hình hồi quy tuyến tính đa biến.
- Chạy hồi quy bằng phương pháp bình phương nhỏ nhất OLS trong Stata.
- Giải thích ý nghĩa mô hình OLS và cách đọc bảng kết quả hồi quy.














