Trong thế giới thống kê, độ lệch chuẩn (Standard Deviation) hay độ lệch tiêu chuẩn là một chỉ số quan trọng giúp đo lường mức độ phân tán của một tập dữ liệu quanh giá trị trung bình (Mean). Độ lệch chuẩn không chỉ cho thấy sự dao động trong tập dữ liệu mà còn phản ánh độ ổn định hoặc đa dạng của dữ liệu, điều này rất hữu ích trong nhiều lĩnh vực như nghiên cứu khoa học, kinh doanh và y tế.

Độ lệch chuẩn là gì?

Độ lệch chuẩn đo lường mức độ phân tán của dữ liệu, tức là dữ liệu có thay đổi nhiều hay ít so với giá trị trung bình. Nếu độ lệch chuẩn cao, điều đó có nghĩa là các giá trị trong tập dữ liệu phân tán khá rộng quanh giá trị trung bình. Ngược lại, độ lệch chuẩn thấp cho thấy hầu hết các giá trị trong dữ liệu gần nhau, thể hiện sự ổn định hoặc đồng đều.

Ví dụ, trong một lớp học, nếu điểm số của học sinh có độ lệch chuẩn cao, điều đó có nghĩa là có sự khác biệt rõ rệt giữa các điểm số, một số học sinh rất giỏi nhưng cũng có nhiều học sinh yếu. Nếu độ lệch chuẩn thấp, hầu hết học sinh có điểm số gần như tương đồng.

Độ lệch chuẩn và phương sai

Phương sai là khái niệm cơ bản trong thống kê, đo lường sự phân tán của dữ liệu dưới dạng bình phương của độ lệch. Tuy nhiên, phương sai không dễ hình dung trực quan vì có đơn vị là bình phương của dữ liệu gốc. Để khắc phục điều này, chúng ta sử dụng độ lệch chuẩn, vốn là căn bậc hai của phương sai, giúp đưa giá trị về đơn vị đo lường của dữ liệu gốc.

Mối quan hệ giữa phương sai và độ lệch chuẩn:

Độ lệch chuẩn quần thể và độ lệch chuẩn mẫu

Có hai loại độ lệch chuẩn chính:

• Độ lệch chuẩn quần thể (Population Standard Deviation): Dùng khi bạn có dữ liệu của toàn bộ quần thể. Công thức tính là:

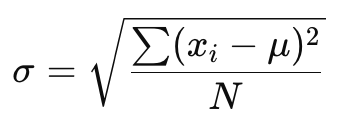
• Độ lệch chuẩn mẫu (Sample Standard Deviation): Dùng khi bạn chỉ có mẫu từ quần thể lớn. Công thức tính là:

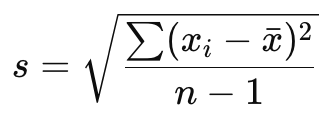
Sự khác biệt giữa hai công thức này là mẫu số. Độ lệch chuẩn mẫu sử dụng $n-1$ thay vì $N$ để bù đắp sai số ước lượng khi lấy mẫu.

Độ lệch chuẩn bao nhiêu là chấp nhận được?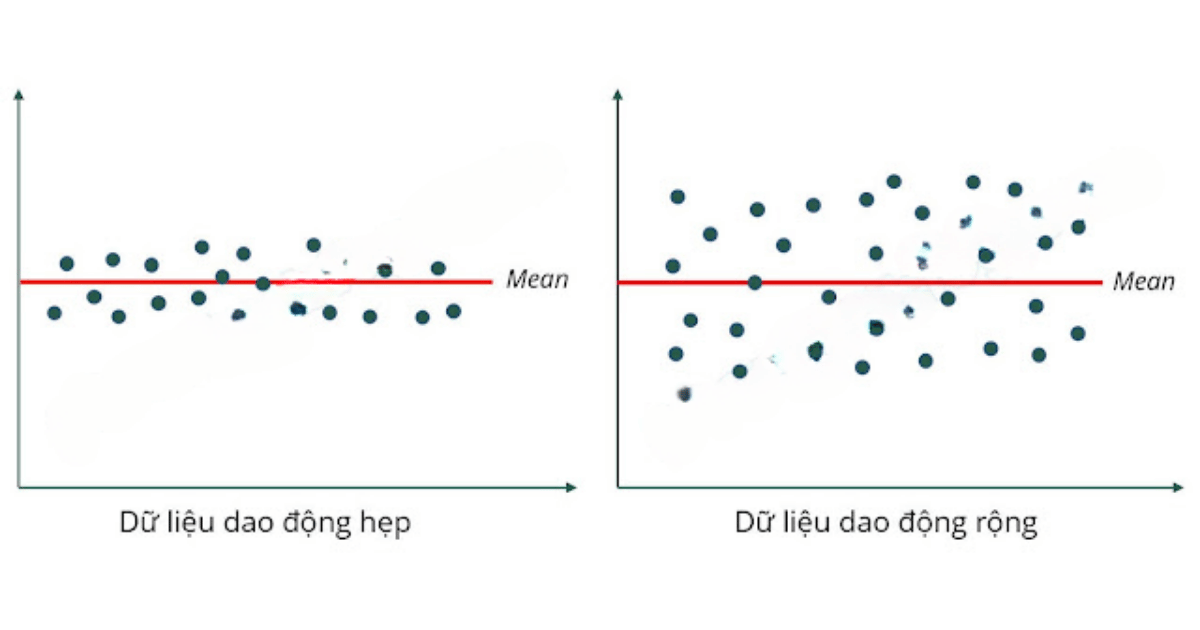

Khi thực hiện thống kê mô tả, người ta thường quan tâm đến độ lệch chuẩn để đánh giá mức độ phân tán của dữ liệu. Tuy nhiên, câu hỏi là độ lệch chuẩn bao nhiêu thì chấp nhận được? thực sự không có một ngưỡng cố định, mà phụ thuộc vào ngữ cảnh nghiên cứu và yêu cầu cụ thể của dữ liệu.

Để đánh giá mức độ biến động của dữ liệu, người ta thường sử dụng hệ số biến động (Coefficient of Variation – CV), được tính bằng công thức:

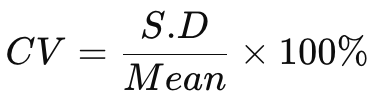
Trong đó:

• S.D: Độ lệch chuẩn
• Mean: Giá trị trung bình của dữ liệu

Phân loại hệ số biến động (CV):

• CV < 10%: thấp (dữ liệu ít biến động)
• 10% ≤ CV < 20%: trung bình
• 20% ≤ CV < 30%: cao
• CV ≥ 30%: rất cao

Ví dụ, trong một lớp học có 50 học sinh, nếu độ lệch chuẩn của điểm môn Toán là 1.112 và giá trị trung bình là 7.65, thì CV = 16.7%, cho thấy mức độ biến động trong điểm số là trung bình.

Độ lệch chuẩn và ứng dụng trong nghiên cứu

• Trong nghiên cứu khoa học: Giúp các nhà nghiên cứu đánh giá mức độ phân tán của các kết quả quan sát. Nếu độ lệch chuẩn thấp, điều này cho thấy các kết quả rất gần nhau, tạo ra kết luận có độ tin cậy cao. Ngược lại, nếu độ lệch chuẩn cao, kết quả có sự phân tán mạnh, điều này có thể chỉ ra sự không ổn định trong dữ liệu hoặc ảnh hưởng của yếu tố ngoài kiểm soát.
• Trong kinh doanh và marketing: Có thể được sử dụng để đánh giá sự đồng nhất của các phản hồi từ khách hàng. Nếu độ lệch chuẩn của các đánh giá về sản phẩm hoặc dịch vụ rất cao, điều này có thể chỉ ra sự bất đồng lớn trong quan điểm khách hàng và yêu cầu doanh nghiệp phải cải thiện chất lượng.
• Trong tài chính: Được sử dụng để đo lường rủi ro đầu tư. Cổ phiếu có độ lệch chuẩn cao thường mang tính rủi ro lớn hơn vì giá cổ phiếu có sự biến động mạnh mẽ.

Đo lường sự phân tán trong nghiên cứu thống kê

Đo lường sự phân tán giúp nhà nghiên cứu hiểu rõ hơn về sự biến động trong dữ liệu. Các công cụ như độ lệch chuẩn và phương sai giúp xác định mức độ dao động của dữ liệu, từ đó đưa ra các quyết định chính xác hơn trong nghiên cứu.

Ứng dụng thực tiễn:

• Trong y tế, nó giúp xác định hiệu quả của phương pháp điều trị hoặc các chương trình y tế. Nếu độ lệch chuẩn của các dữ liệu liên quan đến sức khỏe là thấp, điều này cho thấy sự ổn định trong kết quả điều trị; ngược lại, độ lệch chuẩn cao có thể chỉ ra sự cần thiết phải thay đổi hoặc cải thiện phương pháp điều trị.
• Trong giáo dục, độ lệch chuẩn giúp đánh giá hiệu suất học tập của học sinh. Nếu độ lệch chuẩn cao, có thể thấy rằng học sinh có sự phân bố kết quả rất khác nhau, từ đó giúp giáo viên điều chỉnh phương pháp giảng dạy.

Kết luận

Tóm lại, độ lệch chuẩn và phương sai là các công cụ thống kê quan trọng giúp đo lường sự phân tán trong dữ liệu. Việc hiểu rõ về độ lệch chuẩn, cũng như các ứng dụng và sự khác biệt giữa độ lệch chuẩn quần thể và mẫu, sẽ giúp nhà nghiên cứu và các nhà quản lý có cái nhìn chính xác về sự biến động của dữ liệu. Mặc dù không có một ngưỡng cố định để đánh giá độ lệch chuẩn là “chấp nhận được”, nhưng hiểu biết về cách tính và phân tích độ lệch chuẩn sẽ giúp đưa ra các quyết định tốt hơn trong nhiều lĩnh vực, từ khoa học đến kinh doanh và y tế.