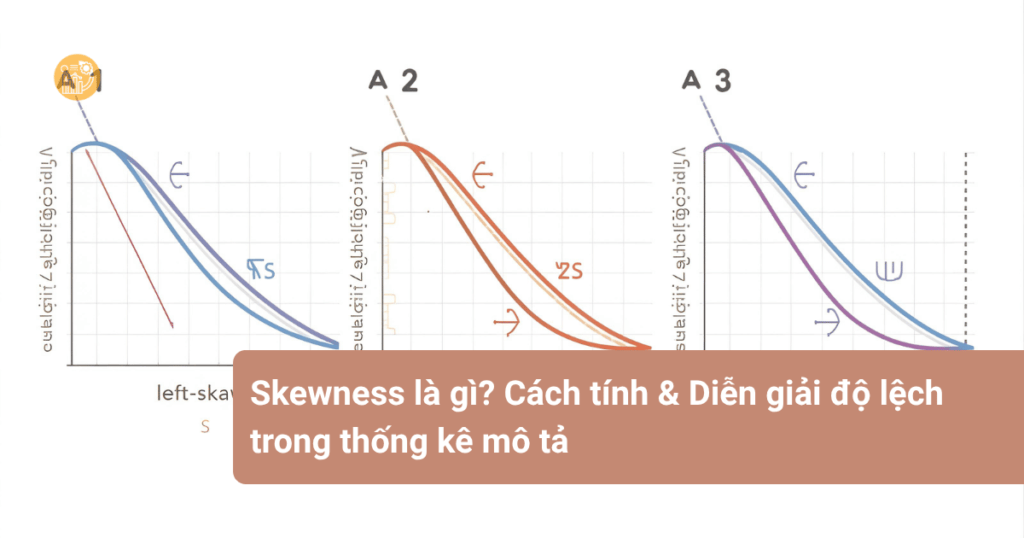
Skewness là gì? Skewness hay còn gọi là độ lệch trong thống kê, là chỉ số cho biết mức độ bất đối xứng của một phân phối dữ liệu so với phân phối chuẩn. Khi dữ liệu có hình chuông hoàn toàn đối xứng, ta nói phân phối đó có skewness = 0. Ngược lại, nếu dữ liệu bị lệch về bên trái hoặc bên phải, skewness sẽ mang giá trị âm hoặc dương.

Trong Xử lý số liệu, việc hiểu rõ skewness là gì giúp người phân tích đánh giá hình dạng của dữ liệu, từ đó chọn mô hình thống kê phù hợp hơn và giải thích ý nghĩa kết quả một cách chính xác.

1. Khái niệm Skewness trong thống kê

Skewness là thước đo cho biết dữ liệu có xu hướng tập trung về phía nào so với trung bình. Khi phân phối bị “kéo dài” về một phía, ta nói dữ liệu bị lệch. Cụ thể:

• Skewness dương (Positive Skewness): Đuôi phân phối kéo dài về bên phải. Giá trị trung bình lớn hơn trung vị. Ví dụ điển hình là phân phối thu nhập, khi một số cá nhân có thu nhập rất cao làm kéo trung bình lên.
• Skewness âm (Negative Skewness): Đuôi phân phối kéo dài về bên trái. Giá trị trung bình nhỏ hơn trung vị. Ví dụ: điểm kiểm tra khi hầu hết học sinh đạt điểm cao, chỉ vài người điểm thấp.
• Skewness bằng 0: Phân phối đối xứng, trung bình bằng trung vị và mode, như phân phối chuẩn.

Trong thực hành, khi bạn biết độ lệch trong thống kê là dương hay âm, bạn sẽ hiểu rõ hơn về xu hướng dữ liệu của mình có đang tập trung nhiều ở giá trị thấp hay cao.

2. Công thức tính Skewness

Skewness có thể được tính theo nhiều cách, trong đó phổ biến nhất là hệ số độ lệch Pearson. Có hai biến thể chính của công thức tính skewness:

Công thức 1: SK1 = (Giá trị trung bình - Yếu vị) / Độ lệch chuẩn
Công thức 2: SK2 = 3 * (Giá trị trung bình - Trung vị) / Độ lệch chuẩn

Trong đó:

• SK1: Hệ số độ lệch thứ nhất của Pearson (Pearson’s Mode Skewness)
• SK2: Hệ số độ lệch thứ hai của Pearson (Pearson’s Median Skewness)
• Độ lệch chuẩn: Đo mức độ phân tán của dữ liệu quanh trung bình

Nếu bạn đang học cách tính skewness trong SPSS, phần mềm sẽ tự động hiển thị giá trị này trong bảng Descriptive Statistics. Việc quan trọng là biết cách đọc kết quả: nếu giá trị skewness nằm trong khoảng -1 đến +1, dữ liệu được coi là khá đối xứng. Nếu vượt quá khoảng này, dữ liệu bị lệch mạnh.

3. Cách đọc Skewness trong SPSS

Khi chạy mô tả trong SPSS (Analyze → Descriptive Statistics → Descriptives), bạn có thể chọn thêm tùy chọn Skewness và Kurtosis. SPSS sẽ hiển thị giá trị skewness kèm theo sai số chuẩn của nó.

Cách đọc skewness trong SPSS:

• Nếu skewness ≈ 0: Dữ liệu đối xứng, gần phân phối chuẩn.
• Nếu skewness > 0: Dữ liệu lệch phải, nhiều giá trị nhỏ, một vài giá trị lớn kéo trung bình lên.
• Nếu skewness < 0: Dữ liệu lệch trái, nhiều giá trị lớn, vài giá trị nhỏ kéo trung bình xuống.

Để dễ nhớ, bạn có thể xem biểu đồ histogram trong SPSS để trực quan hóa: đuôi kéo dài bên nào, skewness sẽ cùng hướng đó.

4. Ví dụ Skewness trong thực tế

Giả sử bạn khảo sát mức thu nhập hàng tháng của 100 người. Kết quả thu được: đa số nằm trong khoảng 10–20 triệu, nhưng có một số cá nhân thu nhập trên 100 triệu. Khi đó, phân phối thu nhập bị lệch phải, nên skewness > 0.

Ngược lại, nếu bạn khảo sát điểm thi và hầu hết học sinh đạt điểm cao (8–10), chỉ vài người điểm thấp (1–3), phân phối sẽ lệch trái, skewness < 0.

Như vậy, qua ví dụ skewness, ta thấy chỉ số này giúp nhà nghiên cứu nhận diện được dạng của phân phối mà không cần nhìn biểu đồ. Điều này đặc biệt hữu ích khi làm việc với dữ liệu lớn trong SPSS hoặc Excel.

5. Ý nghĩa Skewness trong phân phối chuẩn

Hiểu được ý nghĩa skewness trong phân phối chuẩn rất quan trọng vì nhiều mô hình thống kê giả định dữ liệu tuân theo phân phối chuẩn. Nếu dữ liệu có skewness khác 0 quá lớn, các giả định này có thể bị vi phạm.

Ví dụ, trong phân tích hồi quy hoặc kiểm định giả thuyết, dữ liệu lệch nhiều có thể khiến kết quả không còn chính xác. Do đó, trước khi phân tích, các nhà thống kê thường kiểm tra skewness để xem có cần biến đổi dữ liệu (log, square root, hay Box-Cox transformation) nhằm làm giảm độ lệch hay không.

Xử lý số liệu khuyến nghị rằng khi skewness nằm trong khoảng từ -0.5 đến +0.5 thì phân phối có thể xem là chuẩn; nếu vượt ra ngoài khoảng này, cần xem xét điều chỉnh.

6. Tầm quan trọng của Skewness trong phân tích dữ liệu

Biết skewness là gì giúp bạn hiểu sâu hơn về bản chất dữ liệu. Chỉ số này không chỉ mang ý nghĩa mô tả mà còn ảnh hưởng đến độ tin cậy của các phân tích suy luận.

Trong phân tích tài chính, độ lệch trong thống kê thường được dùng để đánh giá rủi ro đầu tư. Nếu lợi nhuận của một cổ phiếu có skewness dương lớn, có nghĩa là khả năng có vài giá trị lợi nhuận cực cao nhưng phần lớn lợi nhuận thấp. Ngược lại, skewness âm thể hiện rủi ro mất mát lớn trong một số ít trường hợp.

7. Tổng kết

Tóm lại, skewness là gì không chỉ là câu hỏi về mặt định nghĩa, mà còn là yếu tố then chốt trong việc hiểu hình dạng và xu hướng của dữ liệu. Biết cách tính skewness, đọc skewness trong SPSS, và diễn giải ý nghĩa skewness trong phân phối chuẩn sẽ giúp bạn đánh giá dữ liệu một cách chuyên nghiệp và chính xác hơn.

Nếu bạn đang học thống kê hoặc làm việc trong lĩnh vực Xử lý số liệu, hãy luôn kiểm tra skewness cùng với kurtosis để hiểu rõ hơn về đặc trưng của tập dữ liệu trước khi ra quyết định hoặc chạy mô hình dự đoán.

Bài viết được biên soạn độc quyền bởi xulysolieu.info, chuyên trang phân tích dữ liệu và xử lý số liệu học thuật.