Mô hình OLS (Ordinary Least Squares) là nền tảng quan trọng nhất của phân tích hồi quy trong kinh tế lượng và thống kê ứng dụng. Hầu hết các phương pháp phân tích định lượng nâng cao đều bắt nguồn từ hoặc mở rộng dựa trên mô hình OLS. Vì vậy, việc hiểu đúng bản chất, giả định và cách diễn giải kết quả của mô hình này là yêu cầu bắt buộc đối với người làm nghiên cứu khoa học và phân tích dữ liệu.

Bài viết này trình bày một cách hệ thống về mô hình OLS, từ định nghĩa, công thức, giả định mô hình, quy trình ước lượng cho đến các ứng dụng thực tiễn trong hồi quy tuyến tính.

1. Mô hình OLS là gì?

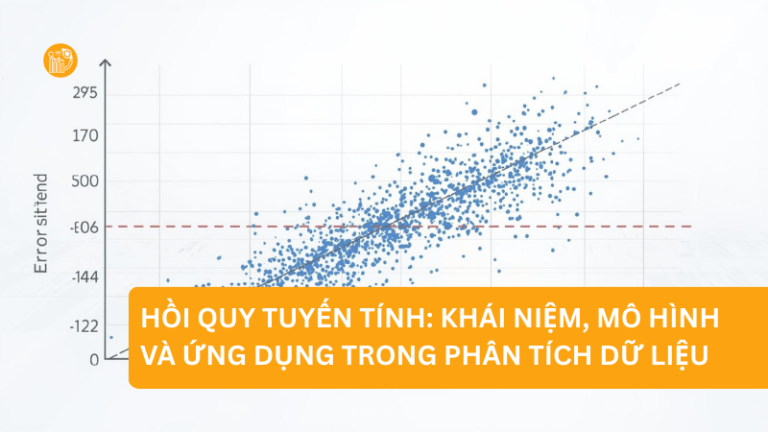
Mô hình OLS là phương pháp ước lượng các tham số của mô hình hồi quy tuyến tính bằng cách tối thiểu hóa tổng bình phương sai số hồi quy giữa giá trị quan sát và giá trị dự đoán. Nói cách khác, OLS tìm ra đường thẳng (hoặc siêu phẳng trong trường hợp nhiều biến) phù hợp nhất với dữ liệu.

Trong tiếng Anh, mô hình OLS được gọi là Ordinary Least Squares, nhấn mạnh nguyên lý “bình phương tối thiểu”.

2. Công thức toán học của mô hình OLS

Với hồi quy tuyến tính đơn giản, mô hình OLS được biểu diễn như sau:

Y_i = β₀ + β₁X_i + ε_i

Trong đó:

• Y_i: biến phụ thuộc tại quan sát i
• X_i: biến độc lập
• β₀: hằng số (intercept)
• β₁: hệ số hồi quy
• ε_i: sai số hồi quy

Mục tiêu của ước lượng OLS là tìm các giá trị β̂₀ và β̂₁ sao cho:

∑(Y_i − Ŷ_i)² là nhỏ nhất

Đây chính là bản chất cốt lõi của mô hình OLS.

3. Ý nghĩa của sai số hồi quy trong mô hình OLS

Trong thực tế, biến độc lập không thể giải thích hoàn toàn biến phụ thuộc. Phần chênh lệch giữa giá trị thực tế và giá trị dự đoán được gọi là sai số hồi quy.

Trong mô hình OLS, sai số hồi quy đại diện cho:

• Các yếu tố bị bỏ sót
• Sai số đo lường
• Biến động ngẫu nhiên

Việc xử lý và kiểm soát sai số hồi quy là điều kiện quan trọng để mô hình có ý nghĩa thống kê.

4. Các giả định mô hình OLS

Để ước lượng OLS có tính không chệch và hiệu quả, giả định mô hình sau cần được thỏa mãn:

4.1. Tuyến tính

Mối quan hệ giữa biến phụ thuộc và biến độc lập phải tuyến tính theo tham số.

4.2. Kỳ vọng sai số bằng 0

E(ε_i) = 0, đảm bảo mô hình không bị chệch.

4.3. Đồng nhất phương sai

Phương sai của sai số hồi quy là không đổi (homoscedasticity).

4.4. Không tự tương quan

Sai số hồi quy của các quan sát phải độc lập với nhau.

4.5. Không đa cộng tuyến hoàn hảo

Các biến độc lập không được có quan hệ tuyến tính hoàn hảo.

Nếu các giả định mô hình bị vi phạm, kết quả của mô hình OLS có thể không còn đáng tin cậy.

5. Quy trình ước lượng OLS

Một quy trình ước lượng OLS chuẩn thường gồm các bước:

1. Thu thập và làm sạch dữ liệu
2. Xác định dạng mô hình hồi quy tuyến tính
3. Ước lượng hệ số bằng phương pháp OLS
4. Kiểm định các giả định mô hình
5. Diễn giải kết quả

Quy trình này được áp dụng xuyên suốt trong các phần mềm thống kê như SPSS, Stata, R.

6. Mô hình OLS dạng log-log

Một biến thể phổ biến của mô hình OLS là dạng log-log, trong đó cả biến phụ thuộc và biến độc lập đều được logarit hóa:

ln(Y_i) = β₀ + β₁ln(X_i) + ε_i

Trong mô hình này, hệ số β₁ được hiểu là độ co giãn (elasticity), tức là Y thay đổi bao nhiêu phần trăm khi X thay đổi 1%.

Dạng log-log giúp mô hình OLS phù hợp hơn với các mối quan hệ tỷ lệ và giảm hiện tượng phương sai thay đổi.

7. Ứng dụng của mô hình OLS

Mô hình OLS được sử dụng rộng rãi trong nhiều lĩnh vực:

• Kinh tế học: phân tích tiêu dùng, thu nhập, GDP
• Tài chính: đánh giá tác động của lãi suất, rủi ro
• Xã hội học: nghiên cứu giáo dục, thu nhập, hành vi
• Kinh doanh: phân tích doanh thu, quảng cáo

Nhờ tính đơn giản và khả năng diễn giải rõ ràng, mô hình OLS luôn là lựa chọn đầu tiên trong phân tích hồi quy.

8. Ưu điểm và hạn chế của mô hình OLS

Ưu điểm

• Dễ ước lượng và dễ diễn giải
• Nền tảng cho nhiều mô hình nâng cao
• Phù hợp với dữ liệu định lượng

Hạn chế

• Nhạy cảm với ngoại lệ
• Phụ thuộc mạnh vào giả định mô hình
• Không phù hợp với quan hệ phi tuyến phức tạp

9. Kết luận

Mô hình OLS là công cụ cốt lõi trong hồi quy tuyến tính và phân tích dữ liệu định lượng. Việc hiểu rõ ordinary least squares, ước lượng OLS, giả định mô hình và sai số hồi quy giúp người nghiên cứu sử dụng mô hình đúng cách và đưa ra kết luận đáng tin cậy.

Nếu bạn cần hỗ trợ học tập, chạy hồi quy hoặc Xử lý số liệu chuyên sâu, có thể tham khảo tại: