Trong phân tích dữ liệu định lượng, khi mục tiêu không chỉ dừng lại ở việc so sánh hai nhóm mà là so sánh trung bình của từ ba nhóm trở lên, phương pháp được sử dụng phổ biến nhất chính là phân tích phương sai một yếu tố. Đây là kỹ thuật thống kê nền tảng, xuất hiện rất nhiều trong nghiên cứu kinh tế, marketing, giáo dục, xã hội học và khoa học hành vi. Bài viết này sẽ giúp bạn hiểu rõ bản chất, điều kiện áp dụng, cách thực hiện và cách diễn giải kết quả phân tích phương sai một yếu tố theo hướng dễ hiểu, đúng logic thống kê và phù hợp khi làm việc với SPSS.

Phân tích phương sai một yếu tố là gì?

Phân tích phương sai một yếu tố (còn gọi là one way anova) là phương pháp kiểm định thống kê dùng để đánh giá sự khác biệt về giá trị trung bình của một biến định lượng giữa nhiều nhóm độc lập được phân loại theo một biến định tính.

Hiểu một cách đơn giản, phân tích phương sai một yếu tố trả lời cho câu hỏi: trung bình của các nhóm có bằng nhau hay không, và sự khác biệt quan sát được có đủ lớn để không phải do ngẫu nhiên hay không.

Ví dụ điển hình của phân tích phương sai một yếu tố là so sánh mức độ hài lòng trung bình giữa các nhóm tuổi, các nhóm thu nhập hoặc các nhóm nghề nghiệp đối với cùng một sản phẩm hay dịch vụ.

Khi nào nên sử dụng phân tích phương sai 1 yếu tố?

Bạn nên sử dụng phân tích phương sai 1 yếu tố trong các trường hợp sau:

• Biến phụ thuộc là biến định lượng (ví dụ: điểm số, mức độ hài lòng, doanh thu, thời gian).
• Biến độc lập là một biến phân loại có từ hai nhóm trở lên.
• Mục tiêu là so sánh trung bình nhiều nhóm thay vì chỉ hai nhóm.

Nếu chỉ có hai nhóm, kết quả phân tích phương sai 1 yếu tố về mặt bản chất sẽ tương đương với kiểm định t-test độc lập. Tuy nhiên, khi số nhóm tăng lên, anova là lựa chọn bắt buộc để tránh sai lầm thống kê.

Bản chất thống kê của one way anova

Về nguyên lý, one way anova không so sánh trực tiếp từng cặp trung bình với nhau mà so sánh mức độ biến thiên giữa các nhóm với mức độ biến thiên trong nội bộ từng nhóm.

Chỉ số trung tâm của kiểm định anova là f-statistic. Chỉ số này được tính bằng tỷ lệ giữa phương sai giữa các nhóm và phương sai trong các nhóm. Nếu sự khác biệt giữa các nhóm đủ lớn so với sự dao động bên trong từng nhóm, giá trị f-statistic sẽ lớn và dẫn đến kết quả có ý nghĩa thống kê.

Giả thuyết trong kiểm định anova

Khi thực hiện phân tích phương sai 1 yếu tố, ta luôn xây dựng hai giả thuyết:

• Giả thuyết H₀: Trung bình của các nhóm bằng nhau.
• Giả thuyết H₁: Có ít nhất một nhóm có trung bình khác với các nhóm còn lại.

Mục tiêu của kiểm định anova là sử dụng dữ liệu mẫu để quyết định có đủ bằng chứng bác bỏ H₀ hay không.

Các giả định cần thỏa mãn trong phân tích phương sai 1 yếu tố

Để kết quả phân tích phương sai 1 yếu tố đáng tin cậy, dữ liệu cần đáp ứng một số giả định quan trọng:

• Các nhóm so sánh phải độc lập và được chọn ngẫu nhiên.
• Biến phụ thuộc trong mỗi nhóm có phân phối chuẩn hoặc cỡ mẫu đủ lớn để tiệm cận chuẩn.
• Phương sai của các nhóm phải đồng nhất.

Trong trường hợp giả định về phân phối chuẩn hoặc phương sai đồng nhất không thỏa mãn, bạn có thể cân nhắc sử dụng kiểm định phi tham số như Kruskal-Wallis để thay thế cho kiểm định anova.

Thực hiện phân tích phương sai 1 yếu tố trong SPSS

Để thực hành phân tích phương sai 1 yếu tố trong SPSS, bạn thực hiện theo các bước cơ bản sau:

• Vào menu Analyze → Compare Means → One-Way ANOVA.

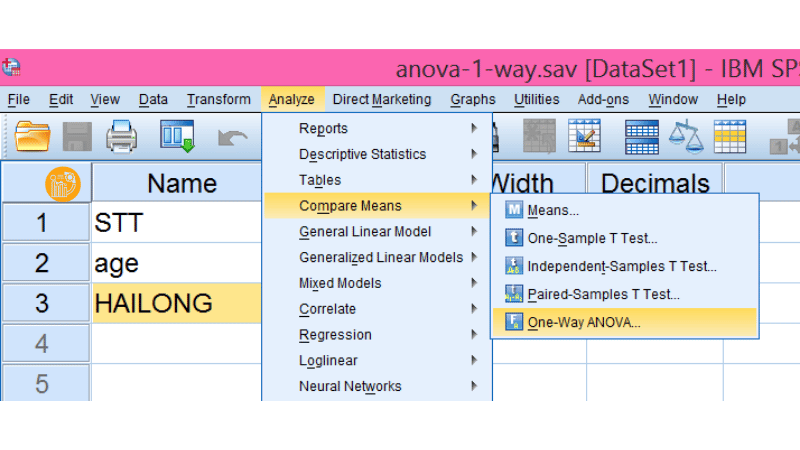
• Đưa biến phụ thuộc vào ô Dependent List.

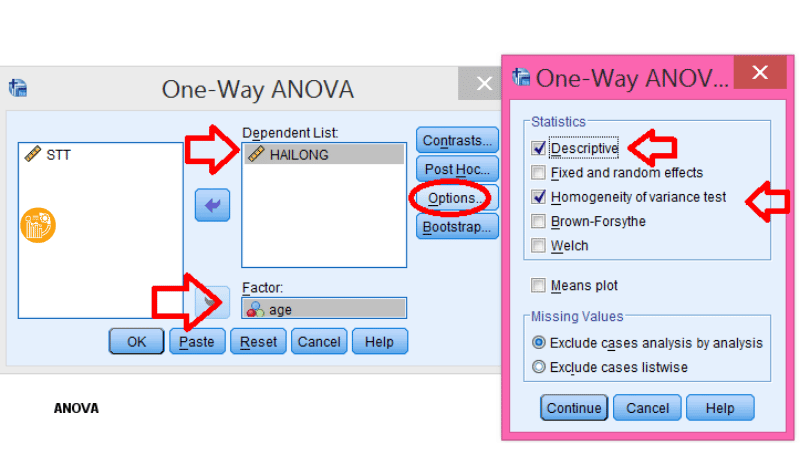
• Đưa biến phân nhóm vào ô Factor.

Đây là thao tác chuẩn khi thực hiện one way anova trong SPSS cho bài toán so sánh trung bình nhiều nhóm.

Kiểm định phương sai đồng nhất

Trước khi diễn giải kết quả chính của kiểm định anova, bạn cần kiểm tra giả định phương sai đồng nhất thông qua kiểm định Levene.

Giả thuyết của Levene test là: phương sai của các nhóm bằng nhau. Cách diễn giải như sau:

• Nếu Sig ≤ 0.05: bác bỏ giả thuyết phương sai bằng nhau, chưa đủ điều kiện để tin cậy kết quả anova.
• Nếu Sig > 0.05: chấp nhận giả thuyết phương sai bằng nhau, có thể tiếp tục phân tích anova.

Việc kiểm tra này là bước không thể bỏ qua trong phân tích phương sai 1 yếu tố.

Diễn giải bảng ANOVA

Bảng ANOVA là bảng quan trọng nhất trong kiểm định anova. Trong bảng này, bạn cần chú ý đến giá trị Sig (p-value).

• Nếu Sig ≤ 0.05: bác bỏ H₀, kết luận có sự khác biệt về trung bình giữa các nhóm.
• Nếu Sig > 0.05: chấp nhận H₀, chưa đủ bằng chứng để kết luận có sự khác biệt.

Ví dụ: nếu Sig = 0.827, điều này cho thấy chưa đủ cơ sở thống kê để khẳng định trung bình giữa các nhóm là khác nhau. Trong trường hợp này, phân tích phương sai 1 yếu tố cho kết luận rằng sự khác biệt quan sát được có thể do ngẫu nhiên.

Vai trò của f-statistic trong kiểm định anova

F-statistic phản ánh mức độ chênh lệch giữa các nhóm so với mức độ biến thiên bên trong từng nhóm. Giá trị f càng lớn thì khả năng tồn tại sự khác biệt thật sự giữa các nhóm càng cao.

Tuy nhiên, trong thực hành, người phân tích thường dựa trực tiếp vào p-value đi kèm f-statistic để đưa ra kết luận thay vì tự so sánh giá trị f.

Phân tích sâu sau ANOVA (Post-hoc)

Khi kết quả phân tích phương sai 1 yếu tố cho thấy có sự khác biệt có ý nghĩa thống kê, câu hỏi tiếp theo là: sự khác biệt nằm giữa những nhóm nào?

Lúc này, các kiểm định hậu nghiệm (post-hoc) như Tukey, LSD, Bonferroni, Duncan sẽ được sử dụng để so sánh từng cặp nhóm cụ thể. Đây là bước phân tích sâu giúp giải thích rõ hơn kết quả kiểm định anova.

Nếu biến phân nhóm chỉ có hai nhóm, phân tích post-hoc không cần thiết vì kết quả anova đã đủ để kết luận.

Ý nghĩa thực tiễn của phân tích phương sai 1 yếu tố

Phân tích phương sai 1 yếu tố không chỉ mang ý nghĩa thống kê mà còn có giá trị ứng dụng rất lớn. Trong marketing, nó giúp so sánh mức độ hài lòng giữa các phân khúc khách hàng. Trong giáo dục, nó hỗ trợ đánh giá kết quả học tập giữa các nhóm sinh viên. Trong quản trị, nó giúp ra quyết định dựa trên sự khác biệt trung bình giữa các nhóm đối tượng.

Tuy nhiên, cần lưu ý rằng kiểm định anova chỉ cho biết có sự khác biệt hay không, chứ không giải thích nguyên nhân của sự khác biệt đó.

Hỗ trợ phân tích và xử lý số liệu

Nếu bạn gặp khó khăn trong việc thực hiện phân tích phương sai 1 yếu tố, diễn giải bảng kết quả hoặc lựa chọn kiểm định phù hợp, bạn có thể tham khảo dịch vụ tại [xulysolieu.info](https://xulysolieu.info/) – Xử lý số liệu. Đội ngũ hỗ trợ tập trung vào việc giải thích bản chất thống kê, giúp bạn hiểu và tự áp dụng vào nghiên cứu thực tế.

Liên hệ: 0878968468

Kết luận

Phân tích phương sai 1 yếu tố là công cụ cốt lõi để so sánh trung bình nhiều nhóm trong nghiên cứu định lượng. Thông qua one way anova, f-statistic và kiểm định anova, nhà nghiên cứu có thể đưa ra kết luận khách quan về sự khác biệt giữa các nhóm. Khi được áp dụng đúng giả định và diễn giải cẩn trọng, phân tích phương sai 1 yếu tố sẽ giúp nâng cao độ tin cậy và giá trị khoa học của nghiên cứu.