Bộ tài liệu hướng dẫn guideline hỗ trợ khóa luận tốt nghiệp & luận văn
Đối với hầu hết sinh viên năm cuối, khóa luận tốt nghiệp hay luận văn thạc sĩ là giai đoạn vừa quan trọng vừa đầy áp lực. Đây không chỉ là bài kiểm tra cuối cùng đánh giá năng lực học thuật mà còn là bước đệm giúp sinh viên rèn luyện tư duy nghiên cứu, kỹ năng phân tích và khả năng viết khoa học. Tuy nhiên, thực tế cho thấy phần lớn sinh viên gặp rất nhiều khó khăn trong quá trình thực hiện đề tài của mình.
Nhiều bạn bắt đầu với sự mơ hồ về quy trình nghiên cứu: không biết nên chọn đề tài như thế nào cho phù hợp, không rõ nên sử dụng phương pháp định tính hay định lượng, và càng lúng túng hơn khi phải thiết kế bảng hỏi, xử lý dữ liệu hoặc trình bày kết quả. Một số bạn khác lại mất quá nhiều thời gian tra cứu tài liệu, hoặc làm theo các “mẫu có sẵn” trên mạng mà không hiểu bản chất, dẫn đến sai quy trình, thiếu tính khoa học, và bị trừ điểm đáng tiếc trong quá trình bảo vệ.
Chính từ những vướng mắc thực tế đó, Xử Lý Số Liệu (Xulysolieu.info) đã phát triển và tổng hợp bộ tài liệu hướng dẫn chuẩn khoa học, được thiết kế chuyên biệt dành cho sinh viên và học viên đang thực hiện đề tài nghiên cứu. Bộ tài liệu này đóng vai trò như một “bản đồ nghiên cứu” chi tiết, giúp bạn nắm bắt toàn bộ quy trình — từ việc xác định đề tài, thiết kế bảng hỏi, đến phân tích dữ liệu bằng SPSS, AMOS, SmartPLS và trình bày báo cáo hoàn chỉnh.
Với bộ tài liệu hướng dẫn của Xử Lý Số Liệu, sinh viên không chỉ rút ngắn thời gian làm khóa luận, mà còn học được cách tư duy khoa học, làm việc có hệ thống và tự tin bảo vệ kết quả nghiên cứu của mình.
Tài liệu hướng dẫn là gì?
Khi nhắc đến “tài liệu hướng dẫn”, nhiều sinh viên thường nghĩ đơn giản rằng đó chỉ là một tập file PDF chứa các mẫu đề cương, bảng hỏi hoặc gợi ý trình bày khóa luận. Tuy nhiên, trong môi trường học thuật, khái niệm này mang ý nghĩa sâu rộng hơn nhiều.
“Tài liệu hướng dẫn” là một hệ thống tổng hợp các hướng dẫn, mẫu biểu và gợi ý phương pháp nghiên cứu được xây dựng dựa trên chuẩn mực khoa học. Nó giúp người học hiểu rõ cách thực hiện từng bước trong quá trình làm khóa luận hoặc luận văn, từ khâu chọn đề tài, thiết kế mô hình nghiên cứu, thu thập dữ liệu, cho đến phân tích và trình bày kết quả.
Khác với việc chỉ “làm theo cảm tính” hay “copy mẫu có sẵn”, tài liệu hướng dẫn chuẩn khoa học giúp sinh viên nắm được bản chất của từng thao tác, hiểu vì sao phải làm chứ không chỉ làm thế nào. Điều này giúp bạn chủ động hơn, giảm sai sót và đặc biệt là rút ngắn đáng kể thời gian học hỏi.

Vai trò của tài liệu hướng dẫn trong nghiên cứu
- Giúp định hình tư duy nghiên cứu có hệ thống, tránh lan man hoặc bỏ sót bước quan trọng.
- Cung cấp mẫu biểu, biểu mẫu, và ví dụ minh họa giúp sinh viên dễ hình dung và áp dụng.
- Hỗ trợ trình bày bài khóa luận đúng chuẩn, hạn chế lỗi định dạng, trích dẫn hoặc sai kỹ thuật khi xử lý dữ liệu.
So sánh giữa “tài liệu hướng dẫn chuẩn học thuật” và “tài liệu chia sẻ kinh nghiệm cá nhân”
| Tiêu chí | Tài liệu hướng dẫn chuẩn học thuật | Tài liệu chia sẻ kinh nghiệm cá nhân |
| Cơ sở xây dựng | Dựa trên quy trình nghiên cứu khoa học, có trích dẫn lý thuyết và chuẩn mực học thuật | Dựa vào trải nghiệm chủ quan của cá nhân |
| Mục tiêu | Hỗ trợ người học thực hiện nghiên cứu đúng quy trình và có cơ sở khoa học | Truyền cảm hứng, chia sẻ mẹo làm nhanh, mẹo viết bài |
| Giá trị ứng dụng | Cao, có thể sử dụng trong mọi đề tài và ngành học | Hạn chế, chỉ phù hợp với một số trường hợp cụ thể |
| Tính cập nhật | Được biên soạn, kiểm chứng và điều chỉnh theo chuẩn mới | Thường không được cập nhật thường xuyên |
| Ví dụ điển hình | Bộ tài liệu hướng dẫn của Xử Lý Số Liệu (Xulysolieu.info) | Các bài chia sẻ kinh nghiệm cá nhân trên diễn đàn, nhóm Facebook |
Những khó khăn thường gặp khi làm khóa luận, luận văn
Thực hiện một khóa luận tốt nghiệp hay luận văn thạc sĩ là một quá trình đòi hỏi tư duy hệ thống, kỹ năng nghiên cứu và sự kiên trì cao. Tuy nhiên, phần lớn sinh viên và học viên khi bắt tay vào làm đề tài đều gặp phải nhiều trở ngại, đặc biệt là khi chưa có tài liệu hướng dẫn cụ thể và rõ ràng.
Không biết cách chọn đề tài và xây dựng mô hình nghiên cứu
Đây là khó khăn đầu tiên và phổ biến nhất. Nhiều sinh viên bối rối không biết chọn đề tài nào vừa phù hợp với chuyên ngành, vừa có tính thực tiễn và khả thi về mặt dữ liệu. Sau khi chọn đề tài, việc xây dựng mô hình nghiên cứu và giả thuyết khoa học lại càng trở nên khó khăn hơn — bởi không hiểu rõ mối quan hệ giữa các biến hoặc cách diễn đạt giả thuyết đúng chuẩn học thuật.
Không hiểu rõ sự khác biệt giữa phương pháp định tính và định lượng
Phần lớn sinh viên mới tiếp cận nghiên cứu chỉ nắm khái niệm mơ hồ về hai phương pháp này. Họ không biết khi nào nên dùng phỏng vấn chuyên sâu (định tính) và khi nào cần sử dụng khảo sát bảng hỏi, phân tích số liệu (định lượng). Việc thiếu hiểu biết về phương pháp dễ khiến nghiên cứu sai hướng, mất tính logic và khó đạt được độ tin cậy.
Khó khăn khi phân tích dữ liệu bằng phần mềm SPSS, AMOS, SmartPLS
Phân tích dữ liệu là giai đoạn khiến nhiều sinh viên “chùn bước” nhất. Việc sử dụng các phần mềm như SPSS để chạy thống kê mô tả, AMOS để kiểm định mô hình cấu trúc (SEM) hay SmartPLS để đánh giá biến bậc hai… đòi hỏi kiến thức vững và khả năng đọc hiểu kết quả. Thiếu hướng dẫn cụ thể, nhiều sinh viên không biết bắt đầu từ đâu hoặc không hiểu cách diễn giải kết quả một cách chính xác.
Thiếu mẫu trình bày và hướng dẫn viết phần kết quả, thảo luận
Ngay cả khi đã có kết quả phân tích, nhiều sinh viên vẫn gặp khó khăn trong khâu trình bày và viết báo cáo khóa luận. Không ít bài bị trừ điểm vì lỗi định dạng, bảng biểu không thống nhất, hoặc phần thảo luận thiếu tính kết nối với mô hình nghiên cứu. Việc không có mẫu trình bày chuẩn khiến bài làm thiếu tính khoa học và thẩm mỹ học thuật.
Bộ tài liệu hướng dẫn từ Xử Lý Số Liệu gồm những gì?
Phần 1 – Định hướng nghiên cứu
- Cách chọn đề tài phù hợp, xây dựng mục tiêu, câu hỏi và giả thuyết.
- Mẫu khung đề cương chuẩn theo quy định các trường đại học.
Phần 2 – Thiết kế bảng hỏi và thu thập dữ liệu
- Hướng dẫn tạo bảng hỏi với thang đo Likert, cách mã hóa dữ liệu.
- Mẹo tránh sai lệch trong khảo sát và cách làm sạch dữ liệu trước khi nhập SPSS.
Phần 3 – Phân tích dữ liệu
- Hướng dẫn chạy các phần mềm nghiên cứu khoa học SPSS, AMOS, SMARTPLS, STATA, EVIEWS,…
- Cách đọc kết quả và viết phần “Kết quả nghiên cứu” đúng chuẩn.
- Mẫu bảng biểu, biểu đồ minh họa có thể chèn trực tiếp vào khóa luận.
Phần 4 – Trình bày & Hoàn thiện báo cáo
- Format chuẩn: canh lề, font, bố cục, bảng biểu.
- Hướng dẫn trích dẫn tài liệu tham khảo theo chuẩn APA/Harvard.
- Checklist hoàn thiện bài trước khi nộp hoặc bảo vệ.
Lợi ích khi sử dụng bộ tài liệu hướng dẫn này
Tiết kiệm thời gian học và tra cứu
Bạn không cần mất công tìm kiếm hàng chục nguồn tài liệu khác nhau hay xem các video hướng dẫn rời rạc. Tất cả nội dung – từ cách chọn đề tài, thiết kế bảng hỏi, đến phân tích dữ liệu và trình bày kết quả – đều được hệ thống hóa rõ ràng trong một bộ tài liệu duy nhất.
Có hệ thống – tuần tự từng bước
Bộ tài liệu được xây dựng theo đúng quy trình nghiên cứu khoa học chuẩn quốc tế, chia nhỏ thành từng giai đoạn cụ thể: từ “hình thành ý tưởng” → “thu thập dữ liệu” → “phân tích kết quả” → “hoàn thiện báo cáo”. Nhờ đó, người học dễ dàng làm theo và không bỏ sót bước nào quan trọng.
Dễ áp dụng cho mọi đề tài, mọi chuyên ngành
Dù bạn học kinh tế, quản trị, tâm lý học, giáo dục hay công nghệ, bộ tài liệu hướng dẫn vẫn có thể áp dụng linh hoạt. Mỗi phần đều có mẫu minh họa và ví dụ thực tế để bạn tùy chỉnh cho phù hợp với đề tài riêng, giúp khóa luận của bạn mang tính cá nhân hóa mà vẫn đảm bảo tính học thuật.
Đảm bảo bài làm đạt chuẩn khoa học và dễ bảo vệ
Các hướng dẫn trong bộ tài liệu đều dựa trên chuẩn đánh giá của hội đồng khoa học và các trường đại học hàng đầu, giúp bạn biết chính xác cách trình bày, cách diễn giải kết quả và cách phản biện khi bảo vệ. Nhờ đó, bài khóa luận hoặc luận văn của bạn sẽ được đánh giá cao cả về nội dung lẫn hình thức.
Ai nên sử dụng bộ tài liệu hướng dẫn này?
Bộ tài liệu hướng dẫn do Xử Lý Số Liệu (Xulysolieu.info) biên soạn không chỉ dành riêng cho một nhóm người học cụ thể, mà được thiết kế để phù hợp với nhiều đối tượng khác nhau trong môi trường nghiên cứu và học thuật. Dưới đây là những nhóm người có thể khai thác tối đa giá trị của bộ tài liệu này:
Sinh viên năm cuối đang làm khóa luận tốt nghiệp
Đây là nhóm đối tượng chính mà bộ tài liệu hướng dẫn hướng đến. Với sinh viên năm cuối, khóa luận thường là thử thách lớn nhất trong hành trình đại học — nơi đòi hỏi sự kết hợp giữa kiến thức lý thuyết và kỹ năng thực hành nghiên cứu. Bộ tài liệu giúp sinh viên:
- Biết cách chọn đề tài phù hợp với ngành học và xu hướng xã hội.
- Hiểu quy trình nghiên cứu chuẩn, tránh sai sót về phương pháp và trình bày.
- Tự tin hơn trong việc phân tích dữ liệu bằng SPSS, AMOS, SmartPLS và viết phần kết quả thuyết phục.
Học viên cao học đang thực hiện luận văn
Đối với học viên cao học, luận văn không chỉ đòi hỏi sự chính xác về kỹ thuật mà còn cần tính mới, tính học thuật và khả năng đóng góp thực tiễn. Bộ tài liệu hướng dẫn của Xử Lý Số Liệu giúp học viên:
- Nắm vững cấu trúc một luận văn đạt chuẩn (theoretical framework, hypothesis, discussion, implications…).
- Thành thạo các kỹ thuật phân tích dữ liệu nâng cao, đảm bảo kết quả có độ tin cậy cao.
- Tiết kiệm thời gian tự học và giảm sai sót trong giai đoạn hoàn thiện.
Người làm nghiên cứu, giảng viên và trợ giảng
Không chỉ sinh viên hay học viên, người làm nghiên cứu và giảng viên hướng dẫn khóa luận cũng có thể sử dụng bộ tài liệu này như một tài liệu tham khảo hệ thống để:
- Cập nhật quy trình nghiên cứu mới nhất phù hợp với chuẩn quốc tế.
- Hướng dẫn sinh viên thực hiện đề tài một cách khoa học và dễ hiểu hơn.
- Sử dụng các mẫu bảng hỏi, biểu mẫu, cấu trúc báo cáo có sẵn để tiết kiệm thời gian hướng dẫn.
Cảm nhận của người dùng
“Trước đây mình không biết bắt đầu từ đâu khi làm khóa luận, nhưng nhờ tài liệu hướng dẫn của Xử Lý Số Liệu, mình nắm được toàn bộ quy trình từ A–Z.” – Ngọc Lan, sinh viên Đại học Kinh tế TP.HCM
“Bộ guideline giúp mình tiết kiệm ít nhất 2 tuần trong quá trình xử lý dữ liệu. Tất cả đều được hướng dẫn chi tiết và dễ hiểu, đặc biệt là phần Cronbach’s Alpha và EFA.” – Minh Hoàng, học viên cao học UEH
“Trước khi biết đến Xử Lý Số Liệu, mình cứ loay hoay mãi với phần phân tích SEM và không biết diễn giải kết quả thế nào. Nhờ bộ tài liệu hướng dẫn, mình hiểu rõ từng bước và tự tin viết phần thảo luận khoa học hơn.” – Thùy Trang, sinh viên Đại học Ngoại thương (FTU)
Trong hành trình hoàn thiện khóa luận tốt nghiệp hay luận văn thạc sĩ, việc có trong tay một bộ tài liệu hướng dẫn chuẩn khoa học chính là lợi thế lớn giúp sinh viên tiết kiệm thời gian, định hướng rõ ràng và tránh sai sót trong quá trình nghiên cứu.
Bộ tài liệu hướng dẫn của Xử Lý Số Liệu (Xulysolieu.info) không chỉ đơn thuần là tập hợp các biểu mẫu và quy trình kỹ thuật, mà còn là một người đồng hành đáng tin cậy — giúp bạn hiểu bản chất của từng bước nghiên cứu, áp dụng đúng phương pháp và trình bày bài làm đạt chuẩn học thuật.
Dù bạn là sinh viên năm cuối, học viên cao học, hay giảng viên đang hướng dẫn nghiên cứu, bộ tài liệu này đều mang lại giá trị thực tiễn và học thuật vượt trội, giúp quá trình nghiên cứu trở nên đơn giản, logic và tự tin hơn bao giờ hết.
🎓 Bắt đầu ngay hôm nay!
👉 Truy cập ngay bộ “Tài liệu hướng dẫn hoàn thiện khóa luận & luận văn” miễn phí tại: 🔗 http://tiny.cc/xlslguideline
👉 Hoặc liên hệ trực tiếp Xử Lý Số Liệu để được tư vấn miễn phí cách sử dụng tài liệu và hỗ trợ phân tích dữ liệu bằng SPSS, AMOS, SmartPLS.
Phân tích hồi quy tuyến tính bội trong SPSS: Cách chạy & Đọc kết quả chi tiết
Hồi quy tuyến tính bội là gì?
Hồi quy tuyến tính bội (Multiple Linear Regression – MLR) là mô hình thống kê được sử dụng để mô tả mối quan hệ giữa một biến phụ thuộc và nhiều biến độc lập thông qua một phương trình tuyến tính. Mô hình này giúp xác định mức độ ảnh hưởng của các yếu tố độc lập đến biến phụ thuộc và có thể dự báo giá trị của biến phụ thuộc dựa trên các giá trị của các biến độc lập.
Phương trình hồi quy tuyến tính bội có dạng:
Y = β₀ + β₁X₁ + β₂X₂ + ... + βnXn + ε
Trong đó:
- Y: Biến phụ thuộc (biến cần dự đoán).
- X₁, X₂, …, Xn: Các biến độc lập.
- β₀: Hằng số hồi quy (intercept).
- β₁, β₂, …, βn: Các hệ số hồi quy (slope).
- ε: Phần dư (residuals).
Các bước thực hiện phân tích hồi quy tuyến tính bội trong SPSS
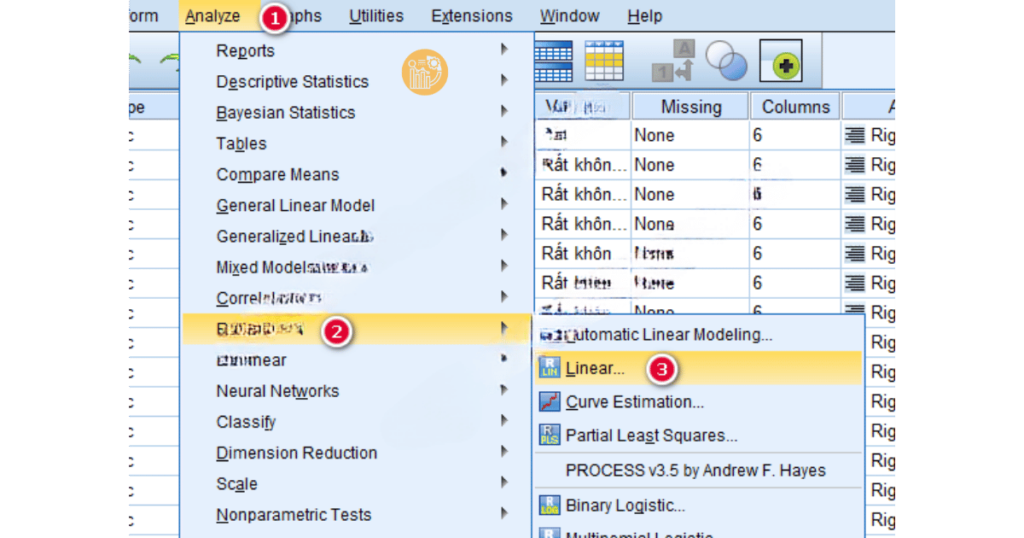
B1: Chọn phương pháp hồi quy trong SPSS: Để bắt đầu phân tích hồi quy tuyến tính bội trong SPSS, bạn vào menu Analyze > Regression > Linear. Sau đó, nhập biến phụ thuộc vào ô “Dependent” và các biến độc lập vào ô “Independent(s)”.
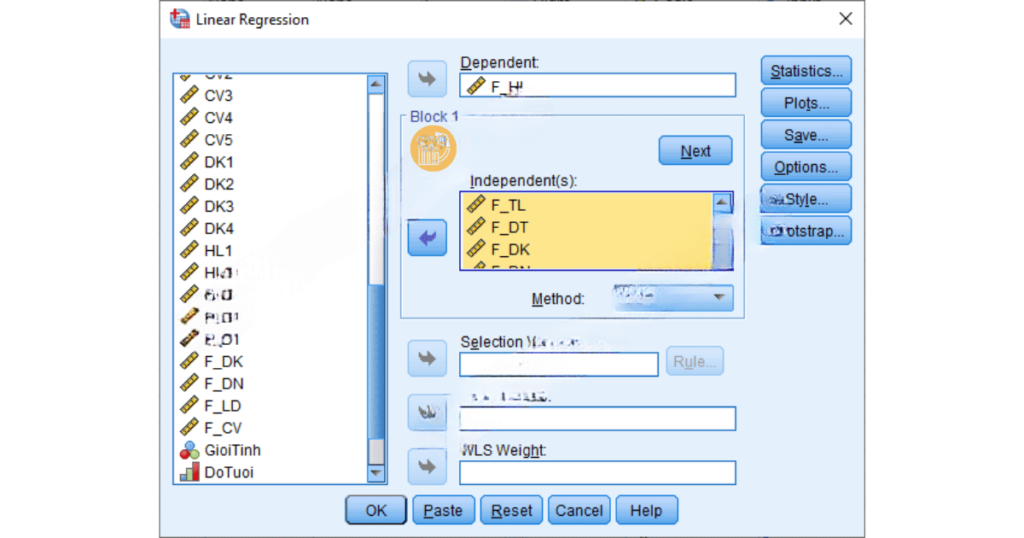
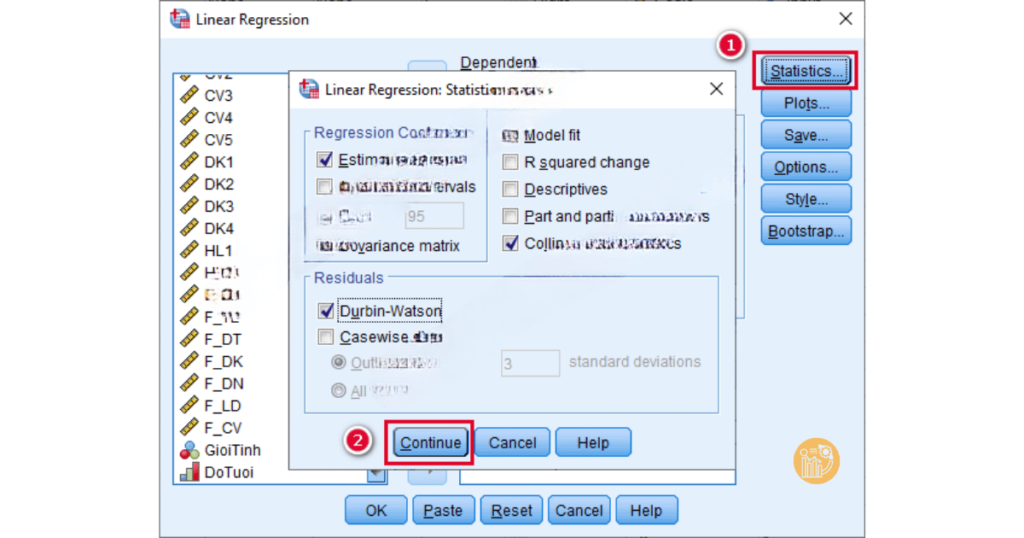
B2: Tùy chỉnh các thống kê và kiểm tra: Trong cửa sổ Linear Regression, bạn có thể chọn thêm các tùy chọn thống kê để xem các thông số như R², kiểm định t, và phân tích ANOVA. Chọn Plots để vẽ các biểu đồ, giúp kiểm tra giả thuyết về phân phối phần dư và quan hệ tuyến tính.
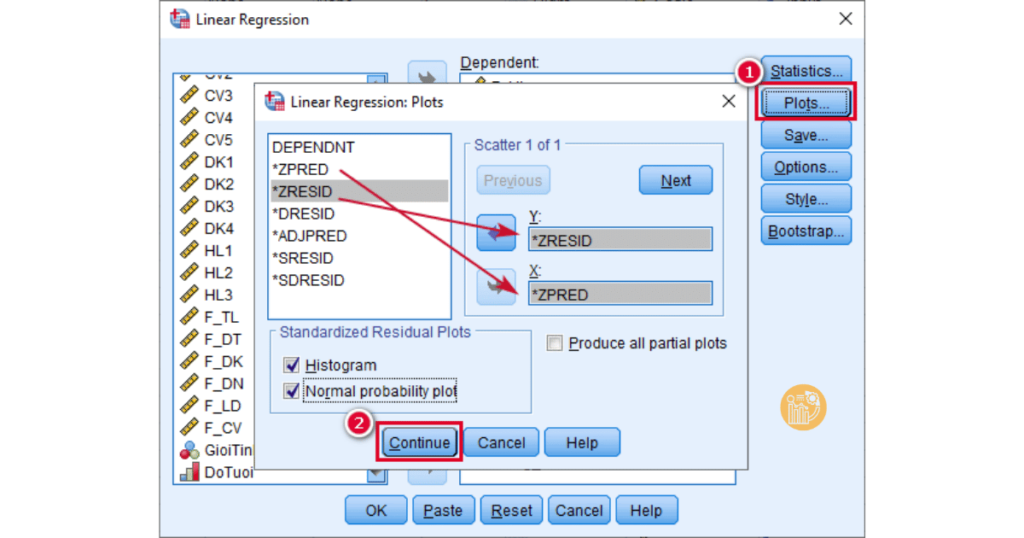
B3: Phương pháp nhập biến: Trong mục Method, bạn có thể chọn phương pháp đưa các biến vào mô hình. Thường dùng phương pháp Enter nếu bạn muốn đưa tất cả các biến độc lập vào một lúc. Nếu cần, bạn có thể sử dụng phương pháp Stepwise để SPSS tự động chọn các biến quan trọng nhất.
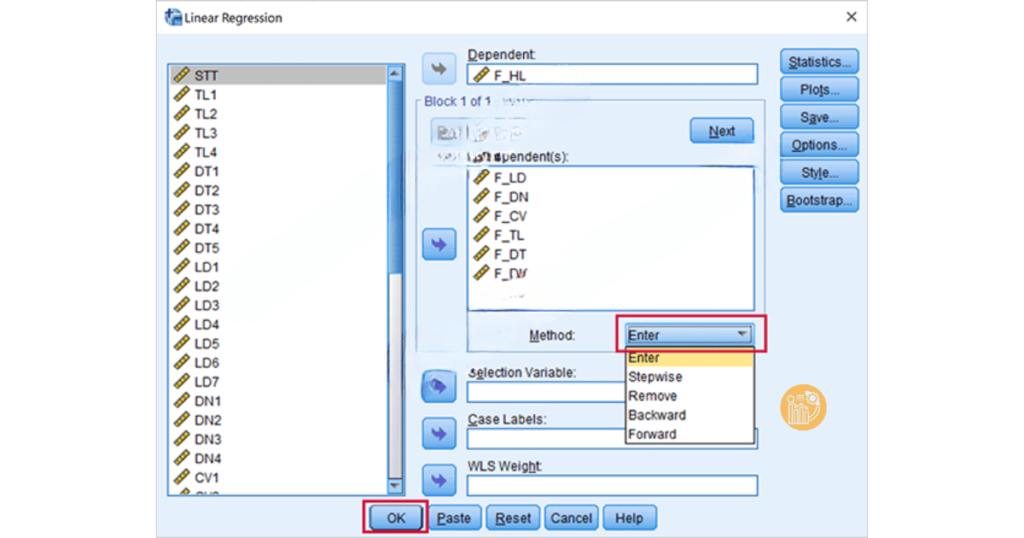
B4: Chạy phân tích và xem kết quả: Sau khi chọn xong các tùy chọn, nhấn OK để SPSS chạy phân tích và xuất ra các bảng kết quả.
Đọc kết quả phân tích hồi quy tuyến tính bội trong SPSS
Bảng ANOVA
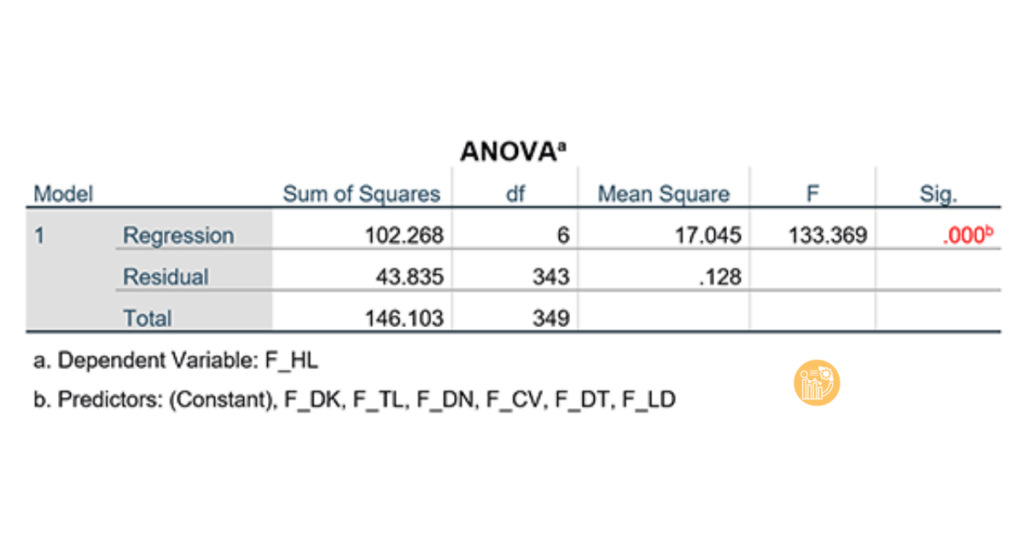
Bảng ANOVA kiểm tra độ phù hợp của mô hình hồi quy. Kiểm định F sẽ được sử dụng để kiểm tra giả thuyết rằng mô hình hồi quy không giải thích được sự biến thiên của biến phụ thuộc.
- Giá trị Sig < 0.05: Mô hình hồi quy phù hợp và có ý nghĩa thống kê.
- Giá trị Sig > 0.05: Mô hình hồi quy không có ý nghĩa thống kê.
Bảng Model Summary

Bảng này cung cấp thông tin về mức độ phù hợp của mô hình. R² là chỉ số quan trọng để đo lường mức độ biến thiên của biến phụ thuộc được giải thích bởi các biến độc lập. Adjusted R² phản ánh mức độ phù hợp của mô hình, có điều chỉnh cho số lượng biến độc lập.
- R² gần 1: Mô hình có mức độ phù hợp cao.
- Adjusted R²: Phản ánh độ chính xác của mô hình khi có nhiều biến độc lập.
Bảng Coefficients
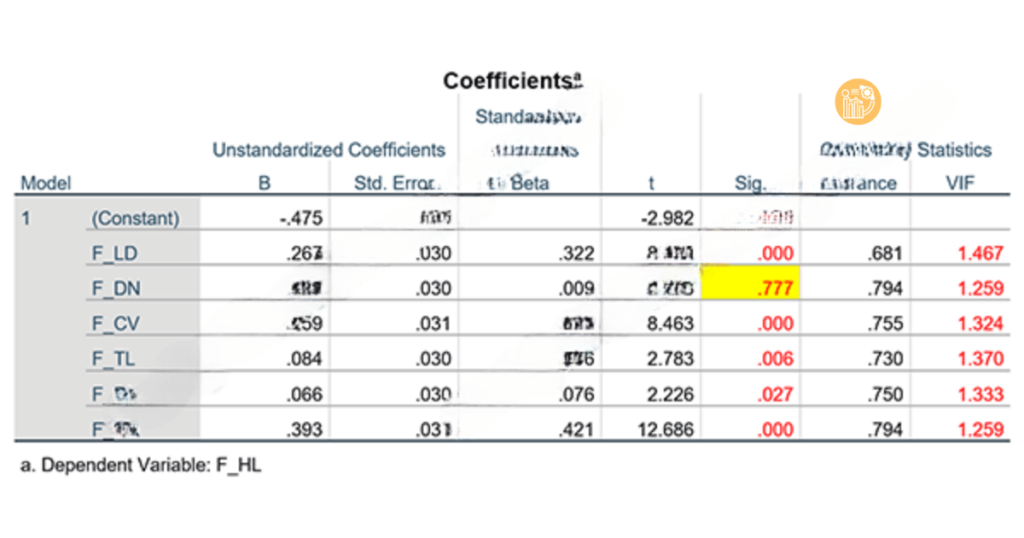
Bảng này là nơi kiểm tra ý nghĩa của các hệ số hồi quy. Bạn cần chú ý đến giá trị SIG của từng biến độc lập:
- SIG < 0.05: Hệ số hồi quy của biến có ý nghĩa thống kê và tác động lên biến phụ thuộc.
- SIG > 0.05: Hệ số hồi quy của biến không có ý nghĩa thống kê và không tác động lên biến phụ thuộc.
Kiểm định và kiểm tra giả thuyết trong hồi quy tuyến tính bội
Khi thực hiện phân tích hồi quy tuyến tính bội, chúng ta cần kiểm định các giả thuyết về mối quan hệ giữa biến phụ thuộc và các biến độc lập. Các kiểm định chính bao gồm:
- Kiểm định F: Đánh giá độ phù hợp của mô hình hồi quy.
- Kiểm định t (t-test): Kiểm tra ý nghĩa của mỗi biến độc lập trong mô hình hồi quy.
- VIF: Kiểm tra vấn đề đa cộng tuyến trong mô hình.
Ví dụ hồi quy tuyến tính bội
Giả sử bạn muốn nghiên cứu sự ảnh hưởng của các yếu tố như tiền lương, đào tạo và thăng tiến, lãnh đạo, và điều kiện làm việc đến sự hài lòng của nhân viên. Mô hình hồi quy tuyến tính bội sẽ giúp bạn xác định mức độ ảnh hưởng của từng yếu tố này.
Phương trình hồi quy có thể có dạng:
Y = 0.322 * F_LD + 0.288 * F_CV + 0.096 * F_TL + 0.076 * F_DT + 0.421 * F_DK + ε
Trong đó:
- Y là sự hài lòng của nhân viên, các biến F_LD, F_CV, F_TL, F_DT, và F_DK là các yếu tố độc lập như lãnh đạo, đồng nghiệp, thăng tiến, đào tạo và điều kiện làm việc.
Kết luận
Phân tích hồi quy tuyến tính bội trong SPSS là một công cụ mạnh mẽ giúp phân tích và dự báo mối quan hệ giữa một biến phụ thuộc và nhiều biến độc lập. Bằng cách hiểu cách đọc các bảng kết quả và kiểm định các giả thuyết, bạn có thể đánh giá chính xác mức độ tác động của các yếu tố đến biến phụ thuộc.
Nếu bạn gặp khó khăn trong việc phân tích dữ liệu hoặc muốn tham khảo thêm các bài viết và hướng dẫn chi tiết về hồi quy tuyến tính bội, hãy truy cập xulysolieu.info hoặc Xử lý số liệu để tìm hiểu thêm và nhận sự trợ giúp từ chuyên gia.
Phương pháp nghiên cứu là gì? Phân loại và quy trình thực hiện chuẩn nhất
Phương pháp nghiên cứu là gì? Đây là câu hỏi quan trọng mà bất kỳ ai trong ngành học thuật hoặc nghiên cứu cũng cần nắm rõ. Phương pháp nghiên cứu khoa học là một quá trình có hệ thống và khách quan, giúp các nhà khoa học điều tra, hiểu và giải thích các hiện tượng trong thế giới xung quanh. Dưới đây, chúng ta sẽ tìm hiểu chi tiết về phương pháp nghiên cứu, phân loại các phương pháp nghiên cứu khoa học, quy trình thực hiện nghiên cứu khoa học và cách chọn phương pháp phù hợp cho từng trường hợp.
Phương pháp nghiên cứu là gì?
Phương pháp nghiên cứu là một cách tiếp cận khoa học, giúp các nhà nghiên cứu thu thập, phân tích và đánh giá dữ liệu để trả lời các câu hỏi nghiên cứu. Quy trình này thường xuyên được sử dụng trong các lĩnh vực khoa học tự nhiên, xã hội, y tế và nhiều ngành khác. Mục tiêu của phương pháp nghiên cứu là tìm ra các giải pháp hoặc lý giải cho những vấn đề thực tế thông qua việc thu thập và phân tích dữ liệu một cách khách quan.
Các loại phương pháp nghiên cứu

Có nhiều loại phương pháp nghiên cứu khác nhau, mỗi loại có ứng dụng phù hợp tùy theo mục đích nghiên cứu. Các phương pháp nghiên cứu khoa học phổ biến bao gồm:
- Phương pháp định tính: Dùng để khám phá các khía cạnh phức tạp của một vấn đề, thường sử dụng các phương pháp như phỏng vấn, quan sát, và phân tích nội dung để thu thập dữ liệu.
- Phương pháp định lượng: Thường sử dụng các công cụ thống kê để thu thập và phân tích dữ liệu số, giúp đưa ra kết luận chính xác, có thể đo lường và kiểm chứng.
- Phương pháp hỗn hợp: Kết hợp cả phương pháp định tính và định lượng để cung cấp một cái nhìn toàn diện về vấn đề nghiên cứu.
Quy trình nghiên cứu khoa học
Quy trình nghiên cứu khoa học là một chuỗi các bước có cấu trúc, giúp các nhà nghiên cứu tiến hành một nghiên cứu một cách có hệ thống và chính xác. Quy trình này bao gồm:
- Quan sát và xây dựng lý thuyết: Đây là bước đầu tiên trong nghiên cứu khoa học. Nhà nghiên cứu quan sát một hiện tượng và xây dựng lý thuyết để giải thích hiện tượng đó.
- Đặt câu hỏi nghiên cứu: Sau khi xây dựng lý thuyết, các nhà nghiên cứu đặt câu hỏi rõ ràng, cụ thể để xác định những vấn đề cần nghiên cứu.
- Hình thành giả thuyết: Dựa trên lý thuyết và câu hỏi nghiên cứu, các nhà khoa học đưa ra giả thuyết – một lời dự đoán về kết quả nghiên cứu.
- Tiến hành thu thập dữ liệu: Các nhà nghiên cứu thực hiện thí nghiệm hoặc thu thập dữ liệu thông qua các phương pháp như khảo sát, phỏng vấn, quan sát trực tiếp.
- Phân tích dữ liệu: Sau khi thu thập dữ liệu, các nhà nghiên cứu sẽ phân tích chúng để xác định các mẫu và mối quan hệ, giúp kiểm chứng giả thuyết.
- Chia sẻ kết quả: Kết quả nghiên cứu sẽ được công bố để cộng đồng khoa học có thể kiểm tra và phát triển thêm.
- Lặp lại: Nghiên cứu khoa học là quá trình liên tục. Các nhà nghiên cứu sẽ cải tiến và điều chỉnh lý thuyết hoặc phương pháp nghiên cứu của mình dựa trên kết quả thu được từ các nghiên cứu trước đó.
Chọn phương pháp nghiên cứu phù hợp
Lựa chọn phương pháp nghiên cứu phù hợp là một yếu tố quan trọng trong quá trình nghiên cứu. Để chọn phương pháp nghiên cứu đúng đắn, bạn cần cân nhắc các yếu tố như:
- Mục tiêu nghiên cứu: Bạn đang tìm kiếm kết luận chính xác và định lượng hay chỉ muốn khám phá các khía cạnh của vấn đề một cách chi tiết hơn?
- Loại dữ liệu: Dữ liệu của bạn là định tính hay định lượng? Bạn sẽ cần sử dụng phương pháp nghiên cứu thích hợp để thu thập và phân tích chúng.
- Khả năng áp dụng: Phương pháp nghiên cứu nào có thể áp dụng dễ dàng và hiệu quả trong môi trường nghiên cứu của bạn?
Ví dụ phương pháp nghiên cứu trong các lĩnh vực khác nhau
- Sinh học: Nghiên cứu tác động của một loại thuốc mới đối với bệnh tật, qua việc thực hiện các thí nghiệm có kiểm soát.
- Tâm lý học: Kiểm tra các giả thuyết về hành vi con người thông qua các thí nghiệm hoặc khảo sát.
- Vật lý: Kiểm tra các lý thuyết về lực và chuyển động của các hạt bằng các phép đo và thí nghiệm chính xác.
- Khoa học xã hội: Nghiên cứu hành vi con người qua khảo sát và phỏng vấn trong các cộng đồng.
Kết luận
Phương pháp nghiên cứu khoa học là công cụ quan trọng giúp chúng ta hiểu và giải thích các hiện tượng trong thế giới xung quanh. Để thực hiện nghiên cứu khoa học hiệu quả, bạn cần phải hiểu rõ các phương pháp nghiên cứu, quy trình nghiên cứu khoa học, cũng như cách chọn phương pháp phù hợp với mục tiêu và dữ liệu nghiên cứu. Qua đó, các nhà nghiên cứu có thể đóng góp vào việc phát triển tri thức và giải quyết các vấn đề thực tiễn trong cuộc sống.
Nếu bạn đang tìm kiếm thêm tài liệu về phương pháp nghiên cứu hoặc các bước cụ thể trong quy trình nghiên cứu, hãy truy cập xulysolieu.info để tìm hiểu thêm những bài viết chất lượng về nghiên cứu học thuật.
Mẫu bảng câu hỏi khảo sát sinh viên theo quy định mới nhất – Đầy đủ & Dễ chỉnh sửa
Khảo sát sinh viên là một công cụ quan trọng giúp các cơ sở giáo dục thu thập phản hồi từ sinh viên, đánh giá các khía cạnh khác nhau của chất lượng đào tạo và môi trường học tập. Để hỗ trợ việc thu thập dữ liệu chính xác, mẫu bảng câu hỏi khảo sát sinh viên phải được thiết kế rõ ràng và dễ hiểu. Bài viết này cung cấp mẫu phiếu khảo sát sinh viên theo quy định mới nhất, giúp bạn dễ dàng chỉnh sửa và sử dụng cho các cuộc khảo sát sinh viên tại các cơ sở giáo dục.
Mẫu bảng câu hỏi khảo sát sinh viên là gì?
Mẫu bảng câu hỏi khảo sát sinh viên là một công cụ giúp thu thập ý kiến, phản hồi từ sinh viên về các vấn đề liên quan đến học tập, giảng dạy, cơ sở vật chất và các dịch vụ của nhà trường. Việc thực hiện khảo sát giúp nhà trường, giảng viên và các bên liên quan hiểu rõ hơn về nhu cầu, kỳ vọng của sinh viên, từ đó điều chỉnh các chương trình đào tạo sao cho phù hợp hơn.
Bảng câu hỏi khảo sát sinh viên có thể bao gồm các câu hỏi về chất lượng giảng dạy, mức độ hài lòng về cơ sở vật chất, môi trường học tập, và các yếu tố khác liên quan đến quá trình học tập và sinh hoạt trong trường.
Các loại mẫu phiếu khảo sát sinh viên phổ biến

Mẫu phiếu khảo sát sinh viên có thể được chia thành nhiều loại khác nhau tùy vào mục đích sử dụng và vấn đề cần khảo sát. Một số mẫu khảo sát sinh viên phổ biến bao gồm:
- Mẫu khảo sát mức độ hài lòng sinh viên: Đánh giá mức độ hài lòng của sinh viên về các yếu tố như cơ sở vật chất, giảng viên, chương trình học, các dịch vụ hỗ trợ học tập.
- Phiếu khảo sát chất lượng giảng dạy: Thu thập ý kiến sinh viên về chất lượng giảng dạy, phương pháp giảng dạy của giảng viên và hiệu quả của các phương pháp học tập được áp dụng.
- Bảng câu hỏi khảo sát học tập: Đánh giá các phương pháp học tập, hiệu quả học tập của sinh viên, giúp nhà trường cải tiến chương trình đào tạo.
- Mẫu khảo sát ý kiến sinh viên: Mẫu này được sử dụng để thu thập các ý kiến đóng góp của sinh viên về các vấn đề liên quan đến học tập và sinh hoạt trong trường.
- Mẫu khảo sát trực tuyến: Mẫu khảo sát này được thiết kế dưới dạng điện tử, cho phép sinh viên tham gia khảo sát qua các thiết bị kết nối internet như điện thoại, máy tính.
Đặc điểm của mẫu phiếu khảo sát sinh viên
Mẫu phiếu khảo sát sinh viên cần có những đặc điểm sau để thu thập thông tin chính xác và hiệu quả:
- Rõ ràng và dễ hiểu: Các câu hỏi phải được diễn đạt rõ ràng, dễ hiểu để sinh viên có thể trả lời một cách chính xác.
- Câu hỏi khách quan: Đảm bảo các câu hỏi không mang tính định hướng, giúp thu thập các phản hồi trung thực từ sinh viên.
- Đa dạng hình thức câu hỏi: Sử dụng các câu hỏi trắc nghiệm, câu hỏi mở và câu hỏi đánh giá để thu thập thông tin đầy đủ.
- Độ dài hợp lý: Phiếu khảo sát không quá dài để sinh viên không cảm thấy mệt mỏi khi tham gia khảo sát.
Mẫu phiếu khảo sát sinh viên (Biểu mẫu khảo sát sinh viên word)
Dưới đây là mẫu phiếu khảo sát sinh viên giúp bạn dễ dàng hình dung và sử dụng cho các cuộc khảo sát tại trường học:
Trường Đại học Hà Nội
Phiếu khảo sát sinh viên
Đây là mẫu phiếu khảo sát để thu thập thông tin từ sinh viên về chất lượng đào tạo, môi trường học tập, và các dịch vụ của nhà trường. Sau khi điền đầy đủ thông tin, vui lòng gửi lại phiếu khảo sát cho đơn vị tổ chức hoặc gửi về địa chỉ: Km 9, Đường Nguyễn Trãi, Phường Văn Quán, Hà Đông, Hà Nội.
I. Thông tin cá nhân
1. Họ và tên: [Điền thông tin] 2. Ngành học: [Điền thông tin] 3. Địa chỉ thường trú: [Điền thông tin] 4. Điện thoại: [Điền thông tin] 5. Email: [Điền thông tin]
II. Thông tin về SVTN đã có việc làm
1. Tên và địa chỉ của cơ quan đang công tác: [Điền thông tin] 2. Mức độ phù hợp của ngành học với công việc: [Điền lựa chọn] ...
III. Đóng góp cho nhà trường
1. Theo anh/chị, môn học nào cần được bổ sung/giảm thời lượng: [Điền thông tin] 2. Những góp ý khác để nâng cao chất lượng đào tạo: [Điền thông tin]
Mẫu phiếu khảo sát sinh viên này có thể được tải về dưới dạng file Word hoặc Google Forms để dễ dàng điền thông tin và chỉnh sửa theo yêu cầu cụ thể của từng trường.
Khảo sát sinh viên giúp cải thiện chất lượng giáo dục
Khảo sát sinh viên là một trong những công cụ quan trọng giúp các trường đại học, cao đẳng thu thập ý kiến, phản hồi từ sinh viên để cải thiện chất lượng giảng dạy và môi trường học tập. Bằng cách sử dụng mẫu phiếu khảo sát sinh viên, nhà trường có thể thu thập được thông tin đáng tin cậy và đưa ra các quyết định cải tiến phù hợp.
Để thiết kế và thực hiện khảo sát hiệu quả, hãy sử dụng các công cụ khảo sát trực tuyến hoặc biểu mẫu khảo sát sinh viên Word dễ dàng chỉnh sửa và phân phối rộng rãi.
Kết luận
Việc sử dụng mẫu phiếu khảo sát sinh viên giúp các cơ sở giáo dục thu thập thông tin phản hồi quan trọng từ sinh viên, từ đó cải thiện chất lượng đào tạo và dịch vụ trong trường. Để tìm hiểu thêm về các mẫu phiếu khảo sát sinh viên và các kỹ thuật phân tích dữ liệu, bạn có thể tham khảo xulysolieu.info, nơi cung cấp tài liệu hữu ích cho việc nâng cao chất lượng giáo dục và nghiên cứu.
Ký hiệu Độ lệch chuẩn là gì? Khái niệm, Công thức & Cách tính chi tiết
Trong phân tích dữ liệu và thống kê, độ lệch chuẩn là một khái niệm quan trọng giúp chúng ta hiểu được mức độ phân tán của một tập dữ liệu. Tuy nhiên, một số người mới tìm hiểu về thống kê có thể chưa nắm rõ về ký hiệu độ lệch chuẩn cũng như công thức tính độ lệch chuẩn. Bài viết này sẽ giải thích chi tiết về ký hiệu độ lệch chuẩn, cách tính độ lệch chuẩn và công thức tính trong các phần mềm như Excel và SPSS.
Ký hiệu Độ lệch chuẩn là gì?
Độ lệch chuẩn là một thước đo dùng để đánh giá mức độ phân tán của các giá trị trong một tập dữ liệu so với giá trị trung bình. Trong thống kê, ký hiệu độ lệch chuẩn phụ thuộc vào việc bạn đang tính cho mẫu hay cho tổng thể. Cụ thể:
- σ (sigma): Ký hiệu độ lệch chuẩn của tổng thể (toàn bộ tập dữ liệu).
- s: Ký hiệu độ lệch chuẩn của mẫu (tập con của tổng thể).
Ví dụ, nếu bạn có một tập dữ liệu về chiều cao của toàn bộ dân số, bạn sẽ sử dụng ký hiệu σ để tính độ lệch chuẩn. Tuy nhiên, nếu bạn chỉ lấy một mẫu ngẫu nhiên từ dân số, bạn sẽ sử dụng ký hiệu s.
Công thức tính độ lệch chuẩn
Công thức tính độ lệch chuẩn sẽ khác nhau tùy vào việc bạn tính cho mẫu hay cho tổng thể. Dưới đây là công thức chi tiết:
Công thức tính độ lệch chuẩn của tổng thể:
σ = √(Σ(xi - μ)² / N)
Trong đó:
- σ: Độ lệch chuẩn của tổng thể.
- xi: Giá trị của phần tử thứ i trong tập dữ liệu.
- μ: Giá trị trung bình của tổng thể.
- N: Số lượng phần tử trong tổng thể.
Công thức tính độ lệch chuẩn của mẫu:
s = √(Σ(xi - x̄)² / (n - 1))
Trong đó:
- s: Độ lệch chuẩn của mẫu.
- xi: Giá trị của phần tử thứ i trong mẫu.
- x̄: Giá trị trung bình của mẫu.
- n: Số lượng phần tử trong mẫu.
Vậy công thức tính độ lệch chuẩn tổng thể và mẫu khác nhau ở điểm là mẫu sử dụng (n – 1) thay vì N để tính toán, điều này giúp sửa chữa sự thiên lệch trong ước lượng độ lệch chuẩn từ mẫu.
Ý nghĩa của độ lệch chuẩn
Độ lệch chuẩn phản ánh mức độ phân tán hoặc sự biến động của các giá trị trong một tập dữ liệu so với giá trị trung bình. Cụ thể:
- Khi độ lệch chuẩn nhỏ, các giá trị trong tập dữ liệu sẽ gần nhau và gần với giá trị trung bình.
- Khi độ lệch chuẩn lớn, các giá trị trong tập dữ liệu sẽ phân tán rộng hơn, xa hơn so với giá trị trung bình.
Độ lệch chuẩn là một chỉ số quan trọng trong nhiều ngành, từ tài chính đến nghiên cứu khoa học xã hội, vì nó giúp người nghiên cứu hiểu được mức độ biến động và sự không ổn định của dữ liệu.
Độ lệch chuẩn trong SPSS
Trong phần mềm phân tích dữ liệu như SPSS, độ lệch chuẩn là một trong những chỉ số cơ bản trong thống kê mô tả. Khi sử dụng SPSS để phân tích dữ liệu, độ lệch chuẩn cho phép bạn đánh giá sự biến động của các giá trị trong một tập dữ liệu. Nếu độ lệch chuẩn thấp, điều đó có nghĩa là các giá trị trong dữ liệu gần nhau và ít thay đổi, ngược lại nếu độ lệch chuẩn cao, các giá trị sẽ phân tán mạnh.
Trong SPSS, bạn có thể tính toán độ lệch chuẩn thông qua menu Analyze > Descriptive Statistics > Descriptives. Kết quả sẽ hiển thị độ lệch chuẩn cùng với các thống kê mô tả khác.
Cách tính độ lệch chuẩn trong Excel
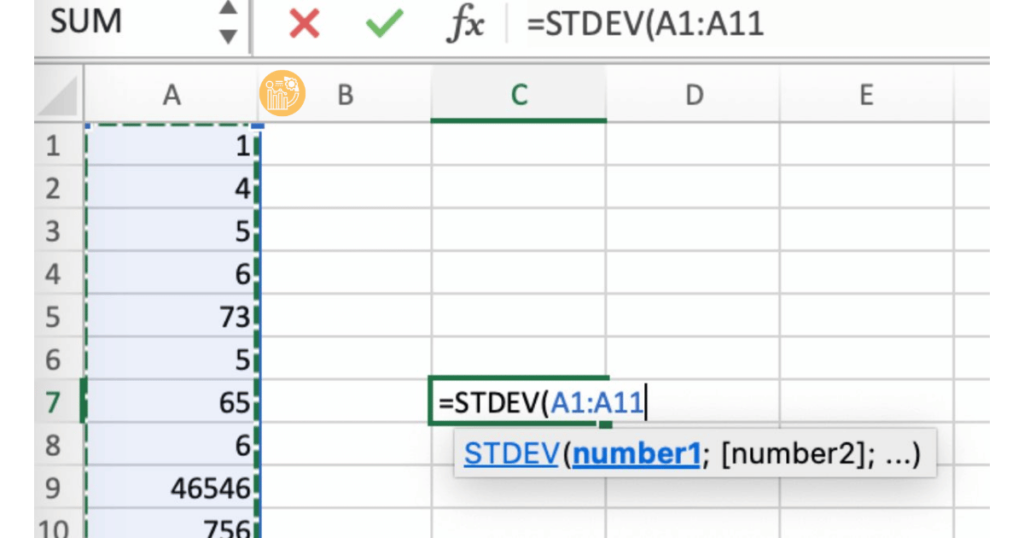
Trong Excel, bạn có thể sử dụng hàm STDEV để tính độ lệch chuẩn của một tập dữ liệu. Cách sử dụng hàm này rất đơn giản:
=STDEV(number1, [number2], ...)
Trong đó:
- number1: Giá trị đầu tiên trong tập dữ liệu.
- number2: Các giá trị bổ sung (tùy chọn).
Ví dụ, để tính độ lệch chuẩn cho một danh sách các giá trị trong ô A1 đến A10, bạn có thể sử dụng công thức sau:
=STDEV(A1:A10)
Mức độ lệch chuẩn nào được coi là chấp nhận được?
Độ lệch chuẩn nhỏ thể hiện rằng dữ liệu có sự tập trung gần với giá trị trung bình, điều này được coi là tốt trong các ngành yêu cầu độ chính xác cao như tài chính, sản xuất. Trong khi đó, độ lệch chuẩn lớn có thể phù hợp với các lĩnh vực có tính đa dạng cao như nghiên cứu hành vi xã hội.
Thông thường, độ lệch chuẩn được coi là ổn định khi:
- Độ lệch chuẩn nhỏ hơn 10% của giá trị trung bình: Dữ liệu ổn định.
- Độ lệch chuẩn lớn hơn 50% của giá trị trung bình: Dữ liệu phân tán quá mức và cần xem xét lại.
Ví dụ về độ lệch chuẩn
Giả sử bạn có một lớp học với các điểm số của học sinh như sau: 2, 2, 4, 4, 4, 5, 5, 7, 9. Để tính độ lệch chuẩn:
- Tính giá trị trung bình: (2 + 2 + 4 + 4 + 4 + 5 + 5 + 7 + 9) / 9 = 4.67.
- Tính phương sai: Bình phương các độ lệch và tính tổng: (2-4.67)² + (2-4.67)² + … = 42.
- Phương sai = 42 / 9 = 5.25.
- Độ lệch chuẩn = √5.25 ≈ 2.29.
Vậy độ lệch chuẩn của điểm số trong lớp học là 2.29.
Kết luận
Hy vọng rằng qua bài viết này, bạn đã hiểu rõ hơn về ký hiệu độ lệch chuẩn, công thức tính và cách sử dụng độ lệch chuẩn trong các phần mềm như Excel và SPSS. Để tìm hiểu thêm các kỹ thuật phân tích dữ liệu khác, hãy truy cập xulysolieu.info, nơi cung cấp nhiều tài liệu hữu ích giúp bạn nâng cao kiến thức trong lĩnh vực thống kê và phân tích dữ liệu.
Kiểm định F trong hồi quy tuyến tính: Ý nghĩa, Công thức & Cách đọc kết quả
Kiểm định F là một công cụ thống kê quan trọng được sử dụng rộng rãi trong các nghiên cứu phân tích dữ liệu. Đặc biệt, nó có vai trò rất lớn trong việc kiểm tra sự khác biệt giữa các nhóm hoặc đánh giá tính phù hợp của mô hình hồi quy. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về kiểm định F, ứng dụng trong hồi quy, cách thực hiện và cách đọc kết quả trong phần mềm SPSS.
Kiểm Định F Là Gì?
Kiểm định F là một kiểm định thống kê được sử dụng để đánh giá sự khác biệt giữa các nhóm hoặc kiểm tra sự phù hợp của mô hình hồi quy. Đây là một kiểm định phân phối F, được thực hiện nhằm xác định xem có sự khác biệt có ý nghĩa thống kê giữa các nhóm hay không, hoặc liệu mô hình hồi quy có phù hợp với dữ liệu.
Công Thức:
F = MS_between / MS_within
Trong đó:
- MS_between (Mean Square Between): là phương sai giữa các nhóm, đo lường sự biến động giữa các nhóm.
- MS_within (Mean Square Within): là phương sai trong các nhóm, đo lường sự biến động trong mỗi nhóm.
Kết quả của kiểm định sẽ cho biết liệu có sự khác biệt giữa các nhóm nghiên cứu hay không. Nếu giá trị F lớn và p-value nhỏ hơn 0.05, có thể kết luận rằng có sự khác biệt có ý nghĩa thống kê giữa các nhóm.
Kiểm Định F trong Hồi Quy
Trong phân tích hồi quy, kiểm định F thường được sử dụng để kiểm tra tính phù hợp của mô hình hồi quy tổng thể. Mục tiêu của kiểm định F trong hồi quy là xác định liệu mô hình hồi quy có phù hợp với dữ liệu và liệu các biến độc lập có tác động đáng kể đến biến phụ thuộc.
Cách thực hiện trong hồi quy:
- Khi thực hiện hồi quy, kiểm định F sẽ được sử dụng để đánh giá xem mô hình hồi quy có giải thích được biến phụ thuộc hay không.
- Trong SPSS, bạn có thể kiểm tra bảng “ANOVA” trong kết quả để xác định p-value của kiểm định F. Nếu p-value nhỏ hơn 0.05, có thể kết luận rằng mô hình hồi quy có tác động đáng kể đến biến phụ thuộc.
Cách kiểm tra giá trị p của kiểm định F trong hồi quy:
- Nếu p-value < 0.05, bạn có thể bác bỏ giả thuyết rằng mô hình hồi quy không có tác động.
- Nếu p-value > 0.05, bạn không thể bác bỏ giả thuyết rằng mô hình hồi quy không có tác động.
Kiểm Định F trong SPSS
Phần mềm SPSS là một công cụ mạnh mẽ trong phân tích thống kê và rất hữu ích khi thực hiện kiểm định F. Để thực hiện kiểm định F trong SPSS, bạn có thể làm theo các bước sau:
1. Thực hiện kiểm định trong hồi quy:
- Mở SPSS và vào menu Analyze > Regression > Linear.
- Chọn biến phụ thuộc (dependent variable) và các biến độc lập (independent variables).
- Khi thực hiện, SPSS sẽ tự động tính toán giá trị F và đưa vào bảng ANOVA. Bạn có thể kiểm tra giá trị p của kiểm định F trong bảng này.
2. Đọc kết quả kiểm định:
- Sau khi thực hiện kiểm định F trong SPSS, kết quả sẽ xuất hiện dưới dạng bảng “ANOVA” hoặc “Levene’s Test” (tuỳ vào loại kiểm định). Trong bảng ANOVA, bạn sẽ thấy giá trị F và p-value. Nếu p-value nhỏ hơn 0.05, bạn có thể kết luận rằng mô hình hồi quy có ý nghĩa thống kê.
- Nếu p-value lớn hơn 0.05, bạn không thể kết luận rằng mô hình hồi quy có tác động đáng kể đến biến phụ thuộc.
Ý Nghĩa Kiểm Định F
Kiểm định F có ý nghĩa rất quan trọng trong việc phân tích sự khác biệt giữa các nhóm hoặc kiểm tra tính phù hợp của mô hình hồi quy. Dưới đây là một số ý nghĩa chính:
- Trong Phân Tích Phương Sai (ANOVA): Kiểm định F giúp xác định xem có sự khác biệt có ý nghĩa thống kê giữa các nhóm hay không. Ví dụ, bạn có thể dùng kiểm định F để so sánh mức độ hài lòng công việc giữa ba nhóm nhân viên khác nhau (nam, nữ và khác).
- Trong Hồi Quy: Kiểm định F giúp kiểm tra xem mô hình hồi quy có đủ khả năng giải thích sự thay đổi của biến phụ thuộc. Ví dụ, bạn có thể dùng kiểm định để kiểm tra xem các biến như độ tuổi, thu nhập có tác động đến mức độ hài lòng công việc hay không.
Cách Đọc Kiểm Định F trong SPSS
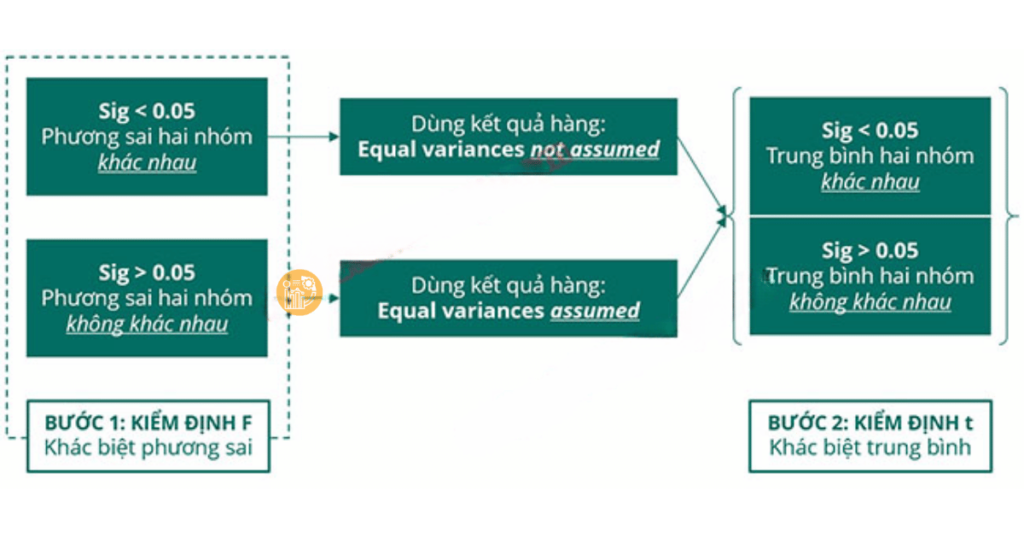
Kết quả trong SPSS có thể xuất hiện dưới dạng bảng “Levene’s Test” (kiểm tra phương sai) hoặc bảng “ANOVA” (kiểm tra hồi quy). Dưới đây là cách đọc kết quả:
1. Levene’s Test (Kiểm Định F Phương Sai):
- Sig < 0.05: Bác bỏ giả thuyết rằng phương sai giữa các nhóm là bằng nhau. Điều này có nghĩa là phương sai của các nhóm là khác nhau và bạn nên sử dụng kết quả kiểm định F ở dòng “Equal variances not assumed”.
- Sig > 0.05: Chấp nhận giả thuyết rằng phương sai giữa các nhóm là bằng nhau. Bạn có thể sử dụng kết quả kiểm định F ở dòng “Equal variances assumed”.
2. ANOVA (Kiểm Định F trong Hồi Quy):
- Sig < 0.05: Bác bỏ giả thuyết không có sự ảnh hưởng từ các biến độc lập đến biến phụ thuộc. Điều này có nghĩa là mô hình hồi quy có ý nghĩa thống kê và các biến độc lập có tác động đến biến phụ thuộc.
- Sig > 0.05: Chấp nhận giả thuyết rằng mô hình hồi quy không có tác động đáng kể đến biến phụ thuộc.
Ví Dụ
Để giúp bạn dễ hiểu hơn, dưới đây là một ví dụ về kiểm định F:
Giả sử bạn muốn nghiên cứu sự khác biệt trong mức độ hài lòng công việc giữa ba nhóm nhân viên trong công ty (nam, nữ, và nhóm khác). Bạn sử dụng kiểm định trong SPSS để kiểm tra sự khác biệt phương sai giữa các nhóm này. Nếu p-value của kiểm định F nhỏ hơn 0.05, bạn có thể kết luận rằng có sự khác biệt có ý nghĩa giữa các nhóm.
Ví Dụ trong Hồi Quy: Giả sử bạn thực hiện hồi quy để nghiên cứu tác động của thu nhập và độ tuổi đối với mức độ hài lòng công việc. Kiểm định F sẽ cho phép bạn xác định liệu mô hình hồi quy có giải thích được sự thay đổi trong mức độ hài lòng công việc hay không.
Kết Luận
Kiểm định F là một công cụ cực kỳ quan trọng trong phân tích thống kê, đặc biệt trong việc kiểm tra sự khác biệt giữa các nhóm hoặc đánh giá tính phù hợp của mô hình hồi quy. Việc thực hiện đúng cách sẽ giúp bạn đưa ra những kết luận chính xác, có cơ sở khoa học cho các nghiên cứu phân tích dữ liệu.
Nếu bạn cần thêm thông tin chi tiết về kiểm định à các kỹ thuật phân tích thống kê khác, hãy tham khảo các tài liệu chuyên sâu tại xulysolieu.info để có thêm kiến thức bổ ích trong việc áp dụng trong phân tích dữ liệu.
Độ phù hợp của mô hình hồi quy qua R² và R² hiệu chỉnh
Trong phân tích hồi quy, một công việc quan trọng không chỉ là ước lượng mối quan hệ giữa các biến mà còn là đánh giá mức độ phù hợp của mô hình với dữ liệu thực tế. Để làm được điều này, người phân tích thường sử dụng R bình phương (R²) và R bình phương hiệu chỉnh (Adjusted R²) – hai chỉ số cốt lõi giúp xác định mô hình hồi quy tuyến tính có phản ánh đúng dữ liệu hay không.
1. R² là gì?
R bình phương (R²), hay còn gọi là hệ số xác định, là chỉ số phản ánh tỷ lệ phần trăm biến thiên của biến phụ thuộc (Y) được giải thích bởi các biến độc lập (X) trong mô hình hồi quy tuyến tính.
Về bản chất, R² được tính từ ý tưởng rằng tổng biến thiên của Y có thể chia làm hai phần:
- Biến thiên do hồi quy (Regression Sum of Squares – SSR): phần biến thiên được mô hình giải thích.
- Biến thiên do phần dư (Residual Sum of Squares – SSE): phần biến thiên không được mô hình giải thích.
Công thức tổng quát: R2=1−SSESSTR^2 = 1 – \frac{SSE}{SST}R2=1−SSTSSE
trong đó:
- SSE: Tổng bình phương sai số,
- SST: Tổng bình phương độ lệch của Y so với trung bình.
Khi SSE càng nhỏ, nghĩa là các điểm dữ liệu càng gần đường hồi quy → mô hình càng phù hợp → R² càng cao.
Tuy nhiên, một nhược điểm lớn của R² là nó luôn tăng khi bạn thêm nhiều biến độc lập vào mô hình – kể cả khi những biến này không thật sự có ý nghĩa thống kê. Điều đó khiến R² có xu hướng “thổi phồng” độ phù hợp của mô hình.
2. R² hiệu chỉnh là gì? — Phiên bản trung thực hơn của R²

Để khắc phục nhược điểm trên, người ta sử dụng R bình phương hiệu chỉnh (Adjusted R²).
Chỉ số này điều chỉnh R² dựa trên số lượng biến độc lập và kích thước mẫu, phản ánh mức độ phù hợp thực sự của mô hình hồi quy.
Công thức: Rhiệu chỉnh2=1−(1−R2)(n−1)n−k−1R^2_{hiệu\ chỉnh} = 1 – \frac{(1 – R^2)(n – 1)}{n – k – 1}Rhiệu chỉnh2=1−n−k−1(1−R2)(n−1)
trong đó:
- n: số quan sát,
- k: số biến độc lập.
Khi thêm một biến mới vào mô hình:
- Nếu biến đó thực sự giúp cải thiện mô hình, Adjusted R² sẽ tăng.
- Nếu biến không có ý nghĩa, Adjusted R² sẽ giảm.
Do đó, R² hiệu chỉnh luôn nhỏ hơn hoặc bằng R², và được xem là thước đo đáng tin cậy hơn khi đánh giá mô hình hồi quy đa biến.
3. Ý nghĩa của R² hiệu chỉnh trong thực tế
Giống như R², chỉ số R² hiệu chỉnh dao động từ 0 đến 1:
- Giá trị càng gần 1 → mô hình càng giải thích tốt biến phụ thuộc.
- Giá trị càng gần 0 → mô hình giải thích kém.
Ví dụ:
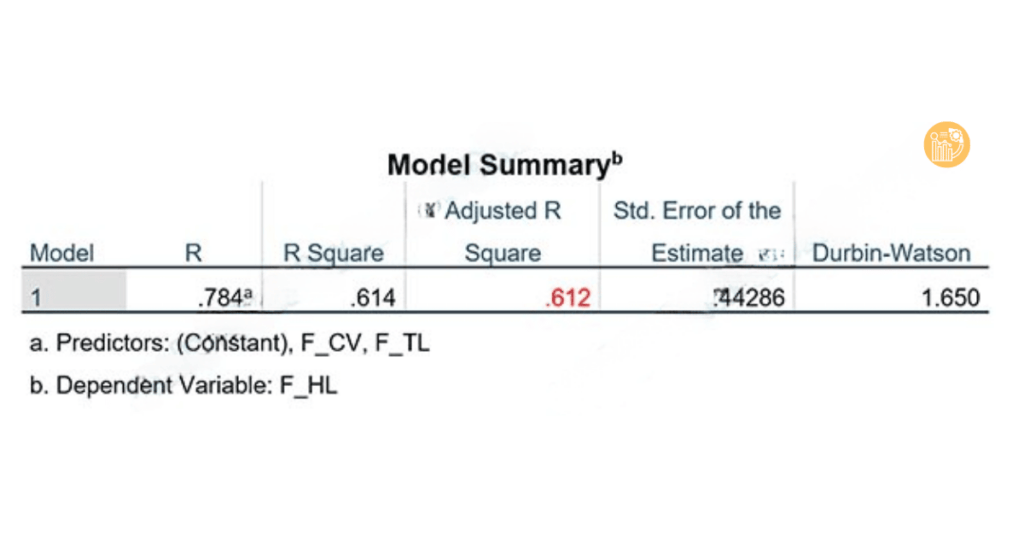
Giả sử trong kết quả hồi quy SPSS, Adjusted R² = 0.725, điều đó có nghĩa:
Các biến độc lập trong mô hình giải thích được 72.5% sự biến thiên của biến phụ thuộc.
Phần còn lại 27.5% là do các yếu tố chưa được đưa vào mô hình và sai số ngẫu nhiên.
4. Khi R² hiệu chỉnh dưới 0.5 — Có phải mô hình kém?
Nhiều người cho rằng R² hiệu chỉnh phải trên 0.5 (50%) thì mô hình mới “đạt yêu cầu”, nhưng thực tế không có tiêu chuẩn cố định nào như vậy.
Mức độ phù hợp của mô hình phụ thuộc vào:
- Tính chất của hiện tượng nghiên cứu,
- Số lượng biến độc lập,
- Độ chính xác của dữ liệu,
- Ngành khoa học cụ thể.
Trong một số lĩnh vực xã hội, hành vi, hoặc marketing, Adjusted R² < 0.5 vẫn hoàn toàn chấp nhận được, miễn là các biến có ý nghĩa thống kê và mô hình phù hợp về mặt lý thuyết.
Nói cách khác, R² hiệu chỉnh chỉ là thước đo tham khảo, không nên dùng để bác bỏ mô hình một cách cứng nhắc.
5. Cách tăng giá trị R² & R² hiệu chỉnh trong SPSS
Nếu kết quả hồi quy của bạn cho thấy R² hiệu chỉnh thấp, có thể cải thiện bằng các cách sau:
5.1. Loại bỏ các giá trị ngoại lai (Outliers) qua đồ thị Scatter Plot

Các điểm dị biệt (outliers) thường làm sai lệch mô hình và kéo giảm giá trị R² hiệu chỉnh.
Trong SPSS, bạn có thể phát hiện chúng bằng cách:
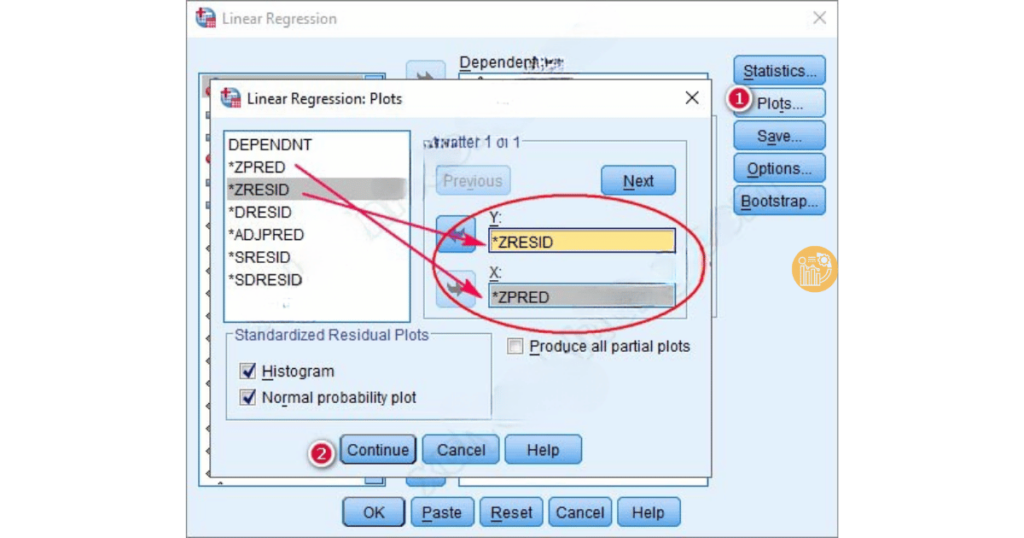
- Vào Plots, kéo ZRESID vào ô Y và ZPRED vào ô X.
- Quan sát đồ thị Scatter Plot:
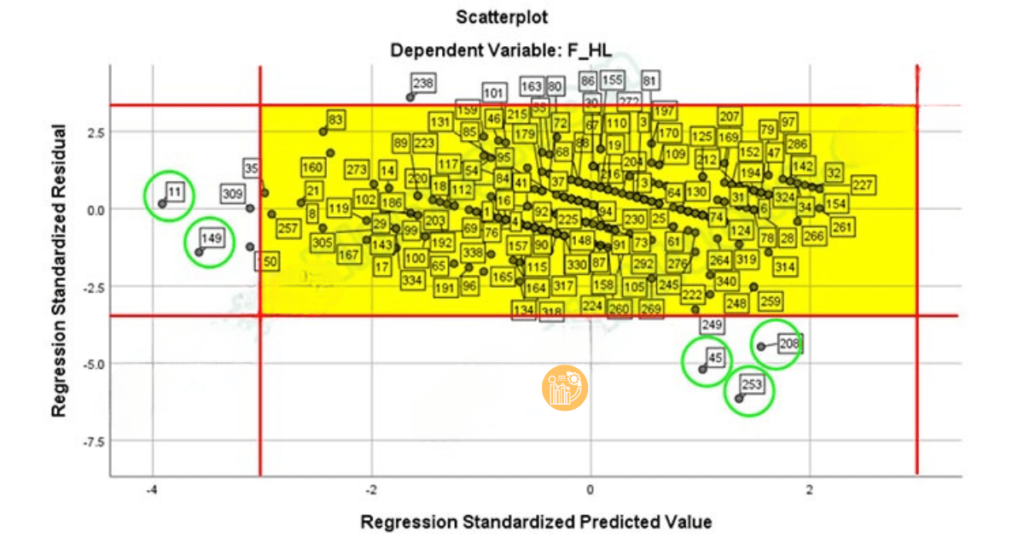
Các điểm nằm ngoài vùng −3,3-3, 3−3,3 theo quy luật Empirical 68–95–99.7 là các giá trị ngoại lai.
Ví dụ: mô hình hồi quy giữa F_TL, F_CV → F_HL ban đầu có Adjusted R² = 0.478.
Sau khi loại bỏ 5 điểm dị biệt (ID: 11, 45, 149, 208, 253), Adjusted R² tăng lên 0.553, chứng tỏ mô hình đã phù hợp hơn đáng kể.

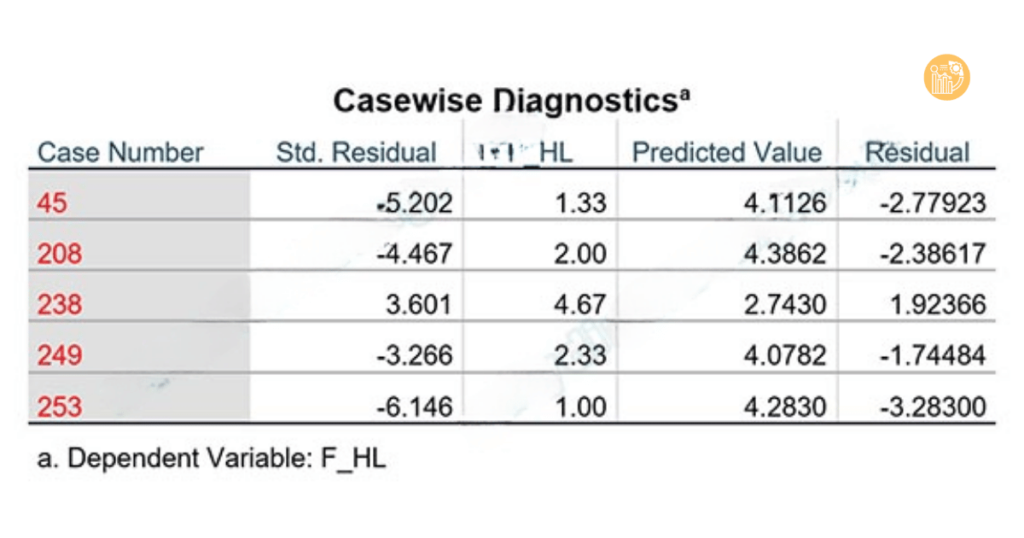
5.2. Sử dụng bảng Casewise Diagnostics trong SPSS
SPSS hỗ trợ phát hiện tự động điểm dị biệt:
- Chọn Statistics → Casewise Diagnostics,
- Nhập giá trị 3 trong ô Outliers outside, để xác định các quan sát nằm ngoài vùng ±3 độ lệch chuẩn.
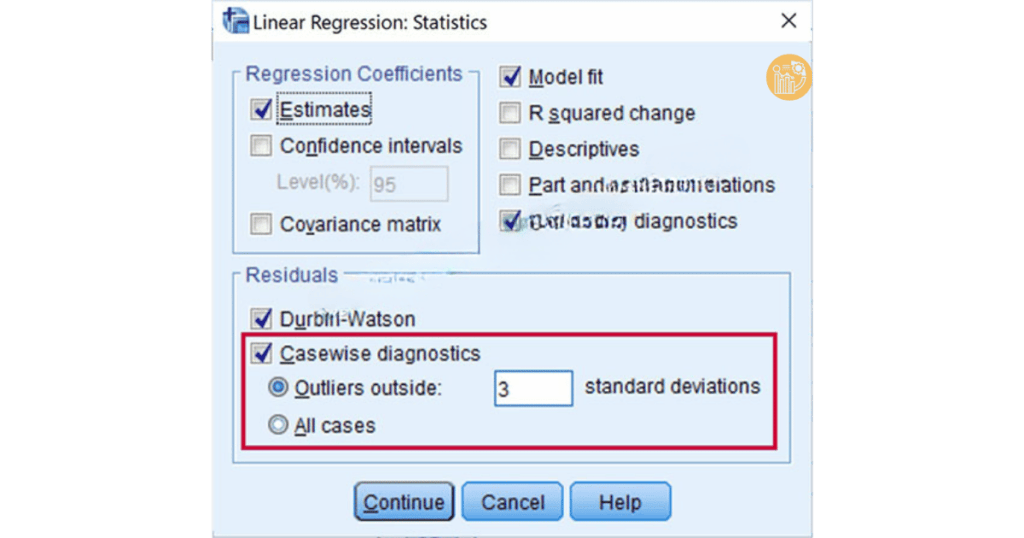
Sau khi loại bỏ các điểm này, Adjusted R² có thể tăng đáng kể.
Ví dụ: loại bỏ các quan sát 45, 208, 238, 249, 253 giúp mô hình tăng Adjusted R² từ 0.478 lên 0.612, thể hiện sự cải thiện rõ rệt về độ phù hợp.
6. Kết luận
R bình phương hiệu chỉnh là chỉ số then chốt giúp đánh giá mức độ phù hợp thực chất của mô hình hồi quy tuyến tính.
Khác với R² thông thường, chỉ số hiệu chỉnh phản ánh độ chính xác sau khi đã loại trừ ảnh hưởng “ảo” của việc thêm biến độc lập.
Một mô hình tốt không nhất thiết phải có Adjusted R² cao vượt trội, mà cần:
- Các biến có ý nghĩa thống kê,
- Phù hợp về lý thuyết,
- Không vi phạm giả định hồi quy,
- Không bị ảnh hưởng bởi các giá trị ngoại lai.
Do đó, khi phân tích hồi quy trong SPSS, hãy ưu tiên xem xét R² hiệu chỉnh thay vì R² thuần túy, và chủ động kiểm tra – loại bỏ outlier để đảm bảo mô hình phản ánh đúng thực tế.
PCA là gì? Kiến thức cần có về Principal Component Analysis
Trong thời đại dữ liệu bùng nổ, việc xử lý các tập dữ liệu có hàng trăm hoặc hàng nghìn biến (đặc trưng) là một thách thức lớn đối với các nhà khoa học dữ liệu. Principal Component Analysis – PCA là gì? – hay còn gọi là phân tích thành phần chính – chính là một trong những kỹ thuật giảm chiều dữ liệu phổ biến nhất, giúp đơn giản hóa dữ liệu phức tạp mà vẫn giữ lại phần lớn thông tin quan trọng.
Bài viết này sẽ giúp bạn hiểu PCA là gì, cách PCA hoạt động, ưu – nhược điểm, và những ứng dụng thực tế trong khoa học dữ liệu và học máy (machine learning).
1. PCA là gì?
PCA (Principal Component Analysis) là một phương pháp thống kê dùng để giảm chiều dữ liệu (dimensionality reduction), bằng cách biến đổi tập hợp nhiều biến có tương quan thành một tập hợp biến mới không tương quan gọi là các thành phần chính (principal components).
Mục tiêu của PCA là giảm số lượng đặc trưng của dữ liệu mà vẫn giữ được tối đa thông tin (phương sai) ban đầu. Nói cách khác, PCA giúp bạn nén dữ liệu phức tạp thành dạng cô đọng hơn nhưng vẫn “đủ ý nghĩa” cho việc phân tích hoặc huấn luyện mô hình học máy.
Ví dụ, một bộ dữ liệu có 100 biến đầu vào, PCA có thể giảm xuống còn 10 hoặc 20 biến chính mà vẫn thể hiện được phần lớn thông tin cốt lõi.
2. Tại sao nên dùng PCA?
Khi làm việc với các bộ dữ liệu lớn, việc xử lý quá nhiều biến có thể dẫn đến:
- Mô hình phức tạp, dễ overfitting
- Thời gian huấn luyện lâu
- Khó trực quan hóa dữ liệu
- Hiện tượng đa cộng tuyến (multicollinearity)
PCA giúp khắc phục các vấn đề này thông qua những lợi ích sau:
- ✅ Thu gọn không gian đặc trưng: Giảm số biến, đơn giản hóa mô hình mà vẫn giữ được độ chính xác cao.
- ✅ Loại bỏ thông tin nhiễu: PCA tập trung vào các hướng có phương sai lớn nhất – tức là nơi dữ liệu thay đổi mạnh mẽ và có ý nghĩa nhất.
- ✅ Tăng tốc độ và hiệu suất mô hình: Giảm chiều giúp rút ngắn thời gian huấn luyện và tăng khả năng khái quát.
- ✅ Phát hiện dữ liệu bất thường (outlier detection): PCA có thể chỉ ra những điểm dữ liệu lệch khỏi cấu trúc chính của dữ liệu.
3. PCA hoạt động như thế nào?

Về mặt toán học, PCA hoạt động dựa trên đại số tuyến tính và ma trận hiệp phương sai (covariance matrix). Quá trình có thể được tóm tắt như sau:
- Chuẩn hóa dữ liệu (standardization): Đưa tất cả các biến về cùng thang đo.
- Tính ma trận hiệp phương sai, thể hiện mối tương quan giữa các biến.
- Tính toán các giá trị riêng (eigenvalues) và vectơ riêng (eigenvectors) của ma trận hiệp phương sai.
- Các vectơ riêng xác định hướng biến thiên lớn nhất trong dữ liệu.
- Các giá trị riêng thể hiện độ quan trọng của từng hướng đó.
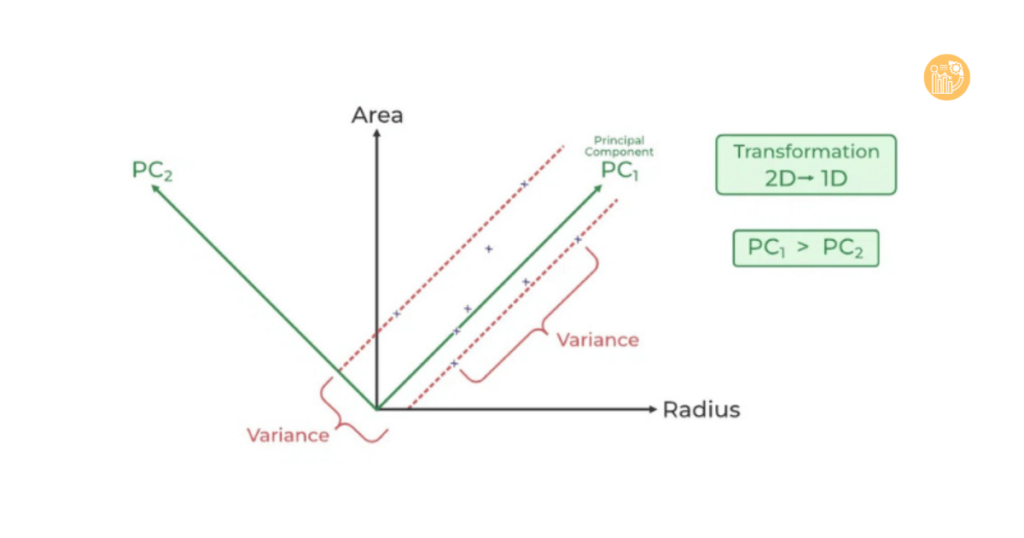
- Sắp xếp các thành phần chính (principal components) theo thứ tự giảm dần của phương sai.
- Chiếu dữ liệu gốc lên các thành phần chính để tạo ra bộ dữ liệu mới có số chiều thấp hơn.
Ví dụ, nếu bạn chọn hai thành phần đầu tiên (PC1 và PC2), bạn có thể biểu diễn dữ liệu 100 chiều ban đầu trên mặt phẳng 2D mà vẫn giữ được phần lớn thông tin.
4. Ưu và nhược điểm của PCA
Ưu điểm
- Giảm đa cộng tuyến: PCA tạo ra các biến mới không tương quan, giúp ổn định mô hình hồi quy.
- Lọc nhiễu dữ liệu: Loại bỏ các thành phần có phương sai thấp – thường là nhiễu.
- Nén dữ liệu hiệu quả: Giảm nhu cầu lưu trữ và tăng tốc xử lý dữ liệu.
- Phát hiện outlier: PCA chỉ ra các điểm lệch khỏi hướng chính của dữ liệu.
- Cải thiện khả năng trực quan hóa: Cho phép biểu diễn dữ liệu nhiều chiều trên mặt phẳng 2D hoặc 3D.
Nhược điểm
- ❌ Khó giải thích ý nghĩa các thành phần mới, vì chúng là tổ hợp tuyến tính của nhiều biến gốc.
- ❌ Nhạy cảm với tỷ lệ dữ liệu – nếu không chuẩn hóa đúng, kết quả có thể sai lệch.
- ❌ Mất một phần thông tin khi giảm chiều quá mạnh.
- ❌ Giả định mối quan hệ tuyến tính, không phù hợp cho dữ liệu phi tuyến tính.
- ❌ Tốn tài nguyên tính toán khi xử lý dữ liệu cực lớn.
5. Ứng dụng thực tế của PCA
PCA được ứng dụng rộng rãi trong khoa học dữ liệu, thị giác máy tính, và cả lĩnh vực y sinh. Dưới đây là một số ví dụ điển hình:
1. Nén hình ảnh (Image Compression)
PCA giúp giảm số chiều của hình ảnh (pixel), từ đó tiết kiệm dung lượng lưu trữ mà vẫn giữ được các đặc trưng quan trọng.
2. Trực quan hóa dữ liệu (Data Visualization)
PCA chiếu dữ liệu nhiều chiều về không gian 2D hoặc 3D, giúp người phân tích dễ dàng phát hiện cụm, xu hướng hoặc điểm bất thường.
3. Lọc nhiễu dữ liệu (Noise Reduction)
PCA loại bỏ các thành phần có phương sai thấp – thường là phần nhiễu, giúp dữ liệu “sạch” và rõ ràng hơn.
4. Ứng dụng trong y học – Dự đoán ung thư vú
Một nghiên cứu tại Đại học Wisconsin đã áp dụng PCA kết hợp Logistic Regression để dự đoán khả năng mắc ung thư vú, cho thấy PCA giúp mô hình hoạt động nhanh và chính xác hơn nhờ loại bỏ biến dư thừa.
5. Tiền xử lý trong Machine Learning
PCA thường được dùng trước khi huấn luyện các mô hình học máy như hồi quy logistic, SVM, KNN, giúp tăng hiệu suất và giảm overfitting.
6. So sánh PCA và K-means Clustering
| Tiêu chí | PCA | K-means Clustering |
|---|---|---|
| Mục tiêu | Giảm chiều dữ liệu | Phân nhóm dữ liệu |
| Loại học máy | Không giám sát (Unsupervised) | Không giám sát |
| Kết quả | Các thành phần chính (biến mới) | Các cụm dữ liệu (clusters) |
| Dạng biến đổi | Tuyến tính (linear transformation) | Phân nhóm dựa trên khoảng cách |
| Ứng dụng chính | Tiền xử lý, trực quan hóa, nén dữ liệu | Phân nhóm khách hàng, ảnh, hành vi |
Cả hai đều là công cụ mạnh trong học máy, nhưng PCA tập trung vào giảm chiều, trong khi K-means tập trung vào phân cụm (clustering).
7. Khi nào nên sử dụng PCA?
Bạn nên cân nhắc áp dụng PCA khi:
- Bộ dữ liệu có rất nhiều biến và mối tương quan cao
- Cần trực quan hóa dữ liệu nhiều chiều
- Muốn giảm nhiễu và cải thiện hiệu suất mô hình
- Muốn chuẩn bị dữ liệu trước khi huấn luyện mô hình học máy
Ngược lại, nếu dữ liệu có mối quan hệ phi tuyến tính, bạn nên xem xét các kỹ thuật khác như t-SNE, UMAP hoặc LDA (Linear Discriminant Analysis).
8. Kết luận
Qua bài viết này, bạn đã hiểu rõ PCA là gì, nguyên lý hoạt động, cùng những ưu điểm, nhược điểm và ứng dụng thực tế của Principal Component Analysis.
Tóm lại, PCA là công cụ không thể thiếu trong xử lý dữ liệu và học máy, giúp giảm chiều, loại bỏ nhiễu, tăng tốc độ mô hình mà vẫn giữ lại phần lớn thông tin quan trọng. Tuy nhiên, cần sử dụng PCA đúng cách – đặc biệt là chuẩn hóa dữ liệu và chọn số thành phần phù hợp – để đảm bảo kết quả chính xác và có ý nghĩa.
P Value Là Gì? Ý Nghĩa, Phương Pháp Sử Dụng Trong Nghiên Cứu
P value là gì là câu hỏi quen thuộc với bất kỳ ai đang học hoặc làm việc trong lĩnh vực thống kê, kinh tế, xã hội học hay nghiên cứu khoa học. Đây là một khái niệm cốt lõi giúp đánh giá mức độ tin cậy của các kiểm định thống kê, đóng vai trò quyết định trong việc bác bỏ hoặc chấp nhận giả thuyết nghiên cứu. Bài viết dưới đây sẽ giúp bạn hiểu rõ khái niệm p-value, cách tính, ý nghĩa và cách sử dụng hiệu quả trong nghiên cứu thực tế.
P Value Là Gì?
P-value (viết tắt của “probability value”) là giá trị xác suất biểu thị mức độ mà dữ liệu thu được ủng hộ hay phản đối giả thuyết không (Null Hypothesis – H₀). Nói cách khác, p-value cho biết xác suất để xảy ra kết quả quan sát (hoặc kết quả còn cực đoan hơn) trong trường hợp giả thuyết H₀ là đúng.
Giả thuyết thống kê thường bao gồm hai phần:
- Giả thuyết không (H₀): Không có sự khác biệt hay tác động đáng kể giữa các nhóm hoặc biến nghiên cứu.
- Giả thuyết thay thế (H₁): Có sự khác biệt hoặc tác động đáng kể giữa các nhóm hoặc biến nghiên cứu.
Khi tiến hành kiểm định, ta so sánh giá trị p-value với mức ý nghĩa (alpha) thường đặt là 0.05 hoặc 0.01 để ra quyết định:
- Nếu p-value ≤ α: Có đủ bằng chứng để bác bỏ giả thuyết H₀. Kết quả được coi là có ý nghĩa thống kê.
- Nếu p-value > α: Không có đủ bằng chứng để bác bỏ H₀. Kết quả được xem là không có ý nghĩa thống kê.
Ví dụ: Khi kiểm định xem “thu nhập của hai nhóm A và B có khác biệt hay không”, nếu p-value = 0.02 và α = 0.05, ta kết luận có sự khác biệt có ý nghĩa thống kê giữa hai nhóm.
Cách Tính Giá Trị P-Value
Giá trị p-value được tính dựa trên phân phối xác suất của thống kê kiểm định (như z, t, F, hoặc chi-square). Trong thực tế, bạn có thể tính p-value bằng nhiều cách khác nhau, phổ biến nhất là sử dụng phần mềm thống kê như SPSS, R, Excel hoặc Python.
Bước 1: Xác định giả thuyết kiểm định
Xác định rõ H₀ và H₁. Ví dụ: H₀ = “Trung bình nhóm 1 bằng nhóm 2”; H₁ = “Trung bình nhóm 1 khác nhóm 2”.
Bước 2: Chọn loại kiểm định phù hợp
Tùy theo mục tiêu nghiên cứu và loại dữ liệu:
- Kiểm định t (T-test): Dùng cho so sánh trung bình giữa hai nhóm.
- Kiểm định ANOVA: Dùng để so sánh trung bình từ ba nhóm trở lên.
- Kiểm định Chi-square: Dùng cho dữ liệu định tính hoặc kiểm tra tính độc lập giữa các biến.
- Hồi quy tuyến tính: Dùng để xác định ảnh hưởng của biến độc lập đến biến phụ thuộc; p-value được tính cho từng hệ số hồi quy.
Bước 3: Tính toán và đọc kết quả
Phần mềm thống kê sẽ tự động trả về giá trị p-value. Dựa trên giá trị này, bạn đưa ra kết luận về việc chấp nhận hay bác bỏ giả thuyết H₀.
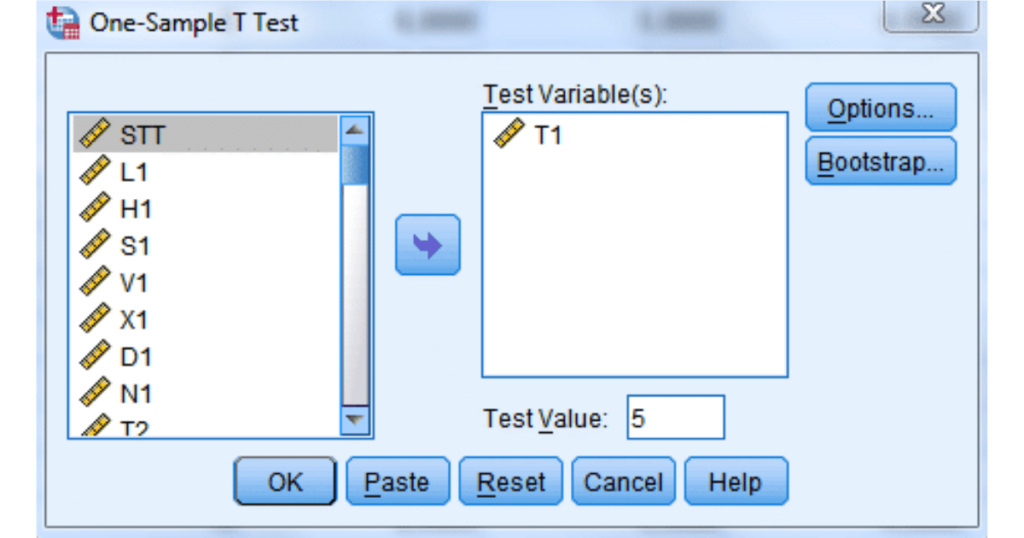
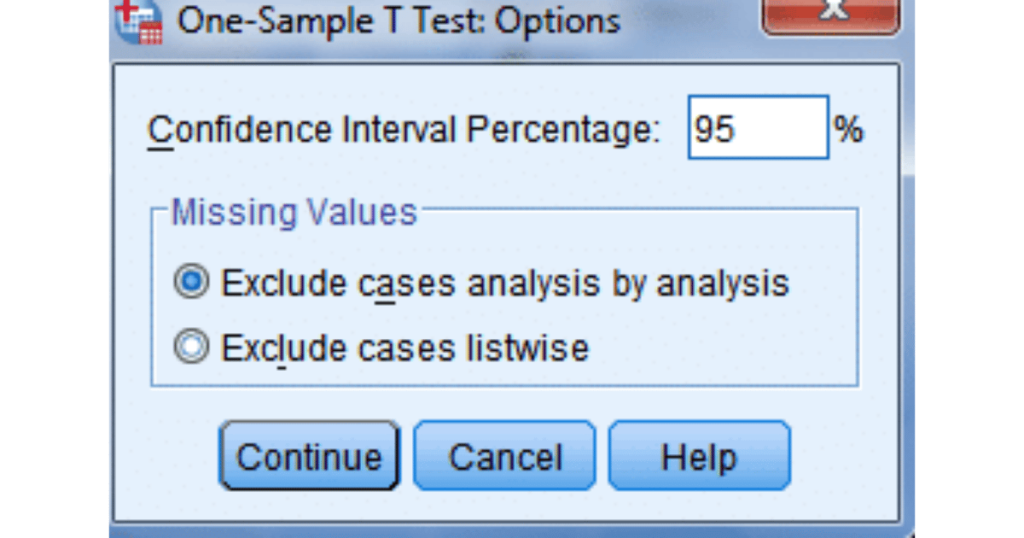

Ý Nghĩa Của Giá Trị P-Value
Trong phân tích thống kê, việc hiểu rõ ý nghĩa của p-value là yếu tố then chốt để diễn giải đúng kết quả nghiên cứu:
- P ≤ 0.01: Kết quả có ý nghĩa thống kê rất mạnh. Có thể bác bỏ H₀ với mức tin cậy cao (99%).
- P ≤ 0.05: Kết quả có ý nghĩa thống kê. Có thể bác bỏ H₀ với độ tin cậy 95%.
- P > 0.05: Không có đủ bằng chứng để bác bỏ H₀. Kết quả không có ý nghĩa thống kê.
Điều quan trọng cần lưu ý: p-value không cho biết xác suất H₀ đúng hay sai, mà chỉ cho biết xác suất quan sát dữ liệu hiện có nếu H₀ là đúng. Do đó, việc diễn giải p-value cần đặt trong bối cảnh nghiên cứu, kích thước mẫu và các giả định thống kê.
Ứng Dụng Của P-Value Trong Nghiên Cứu
Giá trị p-value được ứng dụng rộng rãi trong nhiều lĩnh vực nghiên cứu và thực tiễn, đặc biệt là trong các phân tích thống kê, kiểm định giả thuyết, và mô hình dự đoán:
Kiểm định giả thuyết thống kê
P-value là công cụ cơ bản giúp xác định xem có sự khác biệt hoặc tác động đáng kể giữa các nhóm hay không. Ví dụ: so sánh hiệu quả của hai phương pháp điều trị, hay kiểm tra sự khác biệt giữa hai chiến lược marketing.
Phân tích hồi quy và xác định biến quan trọng
Trong hồi quy tuyến tính hoặc logistic, mỗi hệ số hồi quy đều đi kèm với một p-value. Nếu p-value của biến độc lập < 0.05, biến đó được xem là có ảnh hưởng có ý nghĩa đến biến phụ thuộc.
Phân tích ANOVA
Trong Analysis of Variance, p-value được dùng để kiểm tra xem có sự khác biệt đáng kể giữa trung bình của nhiều nhóm hay không.
Kiểm định Chi-square
P-value giúp xác định tính độc lập giữa hai biến định tính, chẳng hạn như giới tính và lựa chọn sản phẩm.
Nghiên cứu y học và khoa học xã hội
Trong y học, p-value giúp xác định liệu một phương pháp điều trị có hiệu quả thực sự hay không. Trong khoa học xã hội, nó giúp đánh giá mối quan hệ giữa các yếu tố như thu nhập, trình độ học vấn, hành vi tiêu dùng…
Lưu Ý Khi Diễn Giải P-Value
- P-value nhỏ không đồng nghĩa với tác động mạnh; nó chỉ cho biết kết quả có ý nghĩa thống kê.
- Nên xem xét kích thước mẫu (sample size), hiệu quả tác động (effect size) và khoảng tin cậy (confidence interval) song song với p-value để có đánh giá toàn diện.
- Tránh “lạm dụng” p-value – việc quá chú trọng ngưỡng 0.05 có thể dẫn đến sai lệch trong kết luận khoa học.
Kết Luận
Hiểu rõ p value là gì giúp bạn đọc và diễn giải kết quả thống kê một cách chính xác, từ đó đưa ra quyết định khoa học và đáng tin cậy hơn. Dù là trong nghiên cứu học thuật hay phân tích thực tế, p-value vẫn là công cụ nền tảng giúp đánh giá ý nghĩa thống kê của dữ liệu.
Hy vọng bài viết đã giúp bạn nắm vững khái niệm, cách tính và ứng dụng của p-value trong nghiên cứu. Nếu bạn đang làm luận văn hoặc phân tích dữ liệu bằng SPSS, hãy nhớ rằng p-value chỉ là một phần trong bức tranh thống kê toàn diện — cần kết hợp với các chỉ số khác để đưa ra kết luận chính xác và khách quan nhất.
Dữ liệu ngoại lai – outlier là gì? Những cách xử lý dữ liệu này trong phân tích
Outlier là gì? Trong quá trình làm việc với dữ liệu, đôi khi bạn sẽ bắt gặp những giá trị khác biệt rõ rệt so với phần lớn các điểm dữ liệu còn lại – đó chính là dữ liệu ngoại lai (outlier). Những giá trị này có thể do lỗi nhập liệu, yếu tố khách quan đặc biệt, hay đơn giản là những sự kiện hiếm gặp trong thực tế. Việc phát hiện và xử lý đúng cách các outlier đóng vai trò quan trọng trong việc đảm bảo tính chính xác của phân tích dữ liệu và mô hình dự đoán.
Thống kê cho thấy, một Data Analyst dành tới 80% thời gian để làm sạch dữ liệu – và phần lớn trong đó là phát hiện, phân loại và xử lý các giá trị ngoại lai. Một tập dữ liệu sạch giúp kết quả phân tích phản ánh đúng thực tế và hỗ trợ ra quyết định chính xác hơn.
1. Outlier là gì và tại sao cần quan tâm?
Outlier là các giá trị trong tập dữ liệu có sự chênh lệch lớn so với đa số giá trị còn lại. Nói cách khác, đây là những điểm dữ liệu “lạc lõng”, không tuân theo quy luật chung. Nếu không được xử lý, chúng có thể gây sai lệch nghiêm trọng đến giá trị trung bình, phương sai và độ chính xác của các mô hình dự báo.
Tuy nhiên, không phải mọi outlier đều nên bị loại bỏ. Một số giá trị ngoại lai có thể tiết lộ insight giá trị — chẳng hạn như hành vi đặc biệt của khách hàng, sự cố kỹ thuật, hay xu hướng thị trường đột biến.
- Ảnh hưởng tiêu cực: Làm sai lệch mô hình, gây thiên lệch thống kê, giảm độ tin cậy của kết quả phân tích.
- Giá trị tích cực: Cung cấp thông tin hiếm, giúp khám phá nguyên nhân sâu xa hoặc cơ hội mới.
2. Các cách phát hiện dữ liệu ngoại lai (Outlier Detection)
Phát hiện outlier là bước nền tảng trước khi bạn quyết định giữ hay loại bỏ chúng. Dưới đây là các phương pháp phổ biến mà Data Analyst thường sử dụng:
2.1. Quan sát trực tiếp trong bảng dữ liệu
Cách đơn giản nhất là sắp xếp dữ liệu (sort) và kiểm tra bằng mắt. Ví dụ, cột “Tuổi” có giá trị 470 tuổi rõ ràng là lỗi nhập liệu. Phương pháp này chỉ phù hợp với các tập dữ liệu nhỏ vì tốn thời gian và không định lượng được mức độ ngoại lai.
2.2. Dùng biểu đồ trực quan hóa dữ liệu
Trực quan hóa dữ liệu giúp phát hiện các giá trị bất thường nhanh chóng:
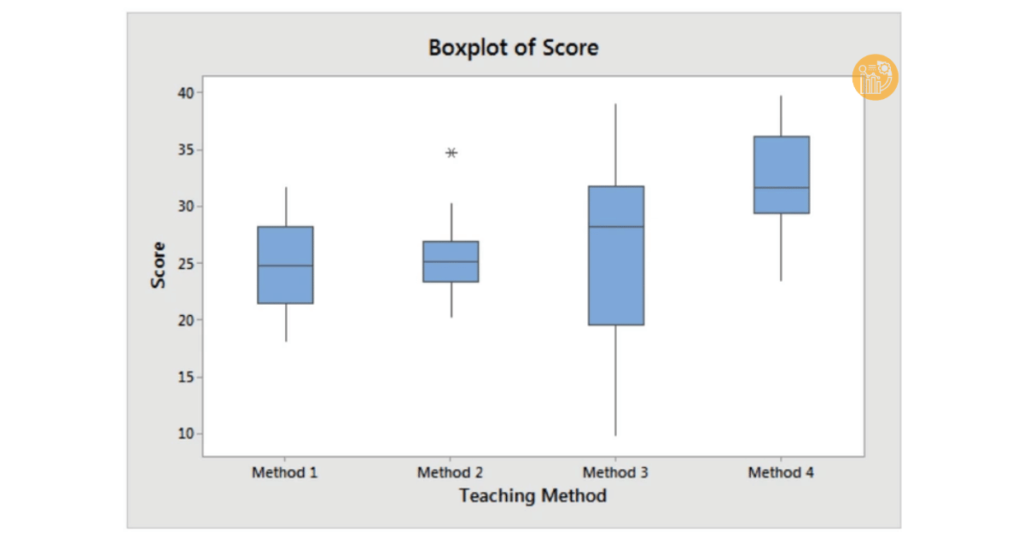
- Boxplot: Hiển thị các giá trị ngoại lai bằng những chấm ở hai đầu biểu đồ.
- Histogram: Các giá trị ngoại lai tách biệt hẳn khỏi phần lớn phân phối dữ liệu.
- Scatter plot: Phát hiện outlier trong phân tích đa biến, những điểm nằm xa khỏi cụm dữ liệu chính.
Ví dụ, trong phân tích thị trường chứng khoán Brazil, cổ phiếu của Petrobras giảm 15,8% trong khi chỉ số chung giảm 8,8% – một giá trị ngoại lai cần được xem xét để hiểu nguyên nhân sâu hơn.
2.3. Phát hiện bằng các phương pháp thống kê
Khi dữ liệu có quy mô lớn, bạn cần các công cụ định lượng để phát hiện outlier chính xác hơn.
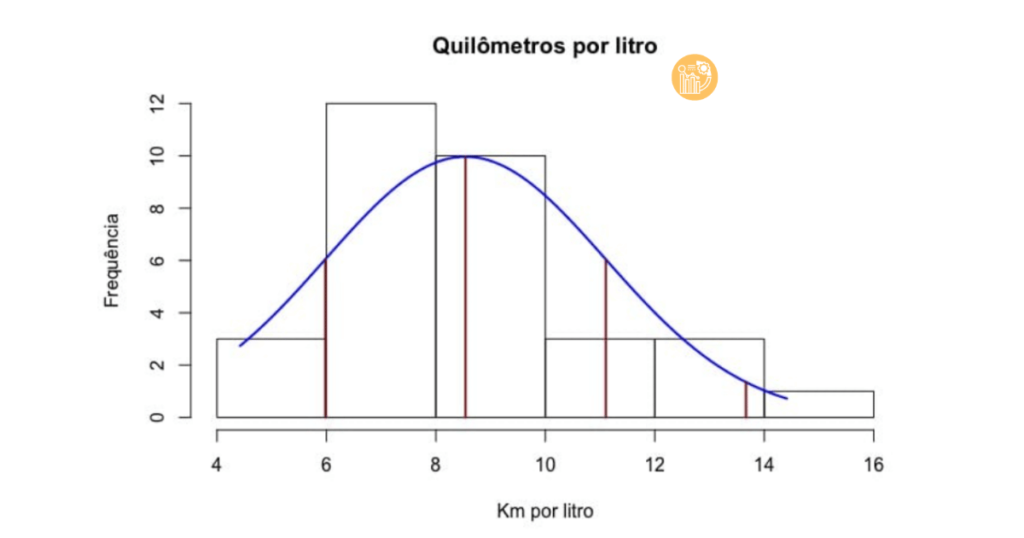
a. Dựa vào giá trị trung bình và độ lệch chuẩn
Trong phân phối chuẩn, khoảng 95% dữ liệu nằm trong phạm vi ±2 độ lệch chuẩn quanh giá trị trung bình. Những điểm vượt ngoài ±2 hoặc ±3 độ lệch chuẩn được coi là ngoại lai. Ví dụ, trong tập dữ liệu về mức tiêu hao nhiên liệu (km/l), những xe có hiệu suất vượt hơn 2 độ lệch chuẩn so với trung bình là các outlier.
b. Sử dụng Z-score
Z-score cho biết một điểm dữ liệu cách giá trị trung bình bao nhiêu độ lệch chuẩn. Nếu |Z| ≥ 3, đó là dấu hiệu rõ ràng của outlier. Công thức tính:
Z = (X – μ) / σ
Z-score càng xa 0, giá trị càng bất thường. Tuy nhiên, phương pháp này chỉ phù hợp khi dữ liệu gần với phân phối chuẩn.
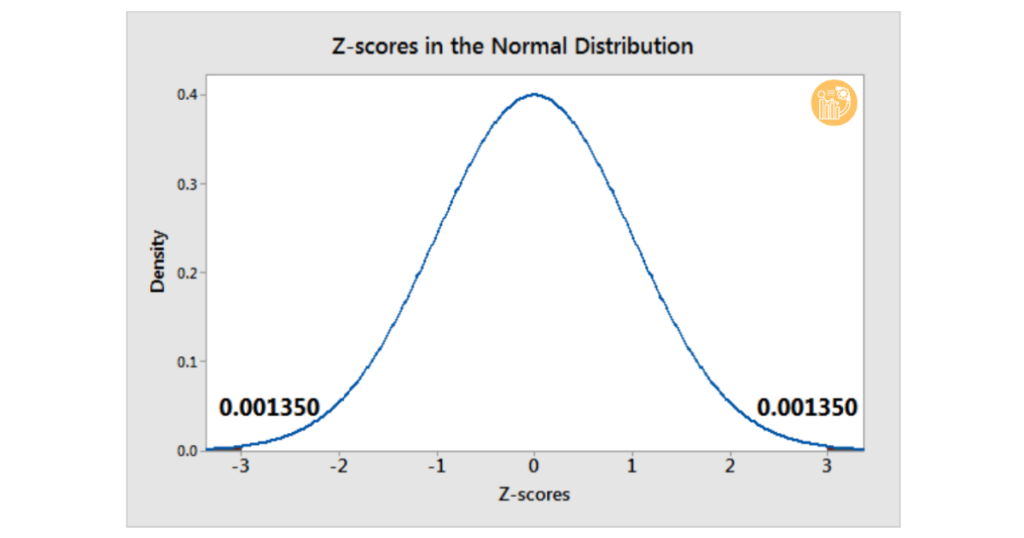
c. Phương pháp Interquartile Range (IQR)
Phương pháp IQR sử dụng phần tư (Q1, Q3) để xác định khoảng giá trị bình thường. Dữ liệu nằm ngoài phạm vi [Q1 – 1.5×IQR, Q3 + 1.5×IQR] được coi là ngoại lai.
Ví dụ: Nếu Q1 = 1.714 và Q3 = 1.936, thì IQR = 0.222. Khi đó:
- Ngưỡng dưới = 1.714 – 1.5×0.222 = 1.381
- Ngưỡng trên = 1.936 + 1.5×0.222 = 2.269
Những giá trị nhỏ hơn 1.381 hoặc lớn hơn 2.269 được xem là outlier. Đây là cách phổ biến nhất do không yêu cầu phân phối chuẩn.

d. Kiểm định giả thuyết (Hypothesis Testing)
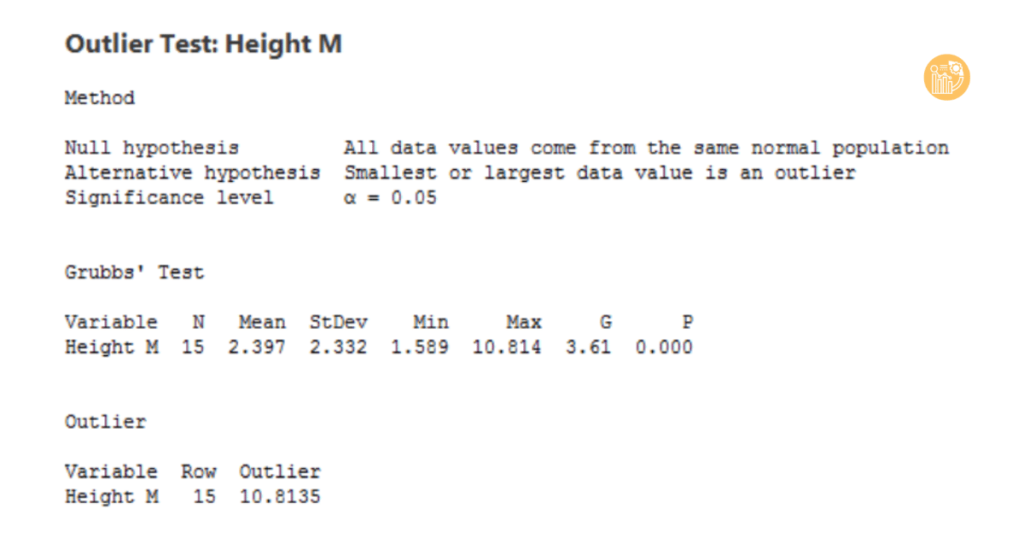
Phương pháp Grubbs’ Test là một trong những kỹ thuật phổ biến nhất. Kiểm định này giúp xác định liệu trong tập dữ liệu có một điểm nằm ngoài phân phối chuẩn hay không.
- H0: Không có giá trị ngoại lai.
- H1: Có ít nhất một giá trị ngoại lai.
Nếu p-value < 0.05, bạn có thể kết luận rằng tồn tại giá trị ngoại lai. Tuy nhiên, cần lưu ý tránh lỗi “masking” (bỏ sót outlier) hoặc “swamping” (phát hiện sai outlier) khi xác định số lượng ngoại lệ cần kiểm tra.
3. Cách xử lý dữ liệu ngoại lai trong phân tích
Sau khi phát hiện, việc tiếp theo là quyết định nên giữ lại hay loại bỏ các outlier. Tùy thuộc vào mục tiêu nghiên cứu và bản chất của dữ liệu, bạn có thể chọn một trong các hướng xử lý sau:
- Loại bỏ giá trị ngoại lai: Khi chắc chắn đó là lỗi nhập liệu hoặc giá trị không đại diện cho hiện tượng cần phân tích.
- Chuyển đổi dữ liệu (Transformation): Áp dụng log, square root hoặc normalization để giảm ảnh hưởng của outlier.
- Thay thế bằng giá trị trung vị (median): Dùng trong các trường hợp giá trị bất thường nhưng không thể loại bỏ hoàn toàn.
- Sử dụng mô hình robust: Các thuật toán như Robust Regression, Decision Tree hoặc Random Forest có khả năng chịu ảnh hưởng của outlier tốt hơn.
- Giữ lại để phân tích chuyên sâu: Khi outlier phản ánh hiện tượng đặc biệt hoặc insight quan trọng (ví dụ: khách hàng VIP, sự cố kỹ thuật bất thường).
4. Khi nào không nên loại bỏ outlier?
Outlier không phải lúc nào cũng là “rác dữ liệu”. Ví dụ, nếu bạn đang phân tích mức lương trong công ty và thấy một giá trị vượt trội gấp 10 lần phần còn lại – có thể đó là mức lương của CEO. Đây là giá trị hợp lệ, phản ánh thực tế và cần được giữ lại để mô hình không mất tính đại diện.
5. Kết luận
Hiểu và xử lý đúng cách dữ liệu ngoại lai giúp Data Analyst đảm bảo độ tin cậy của kết quả phân tích, hạn chế sai lệch thống kê và tăng khả năng dự đoán chính xác. Outlier không chỉ là “nhiễu” mà còn có thể là “tín hiệu” – nếu bạn biết cách khai thác chúng đúng hướng.
Để thành thạo hơn trong việc phân tích và xử lý dữ liệu thực tế, bạn có thể tham khảo khóa học Data Analysis của Tomorrow Marketers – nơi bạn được học cách đọc hiểu, làm sạch và biến dữ liệu thành quyết định kinh doanh có giá trị.