Trong nghiên cứu khoa học và xử lý dữ liệu định lượng, việc phân loại chính xác biến định tính và biến định lượng giữ vai trò vô cùng quan trọng. Đây là bước nền tảng giúp nhà nghiên cứu lựa chọn đúng phương pháp phân tích, đảm bảo kết quả phản ánh đúng bản chất của dữ liệu.

Nếu xác định sai loại biến, ví dụ đưa biến định tính vào chạy các kiểm định yêu cầu biến định lượng như hồi quy tuyến tính hay mô hình SEM, phần mềm vẫn cho ra bảng kết quả. Tuy nhiên, những con số đó hoàn toàn vô nghĩa, không có giá trị khoa học và có thể dẫn đến diễn giải sai lầm, ảnh hưởng trực tiếp đến độ tin cậy của nghiên cứu.

Bài viết này nhằm giải thích một cách rõ ràng và dễ hiểu sự khác biệt giữa biến định tính và biến định lượng, đồng thời đưa ra hướng xử lý phù hợp khi phân tích dữ liệu trên các phần mềm phổ biến như SPSS, SmartPLS và AMOS. Qua đó, người đọc có thể áp dụng đúng loại biến vào các kiểm định, tránh sai sót và nâng cao chất lượng nghiên cứu.

1. Biến định tính (Categorical Variable) là gì?

Khái niệm cơ bản

Biến định tính (Categorical Variable), còn gọi là biến phân loại, là loại biến dùng để chia đối tượng nghiên cứu thành các nhóm hoặc loại khác nhau dựa trên một đặc điểm nhất định. Các giá trị của biến định tính thường biểu diễn thuộc tính chứ không phải con số đo lường thực tế. Vì vậy, biến định tính giúp nhà nghiên cứu phân nhóm đối tượng nhưng không phản ánh mức độ chênh lệch chính xác giữa các nhóm.

Đặc điểm của biến định tính

• Khi xử lý dữ liệu, biến định tính thường được mã hóa bằng số (coding), chẳng hạn 1 = Nam, 2 = Nữ. Tuy nhiên, các con số này chỉ mang tính quy ước để phân biệt nhóm, hoàn toàn không có ý nghĩa định lượng.
• Biến định tính thường không thể dùng trực tiếp cho các phép toán cộng, trừ, nhân, chia, trung bình,… vì bản chất của chúng không phải giá trị số học.
• Trong phân tích dữ liệu, biến định tính thường được dùng cho các thống kê tần suất, bảng chéo, kiểm định Chi-square hoặc làm biến kiểm soát, biến giả (dummy variable) trong hồi quy và SEM.

Ví dụ minh họa

Để dễ hình dung, có thể xem các trường hợp sau:

• Biến độ tuổi nhóm: Thay vì thu thập số tuổi chính xác, nhà nghiên cứu chia thành các nhóm:
  • (1) Dưới 22 tuổi
  • (2) Từ 22–30 tuổi
  • (3) Trên 30 tuổi Con số 1, 2, 3 ở đây chỉ mang tính quy ước phân loại, không phản ánh chênh lệch thực tế giữa các nhóm tuổi.
• Biến giới tính: Thường được mã hóa 1 = Nam, 2 = Nữ. Rõ ràng, số 2 không lớn hơn số 1 về mặt “giới tính”, mà chỉ là mã số để nhận diện nhóm.
• Biến học vấn: Phân loại theo trình độ như 1 = Cao đẳng, 2 = Đại học, 3 = Sau đại học. Các giá trị này không cho thấy “khoảng cách” cụ thể về số năm học giữa các nhóm, mà chỉ giúp phân loại theo cấp bậc học vấn.

Xem thêm: Các loại biến trong phân tích dữ liệu định lượng (P2: Biến định tính)

2. Biến định lượng (Quantitative Variable) là gì?

Khái niệm cơ bản

Biến định lượng (Quantitative Variable) là loại biến mà giá trị của nó được biểu diễn bằng con số thực và phản ánh trực tiếp một đại lượng đo lường cụ thể. Khác với biến định tính chỉ dùng để phân loại, biến định lượng cho phép người nghiên cứu đo lường, tính toán và so sánh giữa các đối tượng nghiên cứu dựa trên giá trị số học. Đây là loại biến đóng vai trò then chốt trong các phân tích thống kê, hồi quy, và mô hình SEM.

Đặc điểm của biến định lượng

• Các giá trị của biến định lượng có ý nghĩa toán học, do đó có thể áp dụng trực tiếp các phép tính như cộng, trừ, nhân, chia, tính trung bình, phương sai, độ lệch chuẩn,…
• Biến định lượng có khả năng phản ánh sự khác biệt về mức độ giữa các đối tượng. Ví dụ, người 30 tuổi nhiều hơn người 25 tuổi 5 năm; thu nhập 15 triệu cao hơn thu nhập 10 triệu 5 triệu đồng.
• Loại biến này được sử dụng phổ biến trong hầu hết các phương pháp phân tích định lượng như: kiểm định T-test, ANOVA, hồi quy tuyến tính, phân tích nhân tố (EFA/CFA), và mô hình cấu trúc SEM.

Ví dụ minh họa

Một số ví dụ điển hình giúp phân biệt rõ biến định lượng:

• Biến độ tuổi: Nếu dữ liệu thu thập số tuổi thật của đáp viên, chẳng hạn 23, 25, 30… thì đây là biến định lượng, vì giá trị phản ánh chính xác số năm tuổi.
• Biến thu nhập: Nếu dữ liệu được ghi nhận ở dạng con số thực, ví dụ 10.000.000đ, 12.500.000đ, 20.000.000đ, thì đó là biến định lượng. Các con số này mang ý nghĩa đo lường thực tế và có thể tính toán các chỉ số thống kê.
• Biến số năm kinh nghiệm làm việc: Với dữ liệu thu thập trực tiếp số năm, ví dụ 3 năm, 7 năm, 12 năm, ta có biến định lượng thể hiện chính xác thời gian làm việc của từng cá nhân.

Như vậy, biến định lượng cung cấp nền tảng cho việc phân tích dữ liệu chuyên sâu, vì nó cho phép áp dụng các phương pháp thống kê phức tạp và đưa ra kết quả định lượng có giá trị khoa học.

Xem thêm: Các loại biến trong phân tích dữ liệu định lượng (P1: Biến định lượng)

3. So sánh biến định tính và biến định lượng

Sau khi đã hiểu rõ khái niệm của biến định tính (Categorical Variable) và biến định lượng (Quantitative Variable), bước tiếp theo quan trọng là phân biệt sự khác nhau giữa hai loại biến này. Việc nắm rõ điểm khác biệt không chỉ giúp thiết kế bảng hỏi khoa học mà còn đảm bảo chọn đúng phương pháp phân tích dữ liệu trong SPSS, AMOS hay SmartPLS.

Tiêu chí phân biệt

Có thể phân biệt biến định tính và biến định lượng dựa trên các tiêu chí sau:

Tiêu chí	Biến định tính (Categorical Variable)	Biến định lượng (Quantitative Variable)
Khái niệm	Biến dùng để phân loại đối tượng thành các nhóm dựa trên thuộc tính hoặc đặc điểm.	Biến thể hiện bằng con số thực, phản ánh giá trị đo lường cụ thể.
Bản chất dữ liệu	Mang tính phân loại, các giá trị thường là ký hiệu hoặc số quy ước.	Mang tính đo lường, giá trị là con số thực có ý nghĩa.
Khả năng tính toán	Không thể thực hiện các phép toán số học như cộng, trừ, trung bình.	Có thể thực hiện phép toán số học (cộng, trừ, trung bình, phương sai, độ lệch chuẩn).
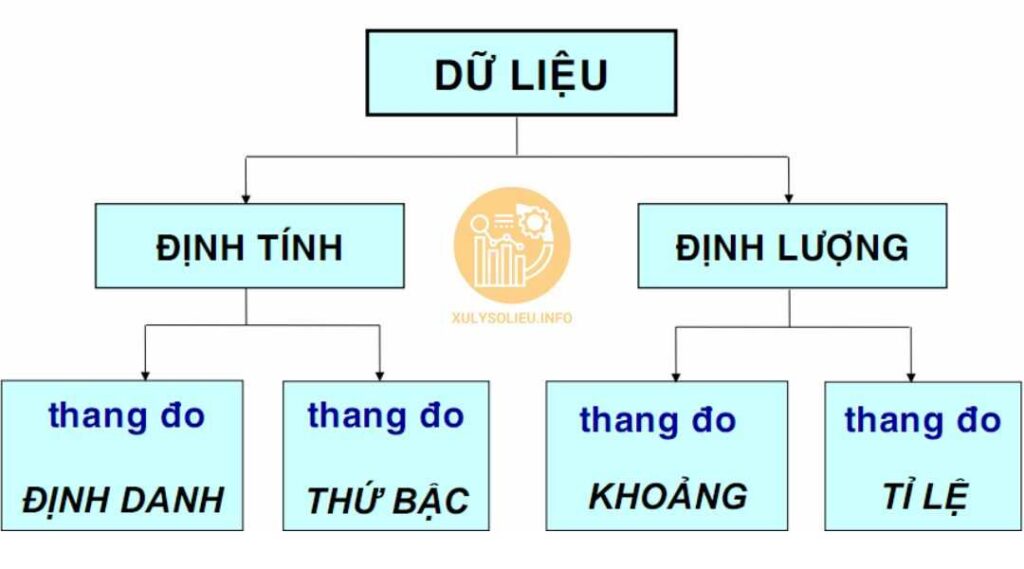
Thang đo	Nominal (danh mục) và Ordinal (thứ bậc).	Interval (khoảng) và Ratio (tỷ lệ).
Ví dụ	Giới tính (Nam/Nữ), Nhóm tuổi (dưới 22, 22–30, trên 30), Trình độ học vấn.	Tuổi thật (23, 25, 30), Thu nhập (10 triệu, 12.5 triệu), Số năm kinh nghiệm (5 năm, 10 năm).
Ứng dụng phân tích	Thống kê tần suất, bảng chéo, Chi-square, ANOVA (khi so sánh với biến định lượng).	Hồi quy tuyến tính, phân tích nhân tố, SEM, kiểm định T-test, phân tích tương quan.
Mã hóa dữ liệu	Thường phải mã hóa (1, 2, 3…), nhưng chỉ mang tính quy ước.	Giữ nguyên số liệu thực, không cần mã hóa.

Lưu ý trong phân tích dữ liệu

• Sai lầm phổ biến: Nhiều sinh viên khi xử lý dữ liệu thường nhầm lẫn, đưa biến định tính vào các phép phân tích yêu cầu dữ liệu định lượng. Phần mềm vẫn cho kết quả nhưng các con số này không có ý nghĩa khoa học.
• Cách khắc phục:
  • Luôn xác định loại biến trước khi phân tích.
  • Nếu muốn đưa biến định tính vào hồi quy hoặc SEM, cần chuyển thành biến giả (dummy variable).
  • Với các biến thứ bậc (ordinal), cần cân nhắc kỹ việc xử lý: giữ ở dạng định tính hay quy đổi thành thang đo định lượng.

Ý nghĩa của việc phân biệt

• Đảm bảo lựa chọn kiểm định phù hợp với dữ liệu đầu vào.
• Nâng cao tính chính xác, độ tin cậy của kết quả nghiên cứu.
• Tránh tình trạng báo cáo kết quả sai lệch do xử lý nhầm loại biến.

4. Một số lưu ý quan trọng khi xử lý dữ liệu

Trong quá trình phân tích dữ liệu, việc phân loại biến định tính và biến định lượng đôi khi không đơn giản như tên gọi của chúng. Nhiều biến có thể được coi là định tính hoặc định lượng tùy theo cách thu thập dữ liệu và mục đích nghiên cứu. Nếu không xác định chính xác, người nghiên cứu có thể lựa chọn sai phương pháp kiểm định, dẫn đến kết quả thiếu ý nghĩa. Dưới đây là một số lưu ý quan trọng cần nắm rõ.

Một biến có thể là định tính hoặc định lượng tùy cách thu thập

Không phải biến nào cũng “mặc định” thuộc nhóm định tính hoặc định lượng. Cách bạn thiết kế bảng hỏi và thu thập dữ liệu mới quyết định bản chất của biến đó.

• Ví dụ với biến độ tuổi:
  • Nếu hỏi số tuổi thật (23, 25, 30…), dữ liệu thu được là số đo cụ thể, vì vậy đây là biến định lượng.
  • Nếu chia thành nhóm tuổi (dưới 22, 22–30, trên 30), dữ liệu mang tính phân loại, do đó là biến định tính.
• Ví dụ với biến thu nhập:
  • Nếu thu thập số tiền chính xác (10 triệu, 12.5 triệu, 20 triệu…), đây là biến định lượng.
  • Nếu chia thành nhóm (dưới 10 triệu, 11–20 triệu, 21–30 triệu…), dữ liệu này chỉ dùng để phân loại, nên là biến định tính.
• Ví dụ với biến học vấn:
  • Nếu đo bằng số năm đi học (12 năm, 15 năm…), đây là biến định lượng.
  • Nếu phân loại thành bậc học vấn (trung cấp, đại học, sau đại học), đây là biến định tính.

Điều này cho thấy bản chất biến phụ thuộc rất nhiều vào cách thiết kế thang đo và mục tiêu nghiên cứu.

Biến có hai giá trị có thể dùng như định lượng

Một số biến có hai giá trị (binary variable) thường được coi là biến định tính. Tuy nhiên, trong nhiều trường hợp, chúng hoàn toàn có thể xử lý như biến định lượng để đưa vào hồi quy hoặc SEM.

• Ví dụ biến giới tính: Nếu chỉ gồm hai nhóm Nam/Nữ, biến này có thể được mã hóa thành 0 và 1. Khi đó, biến vừa có tính phân loại, vừa có thể sử dụng trong các mô hình định lượng.
• Ví dụ biến quyết định mua hàng: (Có = 1, Không = 0). Đây là biến nhị phân, thường được sử dụng trực tiếp trong các mô hình hồi quy logistic hoặc SEM.

Do đó, biến hai giá trị có tính linh hoạt cao, tùy thuộc vào phương pháp phân tích mà có thể coi là định tính hoặc định lượng.

Đừng nhầm lẫn tên biến với loại biến

Một sai lầm phổ biến là xác định loại biến dựa vào tên gọi, thay vì dữ liệu thực tế.

• Ví dụ biến “Thu nhập”: Nếu thu thập số tiền thực, nó là định lượng. Nhưng nếu chia thành nhóm thu nhập, nó lại trở thành định tính.
• Ví dụ biến “Độ tuổi”: Cùng tên gọi nhưng có thể là định tính (nếu chia nhóm) hoặc định lượng (nếu thu số tuổi thật).

Điều quan trọng cần nhớ là: loại biến được quyết định bởi dữ liệu và cách thu thập, không phải bởi tên gọi trong bảng hỏi hay file dữ liệu.

5. Kỹ thuật chuyển đổi biến định tính sang định lượng

Trong nhiều phân tích thống kê như hồi quy tuyến tính, hồi quy logistic hay mô hình SEM, đầu vào thường yêu cầu biến định lượng. Điều này dẫn đến khó khăn khi nhà nghiên cứu muốn đưa biến định tính (ví dụ: giới tính, học vấn, phòng ban, khu vực…) vào mô hình. Giải pháp phổ biến là sử dụng biến giả (dummy variable) để chuyển đổi.

Khái niệm biến giả (Dummy Variable)

Biến giả là biến định lượng được tạo ra từ một biến định tính nhằm mã hóa thông tin nhóm/loại của biến đó thành dạng 0 hoặc 1.

• 0: không thuộc nhóm.
• 1: thuộc nhóm.

Nhờ vậy, biến định tính có thể tham gia vào các phép phân tích yêu cầu dữ liệu định lượng.

Cách tạo biến giả

Giả sử bạn có một biến định tính “Trình độ học vấn” với 4 nhóm:

• Trung cấp
• Cao đẳng
• Đại học
• Sau đại học

Để đưa biến này vào hồi quy, bạn cần tạo 3 biến giả (luôn ít hơn số nhóm một đơn vị, để tránh hiện tượng đa cộng tuyến):

• Dummy 1 (Cao đẳng): 1 = Cao đẳng, 0 = nhóm khác.
• Dummy 2 (Đại học): 1 = Đại học, 0 = nhóm khác.
• Dummy 3 (Sau đại học): 1 = Sau đại học, 0 = nhóm khác.

Nhóm còn lại (Trung cấp) sẽ được coi là nhóm tham chiếu (reference group).

Ưu và nhược điểm của biến giả

Ưu điểm:

• Cho phép đưa biến định tính vào mô hình định lượng.
• Dễ tạo và dễ diễn giải khi chỉ có vài nhóm.
• Phổ biến trong hầu hết các phần mềm (SPSS, Stata, R, SmartPLS).

Nhược điểm:

• Nếu biến định tính có quá nhiều nhóm (ví dụ 10 nhóm trở lên), việc tạo biến giả sẽ làm tăng số lượng biến, dẫn đến mô hình phức tạp.
• Diễn giải kết quả trở nên khó khăn hơn nếu có nhiều biến giả cùng lúc.

Ứng dụng trong hồi quy và SEM

• Hồi quy tuyến tính (SPSS, Stata): Biến giả được đưa vào như biến độc lập. Hệ số hồi quy thể hiện mức chênh lệch so với nhóm tham chiếu.
• SEM (AMOS, SmartPLS): Trước khi đưa vào mô hình, biến định tính thường được chuyển đổi thành dummy để đảm bảo tính đúng đắn về mặt dữ liệu.
• Hồi quy logistic: Các biến nhị phân (có/không, nam/nữ) vốn dĩ đã ở dạng dummy nên có thể sử dụng trực tiếp.

Ví dụ minh họa

Giả sử biến Giới tính với hai giá trị: Nam, Nữ.

• Nếu mã hóa: Nam = 0, Nữ = 1, thì biến giới tính đã trở thành dummy variable.
• Khi đưa vào hồi quy với biến phụ thuộc là mức độ hài lòng, hệ số hồi quy của giới tính sẽ cho biết sự khác biệt trung bình về mức độ hài lòng giữa nam và nữ.

6. Kết luận

Việc xác định đúng loại biến – định tính hay định lượng – là bước nền tảng trong phân tích dữ liệu. Nếu phân loại sai, bạn không chỉ gặp lỗi khi chọn kiểm định mà còn có thể diễn giải sai kết quả, làm giảm độ tin cậy và giá trị khoa học của nghiên cứu.

Trước khi đưa bất kỳ biến nào vào phân tích, bạn cần trả lời rõ ràng hai câu hỏi:

• Dữ liệu đang thu thập là giá trị số thực (có thể đo lường) hay chỉ là dạng phân loại?
• Kiểm định thống kê hoặc mô hình phân tích mà bạn lựa chọn yêu cầu biến đầu vào phải là định tính hay định lượng?

Một khi đã phân biệt chính xác, bạn sẽ dễ dàng chọn được phương pháp phân tích phù hợp, đảm bảo kết quả có ý nghĩa và phản ánh đúng bản chất dữ liệu.

Nếu bạn gặp khó khăn trong quá trình xử lý dữ liệu, đặc biệt là:

• Phân loại biến định tính – định lượng,
• Chuyển đổi biến định tính thành biến giả để đưa vào hồi quy hoặc SEM,
• Tư vấn lựa chọn và chạy kiểm định phù hợp trong SPSS, AMOS hay SmartPLS,

Hãy liên hệ ngay đội ngũ chuyên gia của chúng tôi để nhận được hỗ trợ chi tiết và các giải pháp tối ưu cho nghiên cứu của bạn.

Liên hệ ngay: https://xulysolieu.info/lien-he/