Độ lệch chuẩn là một trong những khái niệm quan trọng nhất trong thống kê, giúp chúng ta đo lường mức độ phân tán của dữ liệu xung quanh giá trị trung bình. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về công thức tính độ lệch chuẩn, mối quan hệ giữa độ lệch chuẩn và phương sai, cũng như các ví dụ minh họa để giúp bạn dễ dàng hiểu và áp dụng.
Mục lục
ToggleKhái Niệm Độ Lệch Chuẩn
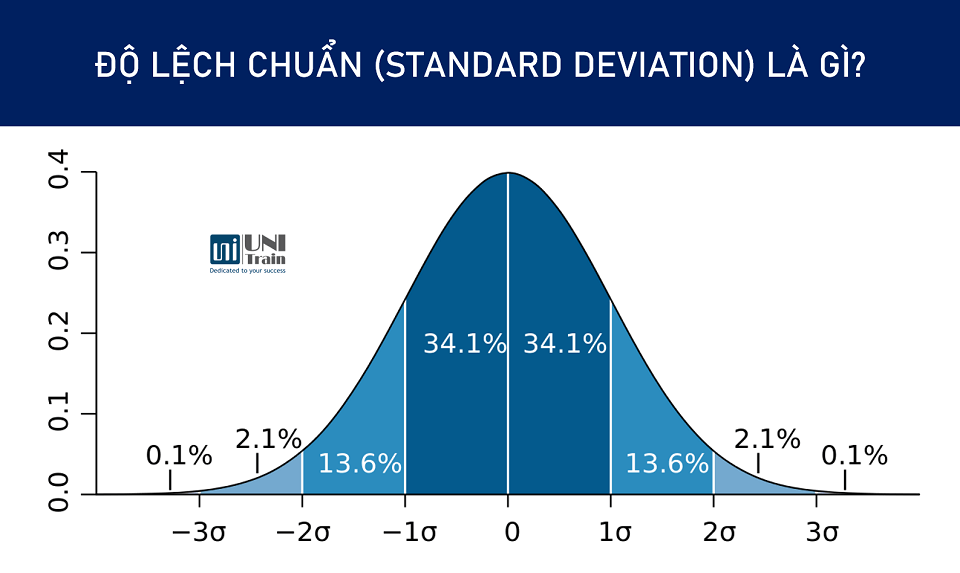
Độ lệch chuẩn (Standard Deviation) là đại lượng thống kê đo lường mức độ phân tán của dữ liệu xung quanh trung bình. Nó cho biết trung bình mỗi điểm dữ liệu cách xa trung bình bao nhiêu đơn vị.
Ví dụ:
- Nếu độ lệch chuẩn của điểm số của học sinh trong một lớp học là 5 điểm, điều đó có nghĩa là trung bình mỗi học sinh có điểm số lệch 5 điểm so với điểm trung bình của lớp.
- Nếu độ lệch chuẩn của chiều cao của người dân trong một vùng là 10cm, điều đó có nghĩa là trung bình mỗi người có chiều cao lệch 10cm so với chiều cao trung bình của người dân trong vùng.
Vai Trò của Độ Lệch Chuẩn
Độ lệch chuẩn đóng vai trò quan trọng trong nhiều lĩnh vực, bao gồm:
- Phân tích dữ liệu: Giúp đánh giá mức độ phân tán của dữ liệu, cho phép nhà nghiên cứu đưa ra kết luận chính xác hơn.
- Kiểm tra giả thuyết: Được sử dụng để xác định xem sự khác biệt giữa hai nhóm dữ liệu có ý nghĩa thống kê hay không.
- Dự báo: Được dùng để dự báo tương lai, ví dụ như dự báo doanh thu của một công ty.
- Kiểm soát chất lượng: Được dùng để kiểm soát chất lượng sản phẩm, ví dụ kiểm tra kích thước sản phẩm có đạt tiêu chuẩn hay không.
Công Thức Tính Độ Lệch Chuẩn
Có hai công thức tính độ lệch chuẩn, tùy thuộc vào việc bạn đang làm việc với một mẫu dữ liệu hay toàn bộ quần thể.
1. Công Thức Tính Độ Lệch Chuẩn Mẫu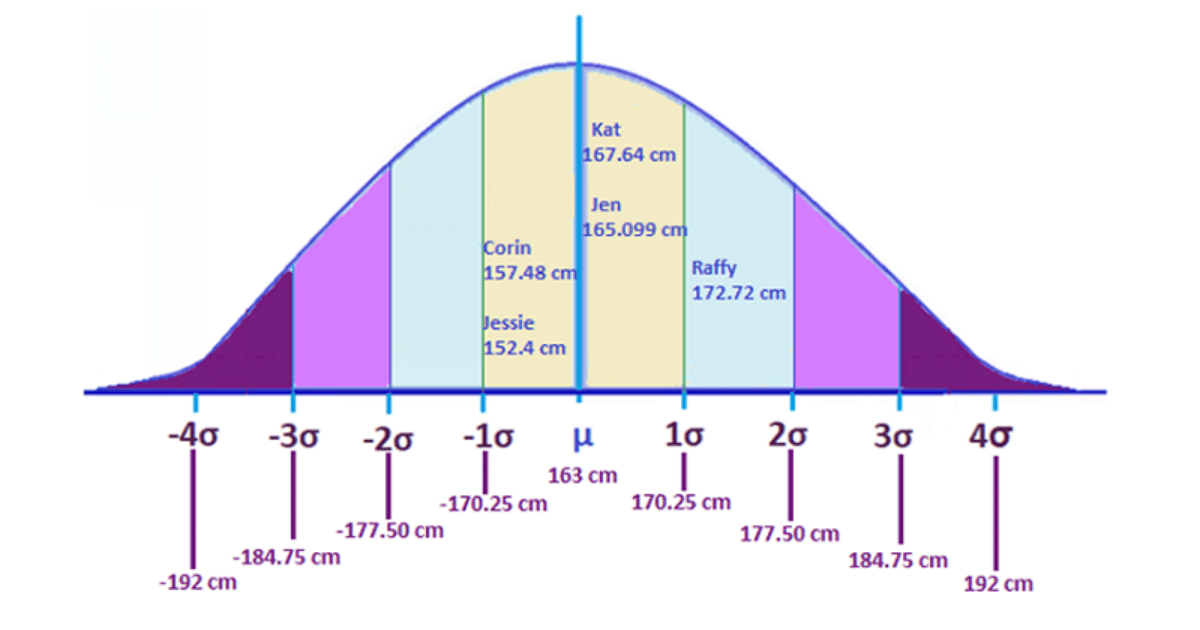
Công thức tính độ lệch chuẩn mẫu được sử dụng khi bạn chỉ có một mẫu con của dữ liệu:
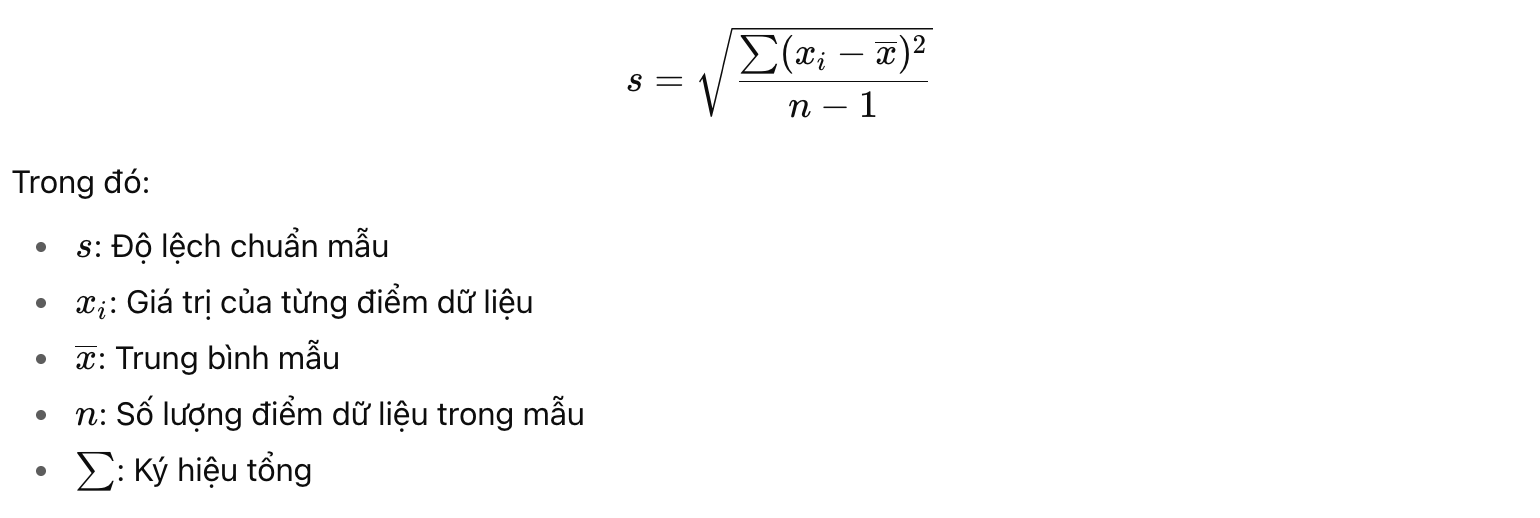
Công thức này sử dụng n−1n – 1n−1 để điều chỉnh độ lệch chuẩn mẫu cho phù hợp với độ lệch chuẩn của tổng thể.
2. Công Thức Tính Độ Lệch Chuẩn Quần Thể
Khi bạn có toàn bộ dữ liệu của quần thể, công thức tính độ lệch chuẩn là:
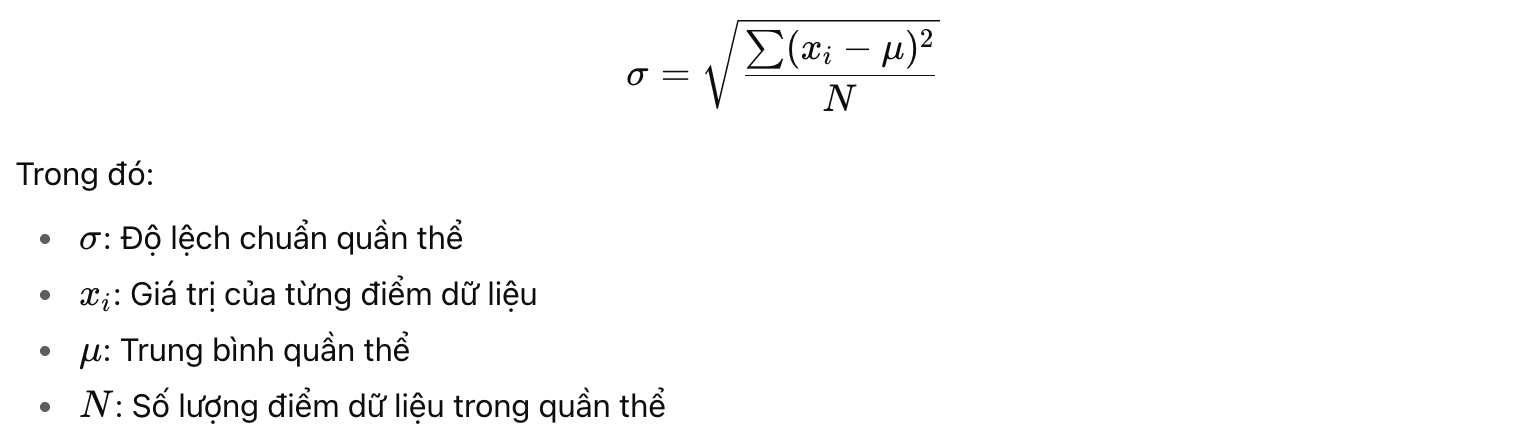
Lưu ý: Công thức tính độ lệch chuẩn quần thể không sử dụng n−1n – 1n−1 mà dùng NNN vì bạn có toàn bộ dữ liệu của quần thể.
Mối Quan Hệ Giữa Độ Lệch Chuẩn và Phương Sai
Phương sai và độ lệch chuẩn có mối quan hệ mật thiết. Phương sai (Variance) là bình phương của độ lệch chuẩn và đo lường mức độ phân tán của dữ liệu so với trung bình.
Công Thức Tính Phương Sai
- Phương sai mẫu:
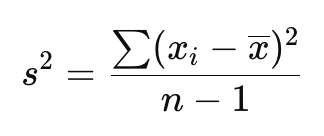
- Phương sai quần thể:
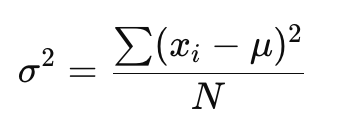
Mối Quan Hệ
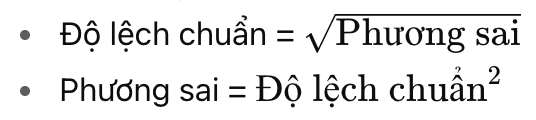
Ví dụ: Nếu độ lệch chuẩn của một tập dữ liệu là 3, phương sai của nó sẽ là 9 (3² = 9).
Lợi Ích Của Việc Sử Dụng Độ Lệch Chuẩn Thay Vì Phương Sai
- Đơn vị dễ hiểu: Độ lệch chuẩn có đơn vị giống với dữ liệu gốc, trong khi phương sai có đơn vị là bình phương của dữ liệu.
- Dễ hình dung hơn: Độ lệch chuẩn giúp dễ dàng hiểu được mức độ phân tán của dữ liệu theo đơn vị dữ liệu ban đầu.
Ví dụ: Nếu đơn vị dữ liệu là mét, thì độ lệch chuẩn cũng có đơn vị là mét. Trong khi đó, phương sai sẽ có đơn vị là mét vuông.
Ví Dụ Minh Họa
Giả sử bạn có tập hợp dữ liệu sau: 1,2,3,4,5
Bước 1: Tính Trung Bình Mẫu
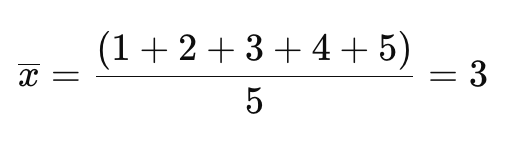
Bước 2: Tính Phương Sai
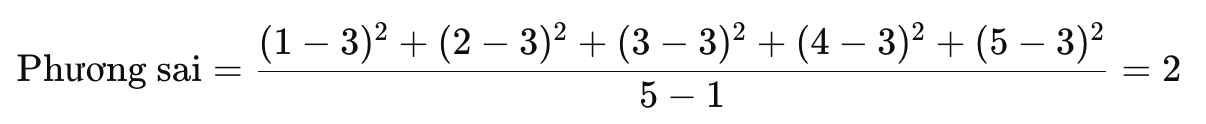
Bước 3: Tính Độ Lệch Chuẩn
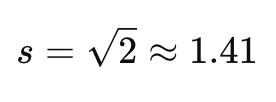
Kết luận: Độ lệch chuẩn của tập dữ liệu là 1.41, nghĩa là trung bình mỗi giá trị cách trung bình 1.41 đơn vị.
Tổng Bình Phương Chênh Lệch Là Gì?
Tổng bình phương chênh lệch (TBCCH) là tổng các bình phương chênh lệch giữa mỗi giá trị dữ liệu và trung bình. Nó là cơ sở để tính phương sai và độ lệch chuẩn.
Sự Khác Biệt Giữa Công Thức Quần Thể và Mẫu
| Công Thức | Công Thức Mẫu | Công Thức Quần Thể |
|---|---|---|
| Độ lệch chuẩn | 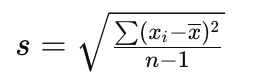 |
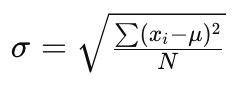 |
| Sử dụng | Mẫu nhỏ từ quần thể lớn | Dữ liệu đầy đủ của quần thể |
| Công thức | Điều chỉnh bằng n−1n – 1n−1 để giảm sai lệch ước lượng | Không cần điều chỉnh, sử dụng NNN |
Kết Luận
Hiểu rõ về công thức tính độ lệch chuẩn và phương sai giúp bạn phân tích dữ liệu một cách chính xác và dễ dàng đưa ra kết luận trong các nghiên cứu hoặc quyết định kinh doanh. Độ lệch chuẩn có vai trò quan trọng trong việc đo lường sự phân tán và đánh giá tính ổn định của dữ liệu. Việc lựa chọn sử dụng độ lệch chuẩn hay phương sai phụ thuộc vào ngữ cảnh và mục đích phân tích.














