Trong quá trình làm việc với SPSS để phân tích dữ liệu, việc hiểu rõ về tương quan và hồi quy là rất quan trọng. Chúng ta hãy cùng tìm hiểu sâu hơn về hai khái niệm này.
Tương quan và hồi quy đều là các kỹ thuật phân tích để xem xét mối quan hệ giữa các biến, nhưng mục đích và cách tiếp cận của chúng lại khác nhau.
Trong bài viết này, xulysolieu.info sẽ giải thích một cách dễ hiểu về tương quan và hồi quy, đồng thời chỉ ra những điểm giống và khác nhau giữa chúng.
Tổng Quan Tương Quan và Hồi Quy trong SPSS
Tương Quan là Gì? (Correlation)
Hệ số tương quan là một chỉ số đo lường mức độ liên kết tuyến tính giữa hai biến số, thường được ký hiệu là x và y. Giá trị của hệ số tương quan nằm trong khoảng từ -1 đến +1.
- Giá trị -1: Biểu thị mối tương quan tuyến tính nghịch biến hoàn hảo. Khi x tăng, y giảm một cách tuyến tính.
- Giá trị 0: Cho thấy không có mối tương quan tuyến tính nào giữa hai biến. Sự thay đổi của một biến không ảnh hưởng đến biến còn lại theo cách tuyến tính.
- Giá trị 1: Biểu thị mối tương quan tuyến tính đồng biến hoàn hảo. Khi x tăng, y cũng tăng một cách tuyến tính.
Ví dụ minh họa:
Xét một tập dữ liệu gồm 15 sinh viên với hai biến: (1) Số giờ học và (2) Điểm thi.
| Số giờ học | Điểm thi |
|---|---|
| 1 | 60 |
| 1 | 63 |
| 2 | 64 |
| 2 | 69 |
| 2 | 65 |
| 3 | 75 |
| 4 | 79 |
| 4 | 73 |
| 5 | 76 |
| 6 | 80 |
| 7 | 83 |
| 7 | 83 |
| 8 | 86 |
| 8 | 85 |
| 9 | 88 |
| 10 | 90 |
| 10 | 87 |
| 11 | 98 |
| 12 | 95 |
Nếu chúng ta biểu diễn mối quan hệ này bằng biểu đồ phân tán (scatterplot), kết quả sẽ như sau:
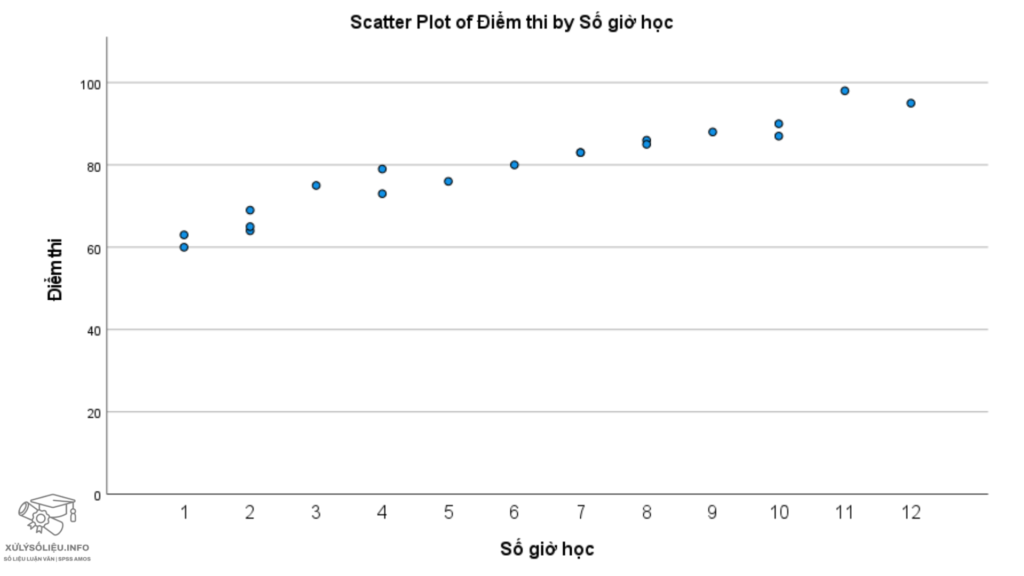Chú thích: Biểu đồ phân tán thể hiện mối quan hệ giữa số giờ học và điểm thi
Biểu đồ này cho thấy có một mối liên hệ tuyến tính dương giữa số giờ học (biến độc lập) và điểm thi (biến phụ thuộc). Điểm thi có xu hướng tăng khi số giờ học tăng.
Khi tính toán tương quan, ta thu được hệ số tương quan r = 0.969. Giá trị này gần bằng 1, khẳng định rằng có một mối tương quan dương mạnh giữa hai biến.
Hồi Quy là Gì? (Regression)
Hồi quy là một phương pháp thống kê dùng để xác định sự ảnh hưởng của biến độc lập (x) lên biến phụ thuộc (y). Nói cách khác, hồi quy giúp ta dự đoán giá trị của một biến dựa trên giá trị của biến khác.
Mô hình hồi quy sử dụng biến x như biến dự báo và biến y như biến phản hồi. Phương trình hồi quy mô tả mối quan hệ giữa hai biến như sau:
y = b0 + b1 * x
Trong đó:
- y: Giá trị dự đoán của biến phản hồi.
- b0: Giao điểm với trục y (giá trị của y khi x = 0).
- b1: Hệ số hồi quy (mức tăng trung bình của y khi x tăng một đơn vị).
- x: Giá trị của biến dự báo.
Ví dụ:
Tiếp tục sử dụng dữ liệu về số giờ học và điểm thi.
Sau khi thực hiện phân tích hồi quy tuyến tính, ta có phương trình hồi quy như sau:
Điểm thi dự kiến = 61.148 + 3.011 (Số giờ học)*
Điều này có nghĩa là:
- Một sinh viên không học giờ nào (0 giờ) dự kiến đạt 61.148 điểm.
- Điểm thi trung bình tăng thêm 3.011 điểm cho mỗi giờ học.
Chúng ta có thể dùng phương trình này để dự đoán điểm thi dựa trên số giờ học. Ví dụ, nếu một sinh viên học 6 giờ, điểm thi dự kiến là:
Điểm thi dự kiến = 61.148 + 3.011 (6) = 79.214*
Phương trình hồi quy có thể được biểu diễn bằng một đường thẳng trên biểu đồ phân tán:
Đường hồi quy cho thấy sự liên hệ giữa hai biến một cách trực quan.
Giá trị hệ số tương quan r = 0.969, khi bình phương lên, ta được r^2 (hệ số xác định). Trong ví dụ này, r^2 = 0.969^2 = 0.939, tức là 93.9% sự biến thiên của điểm thi có thể được giải thích bởi số giờ học.
So Sánh Tương Quan và Hồi Quy
| Tương Quan (Correlation) | Hồi Quy (Regression) |
|---|---|
| Đều định lượng chiều hướng của mối quan hệ giữa hai biến. | |
| Đều đo lường mức độ mạnh yếu của mối quan hệ giữa hai biến. | |
| Không thể hiện mối quan hệ nhân quả. | Có thể cho thấy mối quan hệ nhân quả giữa hai biến (nếu có bằng chứng ủng hộ). |
| Không sử dụng để dự đoán giá trị của một biến dựa trên giá trị của biến khác. | Có thể sử dụng phương trình để dự đoán giá trị của một biến dựa trên giá trị của biến kia. |
| Sử dụng một con số duy nhất (hệ số tương quan). | Sử dụng phương trình để mô tả mối quan hệ giữa hai biến. |
Phân tích tương quan và phân tích hồi quy đều quan trọng trong quá trình phân tích dữ liệu. Nếu bạn gặp khó khăn, hãy tham khảo Dịch vụ chạy SPSS của chúng tôi. Hoặc liên hệ trực tiếp qua fanpage chính thức của xulysolieu.info.
