Phân tích ANOVA (phương sai) là một phương pháp thống kê được sử dụng để kiểm tra sự khác biệt giữa các trung bình của ba nhóm trở lên. ANOVA cho phép bạn so sánh các trung bình số học của các nhóm cùng một lúc, giúp xác định liệu sự khác biệt quan sát được có phải do ngẫu nhiên hay là sự khác biệt thật sự và có ý nghĩa.
- ANOVA một chiều (One-Way ANOVA): Sử dụng một biến độc lập để kiểm tra sự khác biệt giữa các nhóm.
- ANOVA hai chiều (Two-Way ANOVA): Sử dụng hai biến độc lập để kiểm tra sự ảnh hưởng của cả hai yếu tố và sự tương tác giữa chúng đối với biến phụ thuộc.
Mục lục
ToggleKhám phá Phân Tích ANOVA (Phương Sai)
Phương pháp ANOVA rất đa dạng và được ứng dụng trong nhiều lĩnh vực khác nhau, từ nghiên cứu y tế kiểm tra hiệu quả điều trị, đến nghiên cứu thị trường so sánh sở thích của người tiêu dùng. ANOVA đã trở thành một công cụ không thể thiếu để hiểu các hệ thống phức tạp và đưa ra quyết định dựa trên dữ liệu.
Các Điểm Cần Lưu Ý
- ANOVA giúp so sánh trung bình của ba nhóm trở lên để xác định xem sự khác biệt có phải do ngẫu nhiên hay không.
- ANOVA một chiều sử dụng một yếu tố độc lập, trong khi ANOVA hai chiều sử dụng hai yếu tố độc lập và kiểm tra sự tương tác giữa chúng.
- ANOVA phân tách tổng phương sai thành các thành phần khác nhau, giúp phân tích mối quan hệ giữa các biến và xác định sự khác biệt có ý nghĩa.
Cách ANOVA Hoạt Động
Phương pháp ANOVA so sánh các trung bình của các nhóm và xác định xem sự khác biệt giữa các nhóm có ý nghĩa thống kê hay không. ANOVA thường được sử dụng khi dữ liệu là thử nghiệm và tuân theo phân phối chuẩn. Khác với t-test chỉ so sánh hai nhóm, ANOVA có thể xử lý nhiều nhóm cùng lúc, giúp giảm thiểu khả năng mắc lỗi Type I.
- ANOVA một chiều: Sử dụng khi có một biến độc lập và một biến phụ thuộc, giúp so sánh trung bình của ba nhóm trở lên.
- ANOVA hai chiều: Sử dụng khi có hai biến độc lập, giúp phân tích không chỉ tác động riêng lẻ của mỗi yếu tố mà còn xét đến sự tương tác giữa hai yếu tố này đối với biến phụ thuộc.
Ứng Dụng Của ANOVA
ANOVA được sử dụng trong nhiều lĩnh vực để phân tích sự khác biệt giữa các nhóm. Một số ví dụ bao gồm:
- Nghiên cứu y tế: Kiểm tra hiệu quả của các phương pháp điều trị khác nhau.
- Marketing: So sánh sở thích của người tiêu dùng đối với các sản phẩm khác nhau.
- Giáo dục: Phân tích hiệu quả của các phương pháp giảng dạy khác nhau.
- Kinh doanh: Đánh giá hiệu quả của các chiến lược khác nhau trong công ty.
Công Thức ANOVA
Công thức cơ bản của ANOVA là tính toán hệ số F-statistic, được tính bằng tỉ lệ giữa Mean Sum of Squares due to Treatment (MST) và Mean Sum of Squares due to Error (MSE).
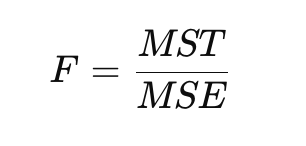
Trong đó:
- MST (Mean Sum of Squares for Treatment) là phương sai giữa các nhóm.
- MSE (Mean Sum of Squares for Error) là phương sai trong mỗi nhóm.
ANOVA Một Chiều vs ANOVA Hai Chiều

ANOVA Một Chiều
- Biến độc lập: Một biến phân loại.
- Biến phụ thuộc: Một biến liên tục.
- Mục đích: So sánh trung bình giữa ba nhóm trở lên.
- Ví dụ: So sánh điểm thi của học sinh từ ba trường khác nhau để xem liệu có sự khác biệt về kết quả học tập hay không.
ANOVA Hai Chiều
- Biến độc lập: Hai biến phân loại.
- Biến phụ thuộc: Một biến liên tục.
- Mục đích: Phân tích không chỉ tác động riêng biệt của mỗi yếu tố mà còn xét sự tương tác giữa chúng.
- Ví dụ: Phân tích hiệu quả của chiến lược marketing trên hai yếu tố: loại sản phẩm và thời gian.
| Tiêu chí | ANOVA Một Chiều | ANOVA Hai Chiều |
|---|---|---|
| Biến độc lập | Một biến phân loại | Hai biến phân loại |
| Biến phụ thuộc | Một biến liên tục | Một biến liên tục |
| Mục đích | So sánh sự khác biệt giữa ba nhóm hoặc nhiều nhóm | So sánh sự khác biệt giữa các nhóm và tương tác giữa các yếu tố |
| Ví dụ | So sánh điểm thi giữa ba lớp học | Phân tích hiệu quả của phương pháp giảng dạy và loại lớp học |
| Kiểm tra tương tác | Không kiểm tra tương tác | Kiểm tra sự tương tác giữa hai yếu tố độc lập |
| Ứng dụng | Phân tích sự khác biệt giữa các nhóm về một yếu tố | Phân tích sự kết hợp của hai yếu tố ảnh hưởng đến kết quả nghiên cứu |
| Sử dụng phổ biến | Nghiên cứu về các nhóm độc lập | Nghiên cứu về sự kết hợp của hai yếu tố tác động |
Ví Dụ Về ANOVA
Để làm rõ hơn về ANOVA một chiều và ANOVA hai chiều, hãy cùng xem các ví dụ thực tế dưới đây:
ANOVA Một Chiều
Giả sử bạn muốn so sánh hiệu suất của ba chiến lược đầu tư khác nhau:
- Chiến lược A: Đầu tư vào cổ phiếu công nghệ (rủi ro cao, lợi nhuận cao).
- Chiến lược B: Đầu tư vào danh mục cổ phiếu và trái phiếu (rủi ro vừa phải, lợi nhuận vừa phải).
- Chiến lược C: Đầu tư vào trái phiếu và các công cụ tiền tệ (rủi ro thấp, lợi nhuận thấp).
Một ANOVA một chiều sẽ giúp bạn so sánh lợi nhuận giữa ba chiến lược này để xác định chiến lược nào mang lại hiệu quả tốt nhất.
ANOVA Hai Chiều
Giả sử bạn muốn phân tích hiệu quả của chiến lược đầu tư và điều kiện thị trường (thị trường tăng trưởng và thị trường suy thoái) đối với lợi nhuận:
ANOVA hai chiều sẽ không chỉ giúp bạn phân tích tác động riêng lẻ của mỗi yếu tố mà còn giúp xác định liệu có sự tương tác giữa chiến lược đầu tư và điều kiện thị trường hay không.
ANOVA So Với T-Test

Mặc dù cả ANOVA và t-test đều so sánh các trung bình nhóm, nhưng ANOVA có thể so sánh ba nhóm trở lên, trong khi t-test chỉ giới hạn so sánh hai nhóm. ANOVA có khả năng xử lý nhiều yếu tố đồng thời, giúp giảm nguy cơ mắc lỗi Type I.
| Tiêu chí | ANOVA | T-Test |
|---|---|---|
| Số nhóm cần so sánh | So sánh ba nhóm trở lên | So sánh hai nhóm |
| Biến độc lập | Một hoặc hai biến độc lập | Một biến độc lập |
| Mục đích | So sánh sự khác biệt giữa nhiều nhóm | So sánh sự khác biệt giữa hai nhóm |
| Ứng dụng | Phân tích khi có ba nhóm hoặc nhiều nhóm cần so sánh | Phân tích khi chỉ có hai nhóm cần so sánh |
| Kết quả | Tính toán giá trị F và các phần phân tách phương sai | Tính toán giá trị t để kiểm tra sự khác biệt |
| Lợi ích | Giảm nguy cơ lỗi Type I khi so sánh nhiều nhóm | Phù hợp cho việc so sánh giữa hai nhóm |
ANOVA Có Phụ Thuộc Vào Những Giả Thuyết Nào?
ANOVA yêu cầu ba giả thuyết chính:
- Phân phối chuẩn: Dữ liệu trong mỗi nhóm phải tuân theo phân phối chuẩn.
- Đồng nhất phương sai: Phương sai trong mỗi nhóm phải tương đương.
- Tính độc lập: Các quan sát trong mỗi nhóm phải độc lập.
Nếu các giả thuyết này bị vi phạm, kết quả của ANOVA có thể không chính xác. Trong trường hợp này, các phương pháp thay thế hoặc biến đổi dữ liệu có thể được sử dụng.
Kết Luận
ANOVA là một công cụ thống kê mạnh mẽ cho phép các nhà nghiên cứu phân tích sự khác biệt giữa ba nhóm trở lên, giúp hiểu rõ hơn về mối quan hệ giữa các yếu tố và biến phụ thuộc. Bằng cách phân tích phương sai và so sánh các nhóm, ANOVA giúp xác định những sự khác biệt có ý nghĩa và hỗ trợ ra quyết định dựa trên dữ liệu khách quan.
Cho dù bạn đang sử dụng ANOVA một chiều hay ANOVA hai chiều, phương pháp này cung cấp những hiểu biết sâu sắc về các yếu tố ảnh hưởng và tương tác trong các nghiên cứu phức tạp. Hy vọng bài viết này giúp bạn hiểu rõ hơn về ANOVA và cách áp dụng hiệu quả trong các nghiên cứu của mình, từ đó nâng cao tính chính xác và độ tin cậy của kết quả phân tích.















