Hồi quy tuyến tính bội là gì?

Hồi quy tuyến tính bội (Multiple Linear Regression – MLR) là mô hình thống kê được sử dụng để mô tả mối quan hệ giữa một biến phụ thuộc và nhiều biến độc lập thông qua một phương trình tuyến tính. Mô hình này giúp xác định mức độ ảnh hưởng của các yếu tố độc lập đến biến phụ thuộc và có thể dự báo giá trị của biến phụ thuộc dựa trên các giá trị của các biến độc lập.

Phương trình hồi quy tuyến tính bội có dạng:

Y = β₀ + β₁X₁ + β₂X₂ + ... + βnXn + ε

Trong đó:

• Y: Biến phụ thuộc (biến cần dự đoán).
• X₁, X₂, …, Xn: Các biến độc lập.
• β₀: Hằng số hồi quy (intercept).
• β₁, β₂, …, βn: Các hệ số hồi quy (slope).
• ε: Phần dư (residuals).

Các bước thực hiện phân tích hồi quy tuyến tính bội trong SPSS

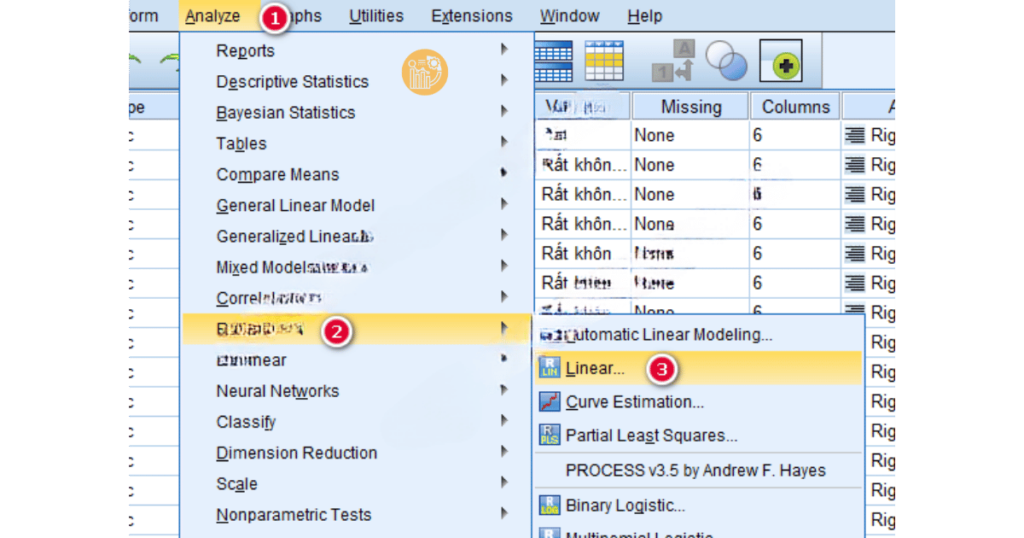
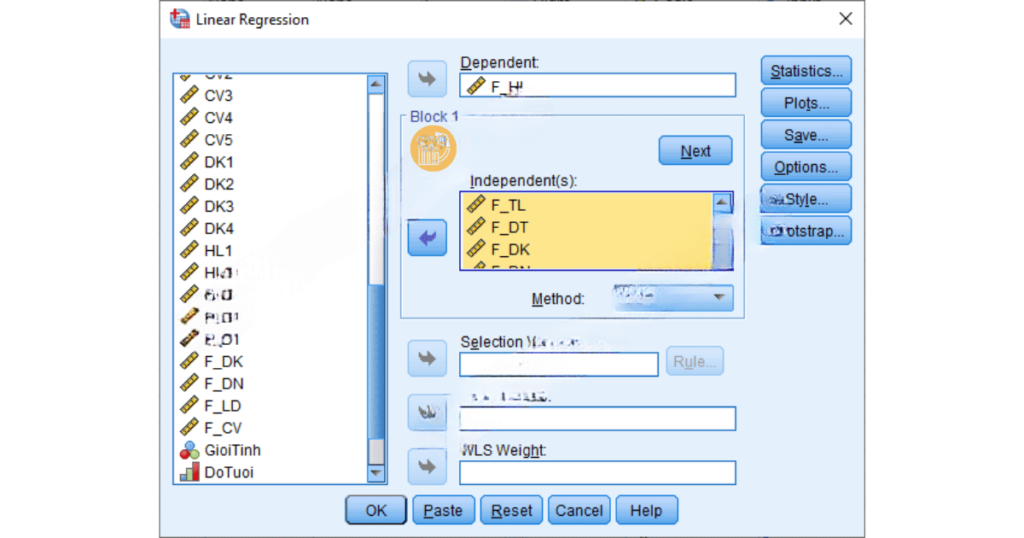
B1: Chọn phương pháp hồi quy trong SPSS: Để bắt đầu phân tích hồi quy tuyến tính bội trong SPSS, bạn vào menu Analyze > Regression > Linear. Sau đó, nhập biến phụ thuộc vào ô “Dependent” và các biến độc lập vào ô “Independent(s)”.

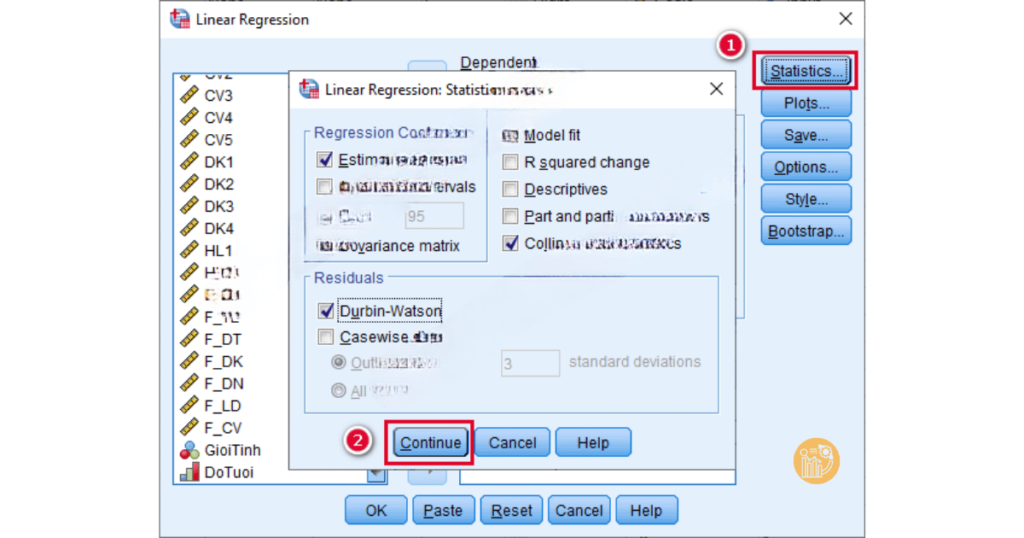
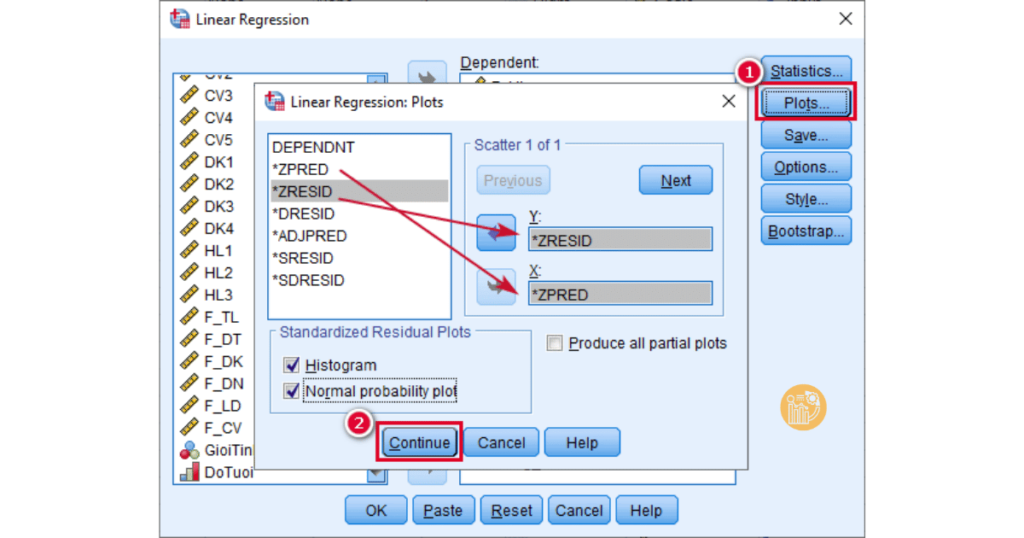
B2: Tùy chỉnh các thống kê và kiểm tra: Trong cửa sổ Linear Regression, bạn có thể chọn thêm các tùy chọn thống kê để xem các thông số như R², kiểm định t, và phân tích ANOVA. Chọn Plots để vẽ các biểu đồ, giúp kiểm tra giả thuyết về phân phối phần dư và quan hệ tuyến tính.

B3: Phương pháp nhập biến: Trong mục Method, bạn có thể chọn phương pháp đưa các biến vào mô hình. Thường dùng phương pháp Enter nếu bạn muốn đưa tất cả các biến độc lập vào một lúc. Nếu cần, bạn có thể sử dụng phương pháp Stepwise để SPSS tự động chọn các biến quan trọng nhất.

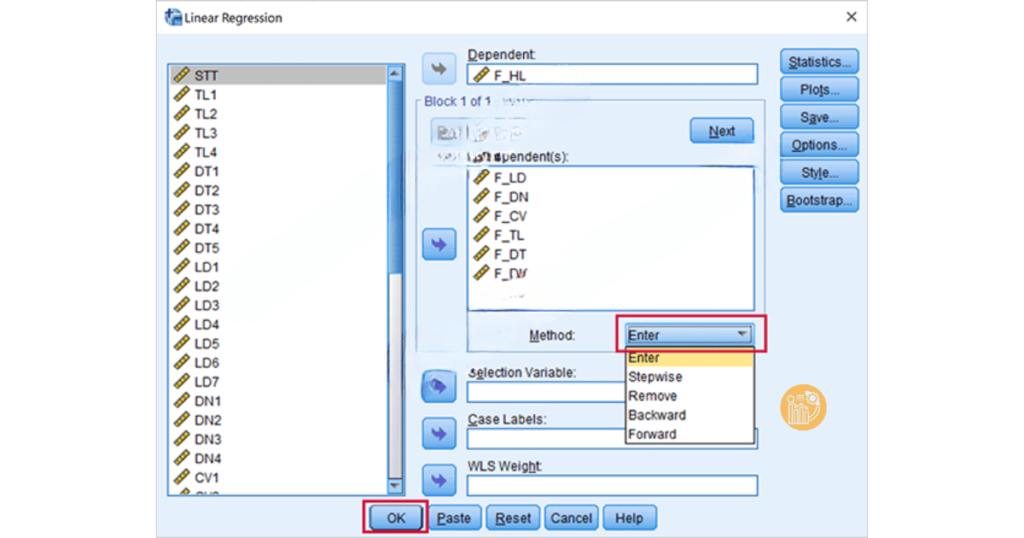
B4: Chạy phân tích và xem kết quả: Sau khi chọn xong các tùy chọn, nhấn OK để SPSS chạy phân tích và xuất ra các bảng kết quả.

Đọc kết quả phân tích hồi quy tuyến tính bội trong SPSS

Bảng ANOVA

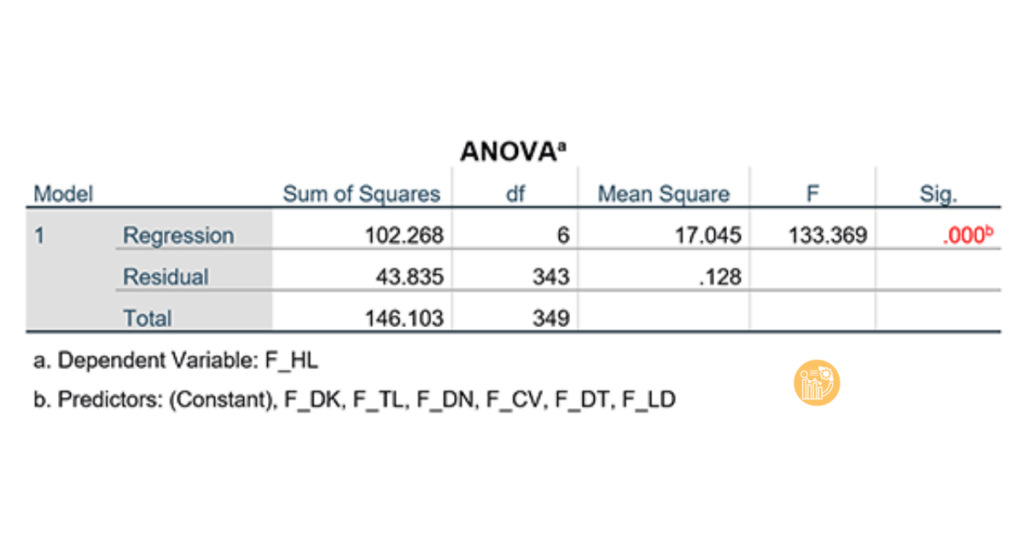
Bảng ANOVA kiểm tra độ phù hợp của mô hình hồi quy. Kiểm định F sẽ được sử dụng để kiểm tra giả thuyết rằng mô hình hồi quy không giải thích được sự biến thiên của biến phụ thuộc.

• Giá trị Sig < 0.05: Mô hình hồi quy phù hợp và có ý nghĩa thống kê.
• Giá trị Sig > 0.05: Mô hình hồi quy không có ý nghĩa thống kê.

Bảng Model Summary

Bảng này cung cấp thông tin về mức độ phù hợp của mô hình. R² là chỉ số quan trọng để đo lường mức độ biến thiên của biến phụ thuộc được giải thích bởi các biến độc lập. Adjusted R² phản ánh mức độ phù hợp của mô hình, có điều chỉnh cho số lượng biến độc lập.

• R² gần 1: Mô hình có mức độ phù hợp cao.
• Adjusted R²: Phản ánh độ chính xác của mô hình khi có nhiều biến độc lập.

Bảng Coefficients

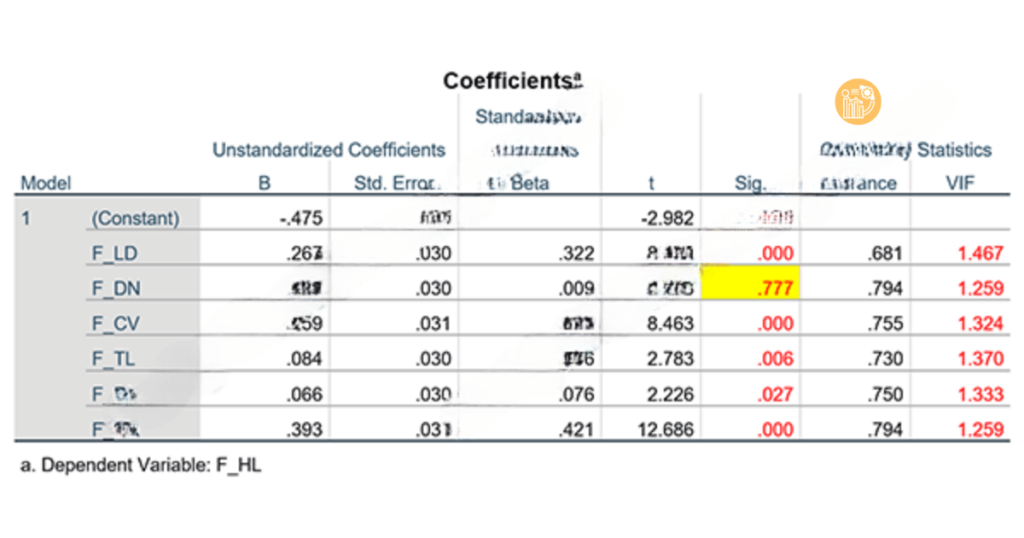
Bảng này là nơi kiểm tra ý nghĩa của các hệ số hồi quy. Bạn cần chú ý đến giá trị SIG của từng biến độc lập:

• SIG < 0.05: Hệ số hồi quy của biến có ý nghĩa thống kê và tác động lên biến phụ thuộc.
• SIG > 0.05: Hệ số hồi quy của biến không có ý nghĩa thống kê và không tác động lên biến phụ thuộc.

Kiểm định và kiểm tra giả thuyết trong hồi quy tuyến tính bội

Khi thực hiện phân tích hồi quy tuyến tính bội, chúng ta cần kiểm định các giả thuyết về mối quan hệ giữa biến phụ thuộc và các biến độc lập. Các kiểm định chính bao gồm:

• Kiểm định F: Đánh giá độ phù hợp của mô hình hồi quy.
• Kiểm định t (t-test): Kiểm tra ý nghĩa của mỗi biến độc lập trong mô hình hồi quy.
• VIF: Kiểm tra vấn đề đa cộng tuyến trong mô hình.

Ví dụ hồi quy tuyến tính bội

Giả sử bạn muốn nghiên cứu sự ảnh hưởng của các yếu tố như tiền lương, đào tạo và thăng tiến, lãnh đạo, và điều kiện làm việc đến sự hài lòng của nhân viên. Mô hình hồi quy tuyến tính bội sẽ giúp bạn xác định mức độ ảnh hưởng của từng yếu tố này.

Phương trình hồi quy có thể có dạng:

Y = 0.322 * F_LD + 0.288 * F_CV + 0.096 * F_TL + 0.076 * F_DT + 0.421 * F_DK + ε

Trong đó:

• Y là sự hài lòng của nhân viên, các biến F_LD, F_CV, F_TL, F_DT, và F_DK là các yếu tố độc lập như lãnh đạo, đồng nghiệp, thăng tiến, đào tạo và điều kiện làm việc.

Kết luận

Phân tích hồi quy tuyến tính bội trong SPSS là một công cụ mạnh mẽ giúp phân tích và dự báo mối quan hệ giữa một biến phụ thuộc và nhiều biến độc lập. Bằng cách hiểu cách đọc các bảng kết quả và kiểm định các giả thuyết, bạn có thể đánh giá chính xác mức độ tác động của các yếu tố đến biến phụ thuộc.

Nếu bạn gặp khó khăn trong việc phân tích dữ liệu hoặc muốn tham khảo thêm các bài viết và hướng dẫn chi tiết về hồi quy tuyến tính bội, hãy truy cập xulysolieu.info hoặc Xử lý số liệu để tìm hiểu thêm và nhận sự trợ giúp từ chuyên gia.