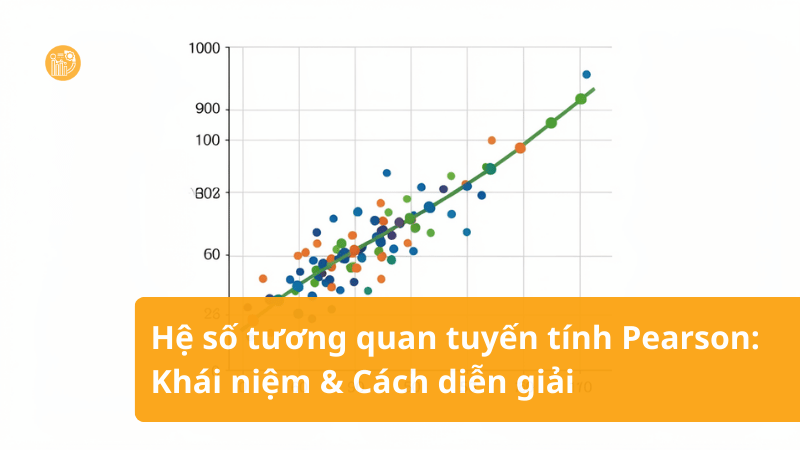
Trong phân tích dữ liệu định lượng, có một câu hỏi gần như ai cũng gặp khi bắt đầu làm thống kê: hệ số tương quan tuyến tính là gì và vì sao nó xuất hiện trong hầu hết các báo cáo nghiên cứu? Khi bạn muốn đo lường mối quan hệ giữa hai biến số (ví dụ: thu nhập và chi tiêu, thời gian học và điểm số, chất lượng dịch vụ và sự hài lòng), cách đo cơ bản nhất thường là tương quan Pearson. Tuy nhiên, nếu chỉ nhìn một con số rồi kết luận “có liên hệ” hoặc “không liên hệ” thì rất dễ sai, vì hệ số này có nhiều tính chất và hạn chế quan trọng.
Bài viết dưới đây giải thích hệ số tương quan tuyến tính là gì theo cách dễ hiểu, đi thẳng vào bản chất, kèm tính chất, giới hạn và các ví dụ kinh điển để bạn diễn giải đúng trong nghiên cứu và trong phân tích tuyến tính.
Mục lục
ToggleHệ số tương quan tuyến tính là gì?
Hệ số tương quan tuyến tính là gì? Đây là một thước đo dùng để đánh giá mức độ phụ thuộc tuyến tính giữa hai biến ngẫu nhiên (hoặc hai biến số trong dữ liệu). Hệ số tương quan tuyến tính Pearson (thường ký hiệu là r hoặc ρ) được xây dựng từ hiệp phương sai và phương sai của hai biến.
Về trực giác, tương quan Pearson trả lời câu hỏi: “Khi X tăng thì Y có xu hướng tăng theo (cùng chiều), giảm theo (ngược chiều), hay không có xu hướng tuyến tính rõ ràng?”. Vì vậy, hệ số tương quan tuyến tính là gì không chỉ là một công thức, mà là một cách đo lường mối quan hệ theo góc nhìn tuyến tính.
Giá trị của hệ số tương quan tuyến tính Pearson nằm trong khoảng từ -1 đến 1:
- Gần 1: quan hệ tuyến tính dương mạnh (X tăng thì Y thường tăng).
- Gần -1: quan hệ tuyến tính âm mạnh (X tăng thì Y thường giảm).
- Gần 0: không có quan hệ tuyến tính rõ ràng (nhưng chưa chắc “không liên hệ”).
Đến đây, bạn đã có nền tảng để trả lời hệ số tương quan tuyến tính là gì ở mức khái niệm. Phần tiếp theo sẽ giúp bạn hiểu sâu hơn về tính chất và cách diễn giải.
Tính chất quan trọng của tương quan Pearson
Để diễn giải đúng, bạn cần nắm một vài tính chất cốt lõi. Tính chất đầu tiên: hệ số tương quan tuyến tính là gì về mặt ý nghĩa? Nó là thước đo sự phụ thuộc tuyến tính. Nếu hai biến có quan hệ tuyến tính “hoàn hảo”, nghĩa là Y bằng aX + b gần như mọi nơi (với a khác 0), thì tương quan Pearson sẽ có trị tuyệt đối bằng 1. Đây là dấu hiệu mạnh nhất của quan hệ tuyến tính.
Tính chất thứ hai: tương quan Pearson không đổi qua phép biến đổi tuyến tính với hệ số dương. Nói dễ hiểu, nếu bạn đổi đơn vị đo (ví dụ đổi từ “triệu” sang “nghìn”, hoặc chuẩn hóa dữ liệu), thì hệ số tương quan tuyến tính là gì vẫn giữ nguyên về bản chất. Điều này rất hữu ích trong phân tích dữ liệu định lượng vì nó giúp bạn so sánh mối quan hệ mà không bị ảnh hưởng bởi thang đo.
Tuy nhiên, nếu phép biến đổi tuyến tính có hệ số âm (ví dụ nhân -1), dấu của hệ số tương quan sẽ đổi chiều. Đây là điểm nhỏ nhưng rất hay gặp khi bạn đảo mã thang đo.
Hệ số tương quan tuyến tính đo được gì và không đo được gì?
Phần này là nơi nhiều người hiểu sai. Hệ số tương quan tuyến tính là gì? Nó đo mức độ liên hệ tuyến tính, không phải mọi dạng liên hệ. Có những trường hợp X và Y liên quan rất mạnh nhưng theo dạng phi tuyến, khi đó tương quan Pearson có thể gần 0 và khiến bạn tưởng “không có mối quan hệ”.
Dưới đây là các hạn chế quan trọng cần nhớ khi dùng tương quan Pearson trong thống kê mô tả và phân tích tuyến tính:
- Chỉ đo phụ thuộc tuyến tính: nếu quan hệ là đường cong, r có thể thấp.
- Không bảo toàn qua biến đổi phi tuyến: lấy bình phương, log, mũ… có thể làm r thay đổi mạnh.
- Chỉ cho biết “mức độ” chứ không mô tả rõ “cấu trúc” phụ thuộc (dạng quan hệ cụ thể).
- Không xác định hoàn toàn phân phối chung của hai biến: cùng r nhưng dữ liệu có thể khác rất xa.
- Với Y là hàm phi tuyến của X, tương quan Pearson thường nhỏ hơn 1 dù dự đoán có thể rất tốt.
Vì vậy, khi trả lời hệ số tương quan tuyến tính là gì trong thực hành, bạn nên kèm thêm câu: “Nó chỉ phản ánh phần tuyến tính của mối quan hệ”.
Cách diễn giải hệ số tương quan tuyến tính trong phân tích dữ liệu
Trong phân tích dữ liệu định lượng, bạn thường diễn giải theo hai lớp: chiều hướng (dương/âm) và mức độ (mạnh/yếu). Một cách diễn giải đơn giản:
- 0.00–0.19: rất yếu
- 0.20–0.39: yếu
- 0.40–0.59: trung bình
- 0.60–0.79: mạnh
- 0.80–1.00: rất mạnh
Các ngưỡng này chỉ mang tính tham khảo và phụ thuộc lĩnh vực. Trong khoa học xã hội, r khoảng 0.30 đôi khi đã có ý nghĩa thực tiễn, còn trong kỹ thuật có thể cần cao hơn. Quan trọng hơn, hệ số tương quan tuyến tính là gì cũng phải đi kèm kiểm định ý nghĩa thống kê (p-value) nếu bạn muốn kết luận trên tổng thể.
Một lưu ý: tương quan không đồng nghĩa nhân quả. Hai biến có thể tương quan cao vì cùng bị ảnh hưởng bởi biến thứ ba. Vì vậy, trong báo cáo, bạn nên dùng ngôn ngữ “liên hệ” hoặc “đồng biến/ nghịch biến” thay vì “gây ra”.
Ba ví dụ giúp hiểu đúng “r = 0”
Đây là phần quan trọng nhất để tránh ngộ nhận. Rất nhiều người thấy r = 0 rồi kết luận “hai biến độc lập”. Thực tế, r = 0 chỉ nói rằng không có liên hệ tuyến tính, còn liên hệ phi tuyến vẫn có thể tồn tại.
Ví dụ 1: Quan hệ phi tuyến đối xứng
Giả sử Y = X2 và X đối xứng quanh 0. Khi đó, giá trị dương và âm của X tạo ra Y giống nhau, dẫn đến tương quan Pearson có thể bằng 0. Nhưng rõ ràng nếu biết X, bạn dự đoán được Y rất tốt. Trường hợp này cho thấy hệ số tương quan tuyến tính là gì: nó “không thấy” mối quan hệ dạng đường cong đối xứng.
Ví dụ 2: Tương quan bằng 0 nhưng vẫn phụ thuộc
Có những phân phối hai chiều mà tương quan Pearson bằng 0, nhưng X và Y không độc lập. Điều này thường xảy ra khi cấu trúc phụ thuộc bị “triệt tiêu” theo kiểu đối xứng, khiến hiệp phương sai bằng 0. Đây là lý do bạn không nên dùng r = 0 để khẳng định độc lập, nhất là trong nghiên cứu định lượng có dữ liệu phức tạp.
Ví dụ 3: Không tương quan nhưng dự đoán “gần như hoàn hảo”
Một số cấu trúc dữ liệu có thể cho r = 0 nhưng vẫn dự đoán tốt nếu biết biến còn lại, vì quan hệ nằm ở dạng phi tuyến hoặc ràng buộc theo miền giá trị. Ví dụ này nhắc lại rằng hệ số tương quan tuyến tính là gì: nó không mô tả đầy đủ cấu trúc phụ thuộc, chỉ đo phần tuyến tính.
Khi nào nên dùng tương quan Pearson trong thống kê mô tả?
Trong thống kê mô tả, tương quan Pearson phù hợp khi:
- Bạn muốn đo lường mối quan hệ giữa hai biến định lượng.
- Bạn nghi ngờ quan hệ gần tuyến tính (hoặc muốn kiểm tra giả thuyết tuyến tính).
- Dữ liệu không bị ngoại lệ (outlier) quá mạnh làm méo r.
Nếu bạn nghi ngờ quan hệ phi tuyến, hãy xem thêm scatter plot, hoặc cân nhắc tương quan Spearman (xếp hạng) như một lựa chọn bổ sung trong phân tích dữ liệu định lượng.
Kết luận
Hệ số tương quan tuyến tính là gì? Đó là thước đo mức độ phụ thuộc tuyến tính giữa hai biến, thường được thực hiện bằng tương quan Pearson trong thống kê mô tả và phân tích tuyến tính. Tuy nhiên, r chỉ phản ánh mối quan hệ theo đường thẳng; r gần 0 không có nghĩa là hai biến độc lập, và r cao cũng không chứng minh quan hệ nhân quả. Muốn diễn giải đúng, bạn nên kết hợp r với biểu đồ phân tán và bối cảnh nghiên cứu.
Nếu bạn cần hỗ trợ tính tương quan pearson, kiểm tra giả định, trực quan hóa mối quan hệ hoặc phân tích dữ liệu định lượng cho nghiên cứu, hãy liên hệ với xulysolieu.info – Xử lý số liệu hoặc truy cập xulysolieu.info. Hotline: 0878968468.