Khám Phá Tin Học Ứng Dụng SPSS
Tin học ứng dụng SPSS là một công cụ mạnh mẽ hỗ trợ trong việc phân tích dữ liệu, giúp người dùng đưa ra quyết định thông minh dựa vào các kết quả số liệu. Với sức mạnh và tính linh hoạt của nó, SPSS đã trở thành một phần quan trọng trong nhiều lĩnh vực như nghiên cứu thị trường, khoa học xã hội, giáo dục, và y tế.
Lịch Sử và Phát Triển SPSS
SPSS (Statistical Package for the Social Sciences) ra đời vào năm 1968, được phát triển bởi Norman H. Nie, C. Hadlai Hull, và William G. M. Steinbrenner. Ban đầu, phần mềm này được thiết kế cho các nhà nghiên cứu xã hội nhằm đơn giản hóa quá trình phân tích thống kê mà không cần phải có kiến thức sâu về lập trình máy tính.
Những Ngày Đầu Tiên Của SPSS
Trong những năm đầu, SPSS chỉ bao gồm một số tính năng cơ bản như phân tích tần suất, phân bố xác suất và hồi quy tuyến tính. Tuy nhiên, nhờ vào tính dễ sử dụng và khả năng xử lý dữ liệu mạnh mẽ, SPSS nhanh chóng chiếm lĩnh thị trường.
Sự Phát Triển Và Cải Tiến
Theo thời gian, SPSS đã trải qua nhiều giai đoạn phát triển. Năm 2009, IBM đã mua lại SPSS, dẫn đến việc cập nhật và bổ sung rất nhiều tính năng mới. Hiện tại, SPSS không chỉ phục vụ cho các nhà nghiên cứu xã hội mà còn mở rộng sang các lĩnh vực khác như y tế, tài chính, và marketing.
Một Số Phiên Bản Nổi Bật
- SPSS Base: Bao gồm các công cụ phân tích cơ bản.
- SPSS Advanced Statistics: Cung cấp thêm các phương pháp phân tích nâng cao như ANOVA và hồi quy logistic.
- SPSS Regression: Tập trung vào các phương pháp hồi quy.
- SPSS Custom Tables: Giúp tạo báo cáo và bảng tùy chỉnh theo nhu cầu người dùng.
Chức Năng Chính Của SPSS

SPSS cung cấp nhiều chức năng hữu ích cho việc phân tích dữ liệu. Dưới đây là một cái nhìn tổng quát về những chức năng chính mà SPSS mang lại.
Phân Tích Thống Kê
Phân tích thống kê là một trong những chức năng cơ bản của SPSS. Người dùng có thể thực hiện các phép thử thống kê như:
- Phân tích tần suất
- Kiểm định giả thuyết
- Phân tích phương sai
Mỗi loại phân tích đều có mục đích riêng, từ việc kiểm tra sự phân bố của dữ liệu đến việc đánh giá mối quan hệ giữa các biến số.
Xử Lý Dữ Liệu
SPSS cung cấp các công cụ để làm sạch và chuẩn bị dữ liệu trước khi tiến hành phân tích. Những công cụ này bao gồm:
- Xử lý dữ liệu thiếu
- Chuyển đổi biến
- Tính toán các chỉ tiêu thống kê mô tả
Việc xử lý dữ liệu đúng cách sẽ đảm bảo độ tin cậy và chính xác của các kết quả phân tích.
Tạo Biểu Đồ Và Báo Cáo
Một trong những điểm mạnh của SPSS là khả năng tạo biểu đồ và báo cáo dễ hiểu. Người dùng có thể tạo ra:
- Biểu đồ cột
- Biểu đồ đường
- Biểu đồ phân tán
Các biểu đồ này không chỉ giúp người dùng hình dung dữ liệu một cách trực quan mà còn hỗ trợ trong việc trình bày kết quả phân tích.
Ứng Dụng Của SPSS Trong Các Lĩnh Vực
SPSS được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Mỗi lĩnh vực có cách sử dụng SPSS riêng biệt nhằm đáp ứng các nhu cầu đặc thù.
Trong Nghiên Cứu Khoa Học Xã Hội
Các nhà nghiên cứu trong lĩnh vực khoa học xã hội thường sử dụng SPSS để phân tích các dữ liệu khảo sát. Những ứng dụng phổ biến bao gồm:
- Phân tích mối quan hệ giữa các yếu tố xã hội
- Đánh giá hiệu quả của các chương trình can thiệp
- Nghiên cứu hành vi người tiêu dùng
Với SPSS, các nhà nghiên cứu có thể thu thập và phân tích dữ liệu một cách nhanh chóng và chính xác.
Trong Giáo Dục
SPSS đóng vai trò quan trọng trong giáo dục, giúp giảng viên và sinh viên phân tích dữ liệu nghiên cứu và bài tập. Những ứng dụng bao gồm:
- Phân tích kết quả kiểm tra
- Xem xét sự khác biệt giữa các nhóm học sinh
- Nghiên cứu xu hướng học tập
Điều này không chỉ giúp cải thiện chất lượng giảng dạy mà còn nâng cao khả năng phân tích của sinh viên.
Trong Y Tế
Trong lĩnh vực y tế, SPSS được sử dụng để phân tích dữ liệu lâm sàng và nghiên cứu epidemiology. Một số ứng dụng đáng chú ý là:
- Phân tích hiệu quả điều trị
- Nghiên cứu sự lây lan của bệnh dịch
- Đánh giá chất lượng dịch vụ y tế
Nhờ vào SPSS, các chuyên gia y tế có thể đưa ra những quyết định sáng suốt hơn trong việc chăm sóc sức khỏe cộng đồng.
Các Bước Để Làm Chủ SPSS

Để sử dụng SPSS hiệu quả, người dùng cần nắm vững một số bước cơ bản trong quy trình làm việc.
Bắt Đầu Với SPSS
Trước tiên, người dùng cần cài đặt phần mềm SPSS trên máy tính. Sau khi cài đặt xong, người dùng có thể bắt đầu tạo một dự án mới và nhập dữ liệu vào SPSS.
Nhập Dữ Liệu
Dữ liệu có thể được nhập trực tiếp vào SPSS hoặc thông qua các nguồn dữ liệu khác như Excel hay CSV. Việc nhập dữ liệu đúng cách là cực kỳ quan trọng để đảm bảo tính chính xác trong quá trình phân tích.
Phân Tích Dữ Liệu
Sau khi dữ liệu đã được nhập, người dùng có thể tiến hành phân tích bằng cách lựa chọn các phương pháp thống kê phù hợp với mục tiêu nghiên cứu. Điều này bao gồm việc chạy các phép thử thống kê và tạo báo cáo.
Trình Bày Kết Quả
Cuối cùng, kết quả phân tích nên được trình bày một cách rõ ràng và dễ hiểu. Người dùng có thể tạo báo cáo, biểu đồ và đưa ra các nhận định dựa trên kết quả phân tích.
Kết luận
Tin học ứng dụng SPSS đã chứng tỏ được vị trí quan trọng của mình trong việc phân tích dữ liệu, phục vụ cho nhiều lĩnh vực khác nhau từ khoa học xã hội đến y tế. Với những chức năng phong phú và khả năng xử lý mạnh mẽ, SPSS giúp người dùng đưa ra những quyết định sáng suốt dựa trên dữ liệu. Học hỏi và làm chủ SPSS không chỉ là một lợi thế trong công việc mà còn mở ra nhiều cơ hội nghề nghiệp hấp dẫn trong tương lai.
Cách chạy spss câu hỏi nhiều lựa chọn – Hướng dẫn chi tiết
Cách chạy spss câu hỏi nhiều lựa chọn là một trong những bước quan trọng khi bạn muốn phân tích dữ liệu từ các khảo sát hoặc nghiên cứu xã hội. Phần mềm SPSS (Statistical Package for the Social Sciences) được sử dụng rộng rãi bởi các nhà nghiên cứu và chuyên gia thống kê để xử lý và phân tích dữ liệu một cách hiệu quả. Trong bài viết này, chúng ta sẽ cùng tìm hiểu quy trình và kỹ thuật cần thiết để thực hiện phân tích câu hỏi nhiều lựa chọn trong SPSS.
Hiểu rõ về câu hỏi nhiều lựa chọn trong nghiên cứu
Trước khi đi vào cách chạy SPSS câu hỏi nhiều lựa chọn, chúng ta cần hiểu rõ về bản chất của câu hỏi này và tầm quan trọng của nó trong nghiên cứu.
Định nghĩa câu hỏi nhiều lựa chọn
Câu hỏi nhiều lựa chọn thường được sử dụng trong các cuộc khảo sát nhằm thu thập ý kiến, đánh giá hoặc thông tin từ người tham gia. Người tham gia sẽ có thể chọn một hoặc nhiều lựa chọn từ một danh sách được cung cấp. Ví dụ: “Bạn thích loại hình giải trí nào nhất?” với các lựa chọn như phim ảnh, âm nhạc, thể thao, sách…
Tại sao nên sử dụng câu hỏi nhiều lựa chọn?
Việc sử dụng câu hỏi nhiều lựa chọn mang lại nhiều lợi ích, bao gồm:
- Dễ dàng phân tích: Dữ liệu từ câu hỏi nhiều lựa chọn dễ dàng được mã hóa và phân tích bằng các công cụ thống kê.
- Thúc đẩy sự phản hồi: Người tham gia có động lực hơn khi họ không cần phải viết câu trả lời mở mà chỉ cần chọn một lựa chọn.
- Tiết kiệm thời gian: Câu hỏi nhiều lựa chọn giúp người tham gia hoàn thành khảo sát nhanh chóng, từ đó tăng tỷ lệ phản hồi.
Các yếu tố cần xem xét khi xây dựng câu hỏi nhiều lựa chọn
Khi thiết kế câu hỏi nhiều lựa chọn, bạn cần chú ý đến những yếu tố sau:
- Sự rõ ràng của lựa chọn: Mỗi lựa chọn phải rõ ràng và không gây nhầm lẫn cho người tham gia.
- Số lượng lựa chọn: Nên giới hạn số lượng lựa chọn để không làm khó chịu người tham gia, nhưng cũng đủ để phủ kín các khả năng.
- Tính đa dạng: Đảm bảo rằng các lựa chọn phản ánh đúng sự đa dạng trong quần thể mục tiêu của bạn.
Cài đặt và chuẩn bị dữ liệu trong SPSS

Trước khi thực hiện phân tích, bạn cần chuẩn bị dữ liệu một cách chính xác trong SPSS. Điều này bao gồm việc nhập dữ liệu khảo sát và cấu hình các thuộc tính cho câu hỏi nhiều lựa chọn.
Nhập dữ liệu vào SPSS
Để bắt đầu, bạn cần nhập dữ liệu khảo sát vào SPSS. Dưới đây là các bước cơ bản:
- Mở phần mềm SPSS và tạo một file mới.
- Chuyển sang chế độ “Data View” để nhập dữ liệu. Mỗi cột sẽ đại diện cho một biến tương ứng với từng câu hỏi trong khảo sát.
- Nhập dữ liệu từ bảng khảo sát vào các ô tương ứng. Đối với câu hỏi nhiều lựa chọn, bạn có thể mã hóa các lựa chọn bằng các số hoặc ký tự.
Cấu hình các thuộc tính cho biến
Sau khi nhập dữ liệu, bạn cần cấu hình các thuộc tính cho biến để SPSS hiểu đúng về chúng. Thực hiện theo các bước sau:
- Chuyển sang chế độ “Variable View”.
- Thiết lập tên biến và loại dữ liệu (numeric cho các câu hỏi nhiều lựa chọn).
- Bạn có thể định nghĩa các giá trị cho các lựa chọn của câu hỏi nhiều lựa chọn trong ô “Values”. Ví dụ, nếu bạn có 4 lựa chọn, bạn có thể quy định 1 là “Phim”, 2 là “Âm nhạc”, 3 là “Thể thao”, 4 là “Sách”.
Kiểm tra và sửa lỗi dữ liệu
Sau khi nhập xong, việc kiểm tra lại dữ liệu là rất quan trọng. Hãy xem lại từng ô để đảm bảo không có lỗi chính tả hay nhập sai giá trị. Sử dụng chức năng “Descriptive Statistics” trong SPSS để phát hiện các giá trị ngoại lai hoặc lỗi dữ liệu.
Phân tích dữ liệu câu hỏi nhiều lựa chọn trong SPSS
Khi đã hoàn tất việc nhập và cấu hình dữ liệu, bạn có thể tiến hành phân tích dữ liệu câu hỏi nhiều lựa chọn với SPSS. Các phương pháp phân tích phổ biến bao gồm tần suất, biểu đồ và phân tích tương quan.
Thực hiện phân tích tần suất
Phân tích tần suất giúp bạn biết được số lượng người tham gia chọn mỗi lựa chọn trong câu hỏi nhiều lựa chọn. Để thực hiện phân tích này, bạn làm theo các bước:
- Vào menu “Analyze” -> “Descriptive Statistics” -> “Frequencies”.
- Chọn các biến cần phân tích và đưa vào ô “Variables”.
- Nhấn “OK” và SPSS sẽ hiển thị bảng tần suất cho bạn.
Khi bạn nhìn vào bảng tần suất, bạn sẽ thấy số lượng người tham gia đã chọn mỗi lựa chọn. Điều này giúp bạn hiểu được xu hướng và sở thích của nhóm đối tượng khảo sát.
Tạo biểu đồ trực quan
Để dễ dàng truyền tải thông tin, việc tạo biểu đồ từ kết quả phân tích tần suất là rất hữu ích.
- Vào menu “Graphs” -> “Chart Builder”.
- Chọn kiểu biểu đồ phù hợp (biểu đồ cột, biểu đồ tròn, v.v.) và kéo thả vào khu vực biểu đồ.
- Chọn biến bạn đã phân tích và nhấn “OK”.
Biểu đồ sẽ giúp bạn trình bày dữ liệu một cách sinh động và trực quan hơn, giúp các bên liên quan dễ dàng hiểu và tiếp cận thông tin.
Phân tích tương quan giữa các biến
Nếu câu hỏi nhiều lựa chọn nằm trong một bộ dữ liệu lớn hơn, bạn có thể muốn xem xét mối quan hệ giữa các biến khác nhau. SPSS cung cấp nhiều phương pháp để thực hiện điều này, bao gồm phân tích hồi quy và phân tích chi-square.
- Để thực hiện phân tích hồi quy, vào menu “Analyze” -> “Regression” -> “Linear”, chọn biến phụ thuộc và biến độc lập.
- Với phân tích chi-square, vào menu “Analyze” -> “Descriptive Statistics” -> “Crosstabs”, chọn các biến và nhấn “OK”.
Phân tích này không chỉ giúp bạn hiểu sâu hơn về mối quan hệ giữa các biến mà còn cung cấp cái nhìn tổng thể về dữ liệu khảo sát.
Đánh giá và diễn giải kết quả phân tích

Khi đã thực hiện các bước phân tích, bước tiếp theo là đánh giá và diễn giải kết quả một cách chính xác. Đây là bước rất quan trọng vì nó giúp bạn rút ra các kết luận và khuyến nghị dựa trên dữ liệu.
Đọc và hiểu bảng kết quả
Bảng kết quả mà SPSS cung cấp sẽ chứa nhiều thông tin quý giá. Hãy chú ý đến các thông số như giá trị p, mức độ tin cậy, và các chỉ số thống kê khác.
- Giá trị p sẽ cho bạn biết liệu có sự khác biệt có ý nghĩa thống kê giữa các nhóm không. Nếu giá trị p nhỏ hơn 0.05, bạn có thể coi là có sự khác biệt.
- Mức độ tin cậy (confidence intervals) sẽ cho bạn biết phạm vi của giá trị trung bình mà bạn có thể kỳ vọng nhận được.
Diễn giải bảng tần suất và biểu đồ
Sau khi đọc bảng tần suất và biểu đồ, hãy cố gắng diễn giải ý nghĩa của chúng trong ngữ cảnh nghiên cứu của bạn.
- Xem xét sự phân bố của các lựa chọn và tìm hiểu liệu có sự tập trung nào đó về sở thích hay ý kiến không.
- Từ biểu đồ, bạn có thể dễ dàng nhận thấy xu hướng và so sánh giữa các lựa chọn khác nhau.
Liên kết kết quả với giả thuyết nghiên cứu
Cuối cùng, hãy liên kết kết quả phân tích với giả thuyết hoặc câu hỏi nghiên cứu ban đầu của bạn.
- Nếu kết quả hỗ trợ giả thuyết, hãy nêu rõ cách mà dữ liệu chất lượng cao có thể củng cố quan điểm của bạn.
- Ngược lại, nếu kết quả không như mong đợi, hãy cân nhắc các yếu tố có thể đã ảnh hưởng đến độ tin cậy của dữ liệu.
Kết luận
Cách chạy spss câu hỏi nhiều lựa chọn có thể không phức tạp như nhiều người nghĩ. Qua các bước từ việc nhập dữ liệu, cấu hình các thuộc tính, đến phân tích tần suất và đánh giá kết quả, bạn có thể dễ dàng áp dụng SPSS để phân tích dữ liệu từ khảo sát của mình. Việc hiểu rõ quy trình và các công cụ phân tích là chìa khóa để bạn khai thác tối đa giá trị từ dữ liệu của mình. Hãy nhớ rằng, phân tích dữ liệu không chỉ dừng lại ở việc lấy số liệu, mà còn là việc rút ra những thông tin ý nghĩa và phục vụ cho mục đích nghiên cứu của bạn.
Thống Kê và Xử Lý Dữ Liệu UTC: Hướng Dẫn Chi Tiết
Thống kê và xử lý dữ liệu UTC là một lĩnh vực quan trọng trong thời đại số hóa hiện nay. Việc hiểu rõ về cách thức thống kê và xử lý dữ liệu theo định dạng ngày giờ UTC sẽ giúp chúng ta quản lý và phân tích thông tin một cách hiệu quả hơn, đồng thời tối ưu hóa các quy trình làm việc.
Tổng Quan Về Định Nghĩa UTC
Để hiểu rõ về thống kê và xử lý dữ liệu UTC, trước tiên chúng ta cần biết định nghĩa cơ bản về UTC.
Định Nghĩa UTC
UTC (Coordinated Universal Time) được xem như múi giờ chuẩn toàn cầu. Nó không thay đổi khi có chuyển mùa hay các yếu tố khác. Điều này giúp cho việc giao tiếp và trao đổi thông tin trở nên thuận lợi hơn trên toàn thế giới.
Lịch Sử Phát Triển của UTC
UTC ra đời vào năm 1960 nhằm mục đích đồng bộ hóa thời gian giữa các quốc gia. Trước đó, mỗi quốc gia hoặc khu vực sử dụng múi giờ riêng, gây khó khăn trong việc liên lạc và hợp tác quốc tế. UTC đã giúp giải quyết vấn đề này bằng cách cung cấp một tiêu chuẩn thống nhất.
Tại Sao Cần Sử Dụng UTC?
Việc sử dụng UTC giúp đảm bảo rằng mọi người đều có thể truy cập và chia sẻ thông tin mà không gặp phải sự nhầm lẫn về múi giờ. Đặc biệt là trong lĩnh vực công nghệ thông tin, nơi mà dữ liệu được truyền tải và xử lý qua nhiều múi giờ khác nhau.
Quản Lý Múi Giờ Trong Thống Kê Dữ Liệu

Khi làm việc với dữ liệu thời gian, quản lý múi giờ là rất quan trọng. Những khác biệt về múi giờ có thể ảnh hưởng đến việc phân tích và ghi nhận dữ liệu.
Các Vấn Đề Thường Gặp Khi Quản Lý Múi Giờ
Một trong những vấn đề chính khi quản lý múi giờ là sự khác biệt về thời gian giữa các khu vực. Điều này có thể dẫn đến việc mất mát hoặc sai lệch dữ liệu nếu không được xử lý đúng cách.
Ngoài ra, một số hệ thống không hỗ trợ tự động chuyển đổi giữa các múi giờ, điều này có thể gây ra sự phức tạp trong quá trình thu thập và xử lý dữ liệu.
Giải Pháp Quản Lý Múi Giờ
Để đối phó với các vấn đề này, bạn có thể áp dụng một số giải pháp quản lý múi giờ:
- Sử Dụng UTC Làm Chuẩn: Đặt UTC là thời gian chuẩn cho tất cả các hoạt động. Điều này giúp loại bỏ sự nhầm lẫn.
- Chuyển Đổi Múi Giờ Tự Động: Sử dụng phần mềm có khả năng tự động chuyển đổi giữa các múi giờ từ UTC sang thời gian địa phương và ngược lại.
- Đào Tạo Nhân Viên: Đảm bảo rằng tất cả nhân viên đều hiểu rõ về múi giờ và cách thức hoạt động của nó sẽ giúp giảm thiểu sai lầm.
Tính Toán Thời Gian Chênh Lệch
Khi làm việc với dữ liệu từ nhiều múi giờ khác nhau, việc tính toán thời gian chênh lệch là rất cần thiết. Bạn có thể sử dụng các công cụ lập trình hoặc phần mềm để dễ dàng thực hiện phép tính này.
Định Dạng Ngày Giờ UTC Trong Thống Kê Dữ Liệu

Một phần quan trọng trong việc thống kê và xử lý dữ liệu theo định dạng UTC là việc hiểu rõ về cách định dạng ngày giờ.
Quy Tắc Định Dạng Ngày Giờ
Theo tiêu chuẩn ISO 8601, định dạng ngày giờ UTC thường được viết như sau: YYYY-MM-DDTHH:mm:ssZ.
Trong đó:
- YYYY: Năm
- MM: Tháng
- DD: Ngày
- HH: Giờ
- mm: Phút
- ss: Giây
- Z: Chỉ ra rằng thời gian là UTC
Ví Dụ Cụ Thể
Ví dụ, nếu bạn muốn biểu thị thời gian là 3 giờ chiều ngày 10 tháng 12 năm 2023 theo giờ UTC, bạn sẽ viết là 2023-12-10T15:00:00Z.
Lợi Ích Của Định Dạng UTC
Sử dụng định dạng UTC có nhiều lợi ích, bao gồm:
- Giảm thiểu sự nhầm lẫn về thời gian.
- Dễ dàng so sánh dữ liệu từ nhiều nguồn khác nhau.
- Tối ưu hóa khả năng đồng bộ dữ liệu khi làm việc với nhiều múi giờ.
Phân Tích Dữ Liệu Thời Gian Thực

Phân tích dữ liệu thời gian thực là một lĩnh vực ngày càng phát triển, đặc biệt trong các hệ thống giám sát.
Khái Niệm Phân Tích Dữ Liệu Thời Gian Thực
Phân tích dữ liệu thời gian thực đề cập đến việc thu thập, xử lý và phân tích dữ liệu ngay lập tức khi chúng được tạo ra. Điều này mang lại những cái nhìn sâu sắc và kịp thời cho người sử dụng.
Ứng Dụng Phân Tích Dữ Liệu Thời Gian Thực
Trong nhiều lĩnh vực, phân tích dữ liệu thời gian thực đóng vai trò quan trọng. Một số ứng dụng bao gồm:
- Giám sát tình hình tài chính: Theo dõi biến động giá cổ phiếu trong thời gian thực.
- Quản lý giao thông: Cung cấp thông tin về tình trạng giao thông ngay lập tức.
- An ninh mạng: Phát hiện và phản ứng nhanh với các cuộc tấn công mạng.
Công Cụ Phân Tích Dữ Liệu Thời Gian Thực
Có nhiều công cụ và nền tảng hỗ trợ phân tích dữ liệu thời gian thực. Một số công cụ phổ biến bao gồm Apache Kafka, Apache Flink và Google BigQuery.
Tối Ưu Hóa Xử Lý Dữ Liệu

Cuối cùng, để đảm bảo rằng việc thống kê và xử lý dữ liệu UTC diễn ra hiệu quả, việc tối ưu hóa quy trình là rất quan trọng.
Các Kỹ Thuật Tối Ưu Hóa
Có nhiều kỹ thuật để tối ưu hóa xử lý dữ liệu, bao gồm:
- Sử Dụng Bộ Nhớ Cache: Giúp tăng tốc độ truy cập dữ liệu bằng cách lưu trữ tạm thời dữ liệu mà bạn truy cập thường xuyên.
- Chia Nhỏ Dữ Liệu: Phân chia dữ liệu thành từng phần nhỏ hơn giúp cải thiện hiệu suất xử lý.
- Sử Dụng Kiến Trúc Microservices: Tạo ra các dịch vụ độc lập giúp việc bảo trì và mở rộng trở nên dễ dàng hơn.
Lợi Ích của Tối Ưu Hóa
Tối ưu hóa không chỉ giúp cải thiện hiệu suất, mà còn giảm chi phí vận hành. Khi dữ liệu được xử lý nhanh hơn, bạn có thể đưa ra quyết định kịp thời và chính xác.
Các Xu Hướng Tương Lai
Các xu hướng mới trong xử lý dữ liệu đang nổi lên như trí tuệ nhân tạo và machine learning sẽ tiếp tục thúc đẩy việc tối ưu hóa quy trình phân tích dữ liệu.
Kết luận
Tóm lại, việc thống kê và xử lý dữ liệu UTC là một phần quan trọng trong bất kỳ tổ chức nào. Hiểu rõ về quản lý múi giờ, định dạng ngày giờ UTC, phân tích dữ liệu thời gian thực, cùng với tối ưu hóa quy trình xử lý dữ liệu sẽ giúp bạn nâng cao hiệu quả công việc của mình. Bằng việc áp dụng các chiến lược và công cụ phù hợp, bạn có thể khai thác tối đa giá trị từ dữ liệu mà bạn đang làm việc.
Cách chạy SPSS từ Excel – Hướng dẫn chi tiết
Trong bài viết này, chúng ta sẽ khám phá cách chạy SPSS từ Excel một cách dễ dàng và hiệu quả. SPSS (Statistical Package for the Social Sciences) là một phần mềm phân tích dữ liệu mạnh mẽ, thường được sử dụng trong nghiên cứu xã hội học, tâm lý học và nhiều lĩnh vực khác. Việc chuyển đổi dữ liệu từ Excel sang SPSS và nắm bắt cách chạy SPSS từ Excel có thể giúp bạn tận dụng tối đa những tính năng của cả 2 phần mềm này.
Tại sao nên sử dụng SPSS để phân tích dữ liệu?

SPSS không chỉ đơn thuần là một công cụ phân tích số liệu mà còn là một giải pháp toàn diện cho việc xử lý và trình bày dữ liệu. Khi bạn hiểu rõ về cách chạy SPSS từ Excel, bạn sẽ thấy rằng việc phân tích dữ liệu trở nên dễ dàng hơn rất nhiều.
Đặc điểm nổi bật của SPSS
SPSS có nhiều tính năng mạnh mẽ như phân tích hồi quy, kiểm định giả thuyết, phân tích phương sai và nhiều loại phân tích thống kê khác. Điều này giúp người dùng không chỉ nắm bắt được thông tin cơ bản mà còn khai thác sâu hơn vào các yếu tố tiềm ẩn trong dữ liệu.
Một trong những đặc điểm nổi bật nhất là khả năng tạo báo cáo tự động và biểu đồ trực quan hóa dữ liệu. Những tính năng này giúp cải thiện khả năng giao tiếp dữ liệu và hỗ trợ quá trình ra quyết định.
Sự tiện lợi khi làm việc với Excel
Excel là một công cụ quen thuộc với nhiều người dùng. Việc tổ chức dữ liệu trong Excel dễ dàng hơn, giúp người dùng nhanh chóng nhập liệu và sửa đổi các giá trị. Không giống như SPSS, Excel cung cấp giao diện thân thiện với người sử dụng và cho phép thực hiện một số thao tác tính toán cơ bản ngay lập tức.
Chuyển dữ liệu từ Excel sang SPSS sẽ phát huy tối đa sức mạnh của cả hai phần mềm, giúp bạn có cái nhìn tổng quan và chính xác hơn về dữ liệu của mình.
Các ứng dụng của SPSS trong nghiên cứu
SPSS được sử dụng rộng rãi trong nghiên cứu xã hội, giáo dục, y tế, và kinh doanh. Người dùng có thể áp dụng các kỹ thuật phân tích dữ liệu để điều tra thị trường, phân tích hành vi người tiêu dùng hay nghiên cứu y tế.
Với những ứng dụng phong phú như vậy, việc biết cách chạy SPSS từ Excel sẽ mang lại lợi ích lớn cho bất kỳ ai muốn nâng cao kỹ năng phân tích dữ liệu của mình.
Cách chuẩn bị dữ liệu trên Excel trước khi đưa vào SPSS
Chuẩn bị dữ liệu Excel chạy SPSS
Trước khi bạn có thể chạy SPSS từ Excel, bạn cần phải chuẩn bị dữ liệu của mình một cách cẩn thận. Một bảng dữ liệu được chuẩn bị tốt sẽ giúp quá trình phân tích trở nên suôn sẻ và hiệu quả hơn.
Định dạng dữ liệu trong Excel
Khi làm việc với Excel, bạn cần chắc chắn rằng dữ liệu của bạn được định dạng đúng. Mỗi cột trong bảng dữ liệu đại diện cho một biến, và mỗi hàng đại diện cho một quan sát.
Bạn nên chú ý đến định dạng của các biến. Ví dụ, nếu một biến là số liệu liên quan đến tuổi, hãy đảm bảo rằng nó được định dạng là số, chứ không phải là văn bản. Điều này sẽ giúp SPSS hiểu dữ liệu của bạn một cách chính xác hơn và đảm bảo cách chạy SPSS từ Excel sẽ được áp dụng tốt.
Xóa bỏ dữ liệu thừa hoặc không cần thiết
Trước khi nhập dữ liệu vào SPSS, bạn cũng cần xem xét và loại bỏ các thông tin không cần thiết hoặc trùng lặp. Điều này không chỉ giúp bạn giảm dung lượng file mà còn tăng tính chính xác của kết quả phân tích.
Hãy sử dụng các công cụ lọc và tìm kiếm trong Excel để xác định các mục dữ liệu không hợp lệ và xóa chúng trước khi tiến hành chuyển đổi.
Kiểm tra lỗi trong dữ liệu
Một trong những bước quan trọng nhất trong quá trình chuẩn bị dữ liệu là kiểm tra lỗi. Lỗi trong dữ liệu có thể dẫn đến kết quả phân tích sai lệch. Bạn nên kiểm tra các ô trống, các giá trị không hợp lệ, và các kiểu dữ liệu không đồng nhất.
Sử dụng các công cụ phân tích trong Excel để phát hiện các vấn đề này là một lựa chọn khôn ngoan. Nếu bạn phát hiện lỗi, hãy chỉnh sửa ngay trước khi xuất dữ liệu.
Cách xuất dữ liệu từ Excel vào SPSS

Sau khi đã chuẩn bị xong dữ liệu trong Excel, bước tiếp theo là xuất nó sang SPSS để chuẩn bị cho cách chạy SPSS từ Excel. Quá trình này rất đơn giản nhưng cần chú ý đến một số chi tiết nhỏ để đảm bảo dữ liệu được chuyển giao thành công.
Bước 1: Lưu file Excel
Đầu tiên, hãy chắc chắn rằng bạn đã lưu file Excel dưới định dạng mà SPSS có thể đọc được. Thông thường, bạn nên lưu file ở định dạng “.xlsx” hoặc “.xls”.
Hãy nhớ đặt tên file một cách rõ ràng và dễ nhận biết để bạn có thể tìm thấy nó dễ dàng sau này.
Bước 2: Mở SPSS và chọn Import Data
Mở SPSS và chọn “File” > “Import Data” > “Excel”. Sau đó, bạn sẽ được yêu cầu chọn file Excel mà bạn đã lưu trước đó. Chọn file và nhấn “Open”.
Bước 3: Thiết lập thông số nhập khẩu
Tại đây, bạn sẽ thấy một cửa sổ nhập dữ liệu xuất hiện. Hãy chú ý đến các tùy chọn như “Read variable names from the first row of data” nếu bạn đã có tiêu đề cột trong file Excel.
Tiếp theo, bạn có thể tùy chỉnh các thông số như loại dữ liệu và tên biến. Điều này sẽ giúp SPSS hiểu rõ hơn về cấu trúc dữ liệu của bạn.
Bước 4: Hoàn tất quá trình nhập dữ liệu
Cuối cùng, nhấn “OK” để hoàn tất quá trình nhập liệu. SPSS sẽ hiển thị dữ liệu của bạn trong cửa sổ dữ liệu. Từ đây, bạn có thể bắt đầu thực hiện các phân tích thống kê mà bạn mong muốn và áp dụng cách chạy SPSS từ Excel mà Xulysolieu gợi ý.
Cách chạy SPSS từ Excel chi tiết
Sau khi đã nhập dữ liệu từ Excel vào SPSS, bước tiếp theo là thực hiện phân tích dữ liệu. SPSS cung cấp rất nhiều công cụ và kỹ thuật để bạn có thể khai thác thông tin từ dữ liệu của mình một cách hiệu quả.
Các loại phân tích phổ biến trong SPSS
SPSS cho phép bạn thực hiện nhiều loại phân tích khác nhau như phân tích mô tả, phân tích hồi quy, và phân tích phương sai. Mỗi loại phân tích đều có những ứng dụng cụ thể phù hợp với từng loại dữ liệu và câu hỏi nghiên cứu.
Phân tích mô tả giúp bạn có cái nhìn tổng quát về dữ liệu bằng cách tính toán các thông số như trung bình, độ lệch chuẩn, và phân vị.
Phân tích hồi quy lại giúp bạn kiểm tra mối quan hệ giữa các biến, trong khi phân tích phương sai cho phép bạn so sánh sự khác biệt giữa các nhóm dữ liệu.
Cách thực hiện một phân tích cơ bản
Để thực hiện phân tích trong SPSS, trước tiên bạn cần xác định rõ câu hỏi nghiên cứu và chọn loại phân tích phù hợp. Ví dụ, nếu bạn muốn kiểm tra mối quan hệ giữa tuổi và thu nhập, phân tích hồi quy có thể là lựa chọn tốt nhất.
Trong SPSS, bạn chỉ cần chọn “Analyze” > “Regression” > “Linear” và nhập vào các biến tương ứng. Sau đó, bạn chỉ cần nhấn “OK” để SPSS thực hiện phân tích.
Trình bày kết quả phân tích
Sau khi hoàn tất phân tích, SPSS sẽ tạo ra một bảng kết quả với các thông tin chi tiết về mô hình hồi quy, độ tin cậy, và các hệ số liên quan. Bạn có thể sử dụng các bảng này để viết báo cáo hoặc trình bày kết quả một cách trực quan.
Ngoài ra, việc tạo biểu đồ và hình ảnh minh họa cho kết quả cũng là một cách hữu ích để truyền đạt thông tin. SPSS cung cấp nhiều tùy chọn để tạo các biểu đồ khác nhau từ dữ liệu của bạn.
| Kết quả Hồi quy | Hệ số | Sai số chuẩn | p-value |
|---|---|---|---|
| Tuổi | 0.45 | 0.10 | 0.01 |
| Giới tính | 0.30 | 0.15 | 0.05 |
Các mẹo và thủ thuật khi áp dụng cách chạy SPSS từ Excel
Khi đã nắm được cơ bản cách chạy SPSS từ Excel, có một số mẹo và thủ thuật bạn nên lưu ý để tối ưu hóa quy trình phân tích của mình.
Tận dụng các tài liệu hướng dẫn và cộng đồng trực tuyến
Có rất nhiều tài liệu hướng dẫn và diễn đàn trực tuyến về SPSS. Bạn có thể tham gia các nhóm trên mạng xã hội hoặc các diễn đàn chuyên môn để trao đổi kinh nghiệm và tìm hiểu thêm về cách chạy SPSS từ Excel.
Các video hướng dẫn trên YouTube cũng là một nguồn tài nguyên quý giá, giúp bạn hình dung rõ hơn về quy trình phân tích.
Làm quen với mã lệnh SPSS
Mặc dù bạn có thể sử dụng giao diện đồ họa của SPSS, nhưng nếu bạn làm quen với mã lệnh, bạn có thể thực hiện các thao tác nhanh chóng hơn. SPSS có ngôn ngữ lập trình riêng gọi là Syntax, giúp bạn tự động hóa nhiều nhiệm vụ.
Việc lưu giữ các đoạn mã lệnh cho các phân tích thường xuyên sẽ giúp tiết kiệm thời gian đáng kể trong công việc của bạn.
Đầu tư thời gian vào việc học hỏi
SPSS là một phần mềm mạnh mẽ và có nhiều tính năng. Việc dành thời gian để tìm hiểu sâu hơn về các chức năng và cách chạy SPSS từ Excel sẽ giúp bạn cải thiện kỹ năng phân tích dữ liệu.
Hãy tham gia các khóa học online hoặc offline để tăng cường kiến thức của bạn về cách chạy SPSS từ Excel và các phương pháp phân tích thống kê.
Kết luận
Việc nắm vững cách chạy SPSS từ Excel không chỉ giúp bạn tiết kiệm thời gian mà còn nâng cao chất lượng phân tích dữ liệu của mình. Từ việc chuẩn bị dữ liệu trong Excel, xuất dữ liệu vào SPSS cho đến thực hiện các phân tích thống kê, mỗi bước đều quan trọng để đảm bảo kết quả cuối cùng chính xác và đáng tin cậy. Hy vọng rằng bài viết cách chạy SPSS từ Excel này đã cung cấp cho bạn những thông tin hữu ích và những mẹo cần thiết để bắt đầu hành trình phân tích dữ liệu của riêng mình.
Thiết kế thí nghiệm và xử lý số liệu – Khám phá quy trình
Thiết kế thí nghiệm và xử lý số liệu là hai giai đoạn thiết yếu trong bất kỳ nghiên cứu khoa học nào. Để hiểu rõ hơn về chúng, hãy cùng nhau khám phá sâu hơn vào từng khía cạnh của quá trình này.
Hiểu biết cơ bản về thiết kế thí nghiệm
Thiết kế thí nghiệm không chỉ đơn thuần là việc lên kế hoạch cho một cuộc thử nghiệm mà còn bao gồm nhiều yếu tố khác nhau để đảm bảo tính chính xác và độ tin cậy của kết quả. Để có thể tiến hành một thí nghiệm thành công, nhà nghiên cứu cần phải nắm vững các khái niệm cơ bản sau:
Mục tiêu của thí nghiệm
Một trong những khía cạnh quan trọng nhất của thiết kế thí nghiệm là xác định rõ ràng mục tiêu bạn muốn đạt được. Điều này sẽ giúp hướng dẫn toàn bộ quy trình thí nghiệm, từ việc lựa chọn phương pháp cho đến cách thức phân tích dữ liệu.
- Mục tiêu cụ thể: Làm rõ câu hỏi nghiên cứu mà bạn đang cố gắng trả lời.
- Kết quả mong đợi: Xác định những gì bạn hy vọng sẽ tìm thấy từ thí nghiệm của mình.
- Cách áp dụng: Đưa ra cách mà các kết quả có thể được áp dụng trong thực tế.
Các biến trong thí nghiệm
Trong mỗi thí nghiệm, có nhiều biến có thể ảnh hưởng đến kết quả cuối cùng. Việc phân loại và quản lý các biến này là rất quan trọng.
- Biến độc lập: Biến mà nhà nghiên cứu thay đổi để xem ảnh hưởng của nó đến kết quả.
- Biến phụ thuộc: Biến mà bạn đo lường để đánh giá tác động của biến độc lập.
- Biến kiểm soát: Những yếu tố không thay đổi trong thí nghiệm nhưng có thể ảnh hưởng đến kết quả. Việc kiểm soát các biến này giúp tăng cường độ chính xác của thí nghiệm.
Tiêu chí lựa chọn mẫu
Lựa chọn mẫu là một phần thiết yếu trong thiết kế thí nghiệm. Việc chọn mẫu không đúng có thể dẫn đến kết quả sai lệch hoặc không đại diện cho tổng thể.
- Kích thước mẫu: Kích thước mẫu lớn có thể làm tăng tính chính xác của kết quả.
- Phương pháp chọn mẫu: Có thể sử dụng các phương pháp như chọn mẫu ngẫu nhiên, chọn mẫu theo tầng hay chọn mẫu thuận tiện tùy thuộc vào mục tiêu nghiên cứu.
- Đại diện: Mẫu cần đại diện cho dân số mà bạn đang nghiên cứu để bảo đảm tính hợp lệ của thí nghiệm.
Xử lý số liệu – Nghệ thuật nhìn nhận thông tin

Sau khi quá trình thiết kế thí nghiệm hoàn tất và dữ liệu đã được thu thập, bước tiếp theo là xử lý số liệu. Đây là bước không kém phần quan trọng trong quy trình nghiên cứu. Xử lý số liệu bao gồm nhiều công đoạn, từ việc tổ chức, phân tích, đến việc trình bày dữ liệu một cách trực quan.
Tổ chức dữ liệu
Tổ chức dữ liệu là bước đầu tiên trong quá trình xử lý số liệu. Dữ liệu cần được sắp xếp một cách logic và dễ dàng truy cập để phục vụ cho việc phân tích sau này.
- Nhập dữ liệu: Sử dụng phần mềm chuyên dụng để nhập và lưu trữ dữ liệu một cách an toàn.
- Kiểm tra tính chính xác: Kiểm tra kỹ lưỡng để phát hiện lỗi hoặc sự không nhất quán trong dữ liệu.
- Chia nhỏ dữ liệu: Chia dữ liệu thành các nhóm hoặc phân loại để việc phân tích trở nên dễ dàng hơn.
Phân tích dữ liệu
Phân tích dữ liệu là giai đoạn quyết định trong xử lý số liệu, nơi mà các nhà nghiên cứu có thể rút ra kết luận từ dữ liệu đã thu thập.
- Sử dụng phần mềm thống kê: Các phần mềm như SPSS, R hoặc Python có thể hỗ trợ mạnh mẽ trong việc phân tích dữ liệu.
- Kiểm định giả thuyết: Sử dụng các phương pháp kiểm định như t-test, ANOVA để kiểm tra giả thuyết đề ra ban đầu.
- Tìm kiếm mối liên hệ: Phân tích các mối tương quan giữa các biến để hiểu rõ hơn về dữ liệu.
Trình bày dữ liệu
Cuối cùng, việc trình bày dữ liệu một cách rõ ràng và trực quan là rất quan trọng. Một báo cáo tốt không chỉ cung cấp thông tin mà còn giúp người đọc dễ dàng hiểu được những phát hiện mới.
- Sử dụng đồ thị: Các biểu đồ và đồ thị có thể minh họa dữ liệu một cách sinh động và dễ hiểu hơn.
- Báo cáo chi tiết: Cung cấp các thông tin chi tiết và giải thích rõ ràng để người đọc có thể hiểu được quy trình và kết quả nghiên cứu.
- Tóm tắt các kết quả chính: Việc tóm tắt các điểm chính giúp người đọc dễ dàng nắm bắt nội dung mà không cần phải đọc hết mọi chi tiết.
Các vấn đề thường gặp
Mặc dù thiết kế thí nghiệm và xử lý số liệu là những giai đoạn rất quan trọng, nhưng vẫn có nhiều vấn đề mà các nhà nghiên cứu có thể gặp phải trong quá trình này. Dưới đây là một số vấn đề phổ biến và cách giải quyết chúng.
Thiếu sự chuẩn bị
Một trong những vấn đề lớn nhất mà các nhà nghiên cứu thường gặp phải là thiếu sự chuẩn bị. Điều này có thể dẫn đến một loạt các vấn đề trong cả thiết kế thí nghiệm và xử lý số liệu.
- Không xác định rõ ràng mục tiêu: Nếu không có một mục tiêu rõ ràng, thí nghiệm có thể trở nên mơ hồ và không hiệu quả.
- Chọn mẫu không đại diện: Sự thiếu sót trong việc chọn mẫu có thể dẫn đến kết quả sai lệch và không phản ánh được thực tế.
- Không kiểm soát các biến: Việc không kiểm soát các biến có thể ảnh hưởng nghiêm trọng đến độ chính xác của thí nghiệm.
Lỗi trong quá trình thu thập dữ liệu
Thu thập dữ liệu là một giai đoạn khá nhạy cảm và rất dễ xảy ra lỗi. Những lỗi này có thể gây ra hậu quả nghiêm trọng cho kết quả nghiên cứu.
- Dữ liệu không chính xác: Việc nhập dữ liệu sai hoặc không chính xác có thể dẫn đến những kết luận sai lầm.
- Mất mát dữ liệu: Việc mất mát dữ liệu trong quá trình thu thập có thể làm suy giảm chất lượng của thí nghiệm.
- Khó khăn trong việc phân tích: Nếu dữ liệu không được tổ chức tốt, việc phân tích có thể trở nên khó khăn và mất thời gian.
Thiếu sự minh bạch trong báo cáo kết quả
Một vấn đề khác mà nhiều nhà nghiên cứu gặp phải là thiếu minh bạch trong việc báo cáo kết quả nghiên cứu của mình. Điều này có thể dẫn đến sự hoài nghi từ phía cộng đồng khoa học và công chúng.
- Không cung cấp đủ thông tin: Một báo cáo không đầy đủ có thể khiến người đọc khó hiểu về quy trình và kết quả nghiên cứu.
- Thiếu sự so sánh với các nghiên cứu trước: Việc không đặt kết quả vào bối cảnh rộng hơn có thể làm giảm giá trị của nghiên cứu.
- Không công khai dữ liệu: Sự thiếu minh bạch trong việc chia sẻ dữ liệu có thể gây ra nghi ngờ về độ tin cậy của kết quả.
Các ứng dụng thực tiễn của thiết kế thí nghiệm và xử lý số liệu

Thiết kế thí nghiệm và xử lý số liệu không chỉ có nghĩa trong lĩnh vực khoa học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dưới đây là một số ví dụ điển hình về ứng dụng thực tiễn của chúng.
Nghiên cứu y học
Trong lĩnh vực y học, việc thiết kế thí nghiệm và xử lý số liệu là rất quan trọng để đảm bảo hiệu quả và độ an toàn của các loại thuốc và phương pháp điều trị.
- Thử nghiệm lâm sàng: Các thử nghiệm này được thiết kế rất kĩ lưỡng để đánh giá hiệu quả của thuốc, bao gồm việc kiểm soát các biến và phân tích kết quả một cách chi tiết.
- Nghiên cứu dịch tễ học: Sử dụng các phương pháp thiết kế thí nghiệm để tìm hiểu nguyên nhân gây ra bệnh tật và cách cải thiện sức khỏe cộng đồng.
Khoa học xã hội
Trong lĩnh vực khoa học xã hội, thiết kế thí nghiệm và xử lý số liệu cũng đóng vai trò quan trọng.
- Khảo sát và nghiên cứu thị trường: Sử dụng các phương pháp khảo sát để thu thập dữ liệu từ người tiêu dùng và phân tích để đưa ra quyết định kinh doanh.
- Nghiên cứu hành vi con người: Các thí nghiệm có thể giúp các nhà nghiên cứu hiểu rõ hơn về hành vi và tâm lý con người.
Giáo dục
Trong giáo dục, thiết kế thí nghiệm và xử lý số liệu cũng có thể được áp dụng để cải thiện quá trình dạy và học.
- Đánh giá chương trình giảng dạy: Sử dụng thiết kế thí nghiệm để đánh giá hiệu quả của các chương trình giảng dạy mới.
- Nghiên cứu phương pháp giảng dạy: Các nghiên cứu có thể giúp xác định phương pháp giảng dạy nào là hiệu quả nhất cho học sinh.
Kết luận
Thiết kế thí nghiệm và xử lý số liệu là hai yếu tố vô cùng quan trọng trong nghiên cứu khoa học. Hiểu rõ quy trình và những vấn đề thường gặp sẽ giúp các nhà nghiên cứu thực hiện những nghiên cứu chính xác và đáng tin cậy hơn. Qua đó, tạo ra những hiểu biết sâu sắc và góp phần vào sự phát triển của tri thức nhân loại.
Cách chạy spss từ google form – Hướng dẫn chi tiết
Cách chạy spss từ google form là một trong những nhu cầu phổ biến của những người làm nghiên cứu, thống kê. Việc kết hợp giữa Google Form và SPSS giúp tối ưu hóa quy trình thu thập và phân tích dữ liệu, mang lại kết quả chính xác hơn.
Hướng dẫn cơ bản về Google Form
Google Form là một công cụ miễn phí được Google phát triển để tạo ra các biểu mẫu khảo sát, thu thập ý kiến hay dữ liệu một cách nhanh chóng và dễ dàng. Trong phần này, chúng ta sẽ tìm hiểu về cách sử dụng Google Form, cũng như những lợi ích mà nó mang lại cho quá trình thu thập dữ liệu.
Tạo Google Form
Để bắt đầu, bạn cần truy cập vào trang Google Forms bằng tài khoản Google của mình. Sau đó, làm theo các bước sau:
- Chọn Template hoặc Bắt đầu từ Đầu: Bạn có thể chọn một mẫu có sẵn hoặc tạo biểu mẫu mới từ đầu.
- Thêm câu hỏi: Google Form cho phép bạn thêm nhiều loại câu hỏi khác nhau như trắc nghiệm, dạng văn bản, thang điểm…
- Tùy chỉnh giao diện: Bạn có thể thay đổi màu sắc, hình nền và phông chữ để biểu mẫu trở nên hấp dẫn hơn.
- Chia sẻ biểu mẫu: Sau khi hoàn thành, bạn có thể gửi đường link qua email, mạng xã hội hoặc nhúng vào website.
Những lợi ích của việc sử dụng Google Form
Google Form không chỉ đơn thuần là một công cụ thu thập dữ liệu mà còn mang lại nhiều lợi ích cho người sử dụng:
- Miễn phí và dễ sử dụng: Người dùng không cần phải trả tiền để sử dụng, đồng thời giao diện rất trực quan.
- Tích hợp với Google Drive: Dữ liệu thu thập tự động lưu trữ trên Google Drive, giúp bạn dễ dàng quản lý và chia sẻ.
- Phân tích dữ liệu nhanh chóng: Google Form cung cấp báo cáo tóm tắt, giúp bạn có cái nhìn tổng quan về dữ liệu ngay lập tức.
Sử dụng Google Form cho nghiên cứu
Khi thực hiện nghiên cứu, việc thu thập dữ liệu là cực kỳ quan trọng. Google Form hỗ trợ bạn trong việc thiết kế những câu hỏi phù hợp với mục tiêu nghiên cứu:
- Xác định đối tượng khảo sát: Trước tiên, bạn cần xác định ai sẽ là người tham gia khảo sát. Điều này giúp tối ưu hóa nội dung câu hỏi.
- Thiết kế câu hỏi thông minh: Bạn nên đặt câu hỏi rõ ràng và dễ hiểu, tránh sự mơ hồ.
- Kiểm tra trước khi phát hành: Trước khi gửi đi, hãy kiểm tra biểu mẫu để đảm bảo mọi thứ hoạt động tốt.
Chuyển dữ liệu từ Google Form sang SPSS
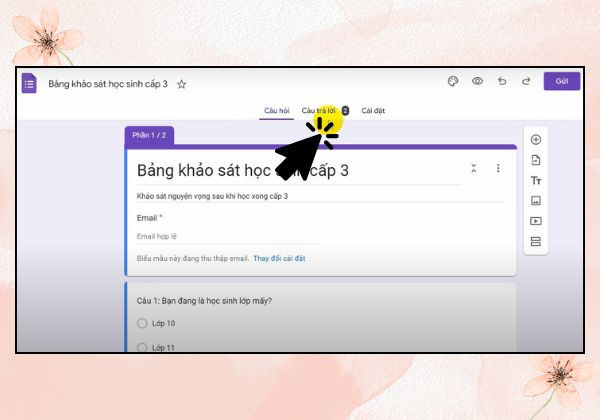
Sau khi thu thập dữ liệu từ Google Form, bước tiếp theo là chuyển dữ liệu đó sang SPSS để phân tích. Phần này sẽ hướng dẫn bạn cách thực hiện điều này một cách hiệu quả.
Xuất dữ liệu từ Google Sheets
Khi bạn đã thu thập đủ dữ liệu, hãy làm theo các bước sau để xuất dữ liệu từ Google Sheets:
- Mở Google Sheets: Mở bảng tính mà Google Form tự động tạo ra.
- Xuất dữ liệu: Chọn “Tệp” > “Tải xuống” > “Microsoft Excel (.xlsx)” hoặc “CSV”.
- Lưu file vào máy tính: Đảm bảo bạn lưu file ở nơi dễ tìm.
Nhập dữ liệu vào SPSS
Khi bạn đã có file dữ liệu, bước tiếp theo là nhập dữ liệu vào SPSS:
- Mở SPSS: Khởi động chương trình SPSS trên máy tính của bạn.
- Nhập dữ liệu: Chọn “File” > “Open” > “Data”, sau đó chọn file Excel hoặc CSV bạn vừa tải về.
- Kiểm tra dữ liệu: Sau khi nhập, hãy kiểm tra xem dữ liệu đã đúng định dạng chưa.
Làm sạch dữ liệu
Trước khi tiến hành phân tích, việc làm sạch dữ liệu là rất quan trọng:
- Khám phá dữ liệu: Xem xét các giá trị bất thường, thiếu sót hoặc lỗi.
- Loại bỏ dữ liệu lỗi: Nếu có bất kỳ hàng nào chứa dữ liệu sai, hãy xóa chúng hoặc sửa chữa nếu có thể.
- Biến đổi dữ liệu: Nếu cần thiết, bạn có thể thay đổi kiểu dữ liệu cho phù hợp với yêu cầu phân tích.
Tạo biến trong SPSS
Một bước quan trọng khác trong quy trình phân tích dữ liệu là tạo biến trong SPSS:
- Đặt tên cho biến: Đảm bảo tên biến dễ hiểu và phản ánh nội dung dữ liệu.
- Định nghĩa kiểu biến: Chọn kiểu biến phù hợp như số nguyên, số thực, chuỗi.
- Tạo mã cho biến định tính: Nếu bạn có biến định tính, hãy tạo mã để dễ dàng xử lý sau này.
Phân tích dữ liệu bằng SPSS
Sau khi dữ liệu đã được nhập và làm sạch, chúng ta sẽ tiến hành phân tích dữ liệu bằng SPSS. Phần này sẽ hướng dẫn chi tiết về các phương pháp phân tích cơ bản mà bạn có thể áp dụng.
Thống kê mô tả
Thống kê mô tả là bước đầu tiên trong phân tích dữ liệu, giúp bạn có cái nhìn tổng quát về dữ liệu:
- Tính toán các chỉ số cơ bản: Các chỉ số như trung bình, trung vị, mode, độ lệch chuẩn giúp bạn hiểu rõ hơn về tập dữ liệu.
- Sử dụng bảng và biểu đồ: SPSS cho phép bạn tạo bảng và biểu đồ để hình ảnh hóa dữ liệu, giúp việc phân tích trở nên dễ dàng hơn.
- Kiểm tra phân phối dữ liệu: Sử dụng biểu đồ histogram để kiểm tra phân phối của dữ liệu, từ đó đưa ra những nhận định ban đầu.
Phân tích tương quan
Sau khi đã có cái nhìn tổng quát, bước tiếp theo là phân tích tương quan giữa các biến:
- Tương quan Pearson: Đây là phương pháp phổ biến để xác định mối liên hệ giữa hai biến định lượng.
- Tương quan Spearman: Sử dụng khi dữ liệu không tuân theo phân phối chuẩn, giúp bạn vẫn có thể phân tích được sự liên hệ.
- Diễn giải kết quả: Khi có kết quả, bạn cần diễn giải chúng một cách cụ thể để làm rõ mối quan hệ giữa các biến.
Kiểm định giả thuyết
Kiểm định giả thuyết là một phần quan trọng trong nghiên cứu:
- Thiết lập giả thuyết: Bạn cần xác định giả thuyết null và giả thuyết thay thế trước khi thực hiện kiểm định.
- Chọn phương pháp kiểm định: Có nhiều phương pháp kiểm định như t-test, ANOVA, tùy thuộc vào loại dữ liệu và số lượng nhóm so sánh.
- Diễn giải kết quả kiểm định: Dựa trên p-value, bạn sẽ quyết định chấp nhận hay bác bỏ giả thuyết.
Tạo báo cáo
Cuối cùng, việc tạo báo cáo là một bước không thể thiếu:
- Tóm tắt kết quả: Tạo một phần tóm tắt ngắn gọn về những gì bạn đã tìm thấy.
- Sử dụng biểu đồ: Đưa vào các biểu đồ để làm nổi bật kết quả chính.
- Viết phân tích sâu: Giải thích kết quả và đưa ra những gợi ý cho các nghiên cứu sau.
Kết luận
Cách chạy spss từ google form không chỉ giúp bạn thu thập và phân tích dữ liệu một cách hiệu quả mà còn giúp bạn tiết kiệm thời gian và công sức. Qua bài viết này, chúng ta đã tìm hiểu về các bước từ việc tạo Google Form đến việc nhập dữ liệu vào SPSS và phân tích chúng. Hy vọng rằng những thông tin này sẽ hữu ích cho những ai đang muốn cải thiện khả năng nghiên cứu và phân tích dữ liệu của mình.
Cách Gộp Biến Trong SPSS – Hướng Dẫn Chi Tiết
Trong quá trình phân tích dữ liệu, việc cách gộp biến trong SPSS là một kỹ thuật quan trọng giúp chúng ta tổ chức và tinh chỉnh dữ liệu để có được những kết quả chính xác. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về phương pháp này, từ lý thuyết đến thực hành.
Tại Sao Cần Gộp Biến Trong SPSS?
Gộp biến là một thao tác làm giảm số lượng biến trong mô hình phân tích mà vẫn giữ nguyên thông tin cần thiết. Nó rất hữu ích trong nhiều trường hợp cụ thể mà chúng ta sẽ khám phá ở đây.
Tăng Tính Chính Xác Trong Phân Tích
Một trong những lý do chính mà các nhà nghiên cứu gộp biến là để tăng tính chính xác của mô hình phân tích. Khi có quá nhiều biến độc lập, điều này có thể dẫn đến hiện tượng nhiễu loạn, làm giảm độ chính xác của kết quả. Việc gộp các biến tương tự nhau lại với nhau sẽ giúp tập trung vào những yếu tố quan trọng nhất.
Đơn Giản Hóa Mô Hình
Việc gộp biến cũng giúp đơn giản hóa mô hình phân tích. Một mô hình phức tạp với nhiều biến có thể khó khăn hơn trong việc giải thích và diễn giải kết quả. Bằng cách gộp các biến có liên quan, chúng ta có thể tạo ra các chỉ số tổng hợp mà dễ dàng hơn trong việc hiểu và sử dụng.
Tối Ưu Hóa Thời Gian Phân Tích
Cuối cùng, gộp biến có thể tiết kiệm thời gian phân tích dữ liệu. Với ít biến hơn để xem xét, bạn có thể phân tích nhanh chóng và hiệu quả hơn, từ đó đưa ra quyết định kịp thời.
Các Phương Pháp Gộp Biến Trong SPSS

Có nhiều phương pháp khác nhau để gộp biến trong SPSS, mỗi phương pháp phù hợp với từng loại dữ liệu và mục tiêu phân tích khác nhau. Dưới đây là những phương pháp phổ biến nhất.
Gộp Biến Thông Qua Tính Toán Trung Bình
Phương pháp đầu tiên và đơn giản nhất là gộp biến thông qua việc tính toán trung bình. Bạn có thể gộp một loạt các biến liên quan (như điểm số từ nhiều câu hỏi khảo sát) để tạo ra một biến mới đại diện cho giá trị trung bình.
Quy Trình Thực Hiện
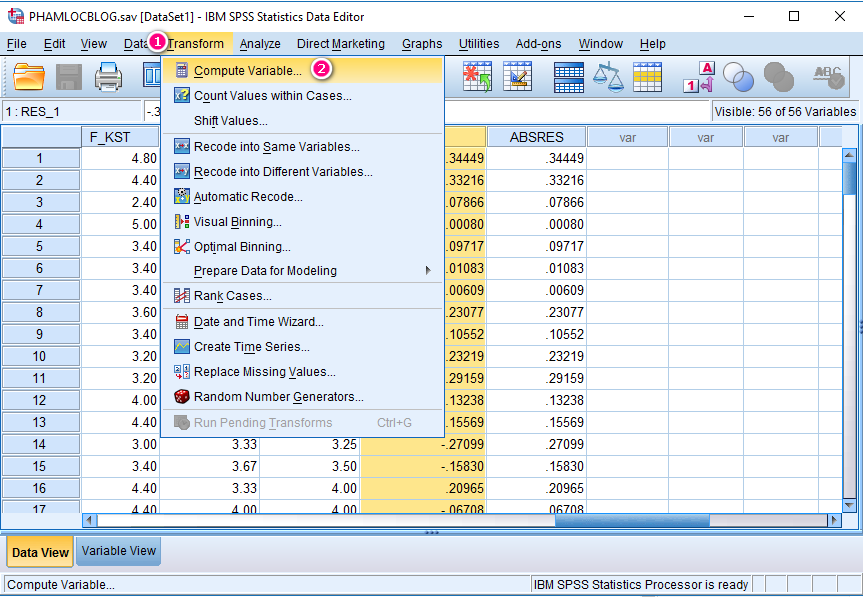
- Mở SPSS và vào menu “Transform”.
- Chọn “Compute Variable”.
- Nhập tên biến mới vào ô “Target Variable”.
- Sử dụng hàm
MEANđể tính trung bình của các biến cần gộp. Ví dụ, nếu bạn có ba biến A, B và C, cú pháp sẽ như sau:MEAN(A, B, C).
Lưu Ý Khi Sử Dụng Phương Pháp Này
Mặc dù phương pháp này đơn giản, nhưng nó có một số giới hạn. Nếu các biến có độ phân bố không giống nhau hoặc có sai lệch lớn, việc tính toán trung bình có thể không phản ánh đúng thực tế. Do đó, cần cân nhắc kỹ lưỡng trước khi áp dụng.
Sử Dụng Phân Tích Nhân Tố
Phân tích nhân tố là một phương pháp mạnh mẽ cho phép bạn gộp nhiều biến thành một hoặc vài biến tổng hợp dựa trên sự tương quan giữa các biến. Nó thường được sử dụng trong nghiên cứu xã hội học và tâm lý học.
Quy Trình Thực Hiện
- Vào menu “Analyze”, chọn “Dimension Reduction” và sau đó chọn “Factor”.
- Trong hộp thoại, thêm các biến bạn muốn phân tích vào danh sách “Variables”.
- Chọn phương pháp trích xuất (thường là Principal Components).
- Nhấn “OK” để chạy phân tích.
Lợi Ích và Hạn Chế
Lợi ích của phương pháp này là nó giúp bạn phát hiện ra các cấu trúc tiềm ẩn trong dữ liệu mà bạn có thể chưa nhận ra. Tuy nhiên, phân tích nhân tố cũng yêu cầu hiểu biết sâu sắc về thống kê và có thể khó khăn cho những người mới bắt đầu.
Gộp Biến Thông Qua Kỹ Thuật K-Means Clustering
K-Means Clustering là một phương pháp phân nhóm mà bạn có thể sử dụng để gộp các biến thành các nhóm tương tự. Phương pháp này đặc biệt có ích khi bạn có dữ liệu đa chiều.
Quy Trình Thực Hiện
- Trong SPSS, vào menu “Analyze” và chọn “Classify” rồi chọn “K-Means Cluster”.
- Xác định số lượng cụm bạn muốn tạo và thêm các biến cần thiết vào danh sách.
- Nhấn “OK” để thực hiện phân cụm.
Phân Tích Kết Quả
Sau khi thực hiện, bạn sẽ nhận được thông tin về các cụm đã được tạo ra. Bạn có thể dùng thông tin này để xây dựng các biến mới đại diện cho các cụm.
Thực Hành Gộp Biến Trong SPSS – Bước Đi Chi Tiết

Mặc dù đã nói về lý thuyết gộp biến, nhưng thực hành là phần quan trọng để hiểu rõ hơn về cách áp dụng. Dưới đây là bước đi chi tiết để bạn có thể thực hiện gộp biến trong SPSS.
Chuẩn Bị Dữ Liệu
Trước khi tiến hành gộp biến, bạn cần chuẩn bị dữ liệu của mình. Điều này bao gồm việc kiểm tra sự đầy đủ của dữ liệu và loại bỏ những giá trị ngoại lệ.
Xem Xét Dữ Liệu
Sử dụng bảng mô tả (Descriptive Statistics) để xem xét dữ liệu:
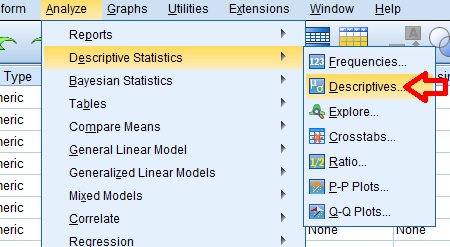
- Đi tới menu “Analyze”, chọn “Descriptive Statistics”, rồi chọn “Descriptives”.
- Thêm các biến bạn muốn xem xét và nhấn “OK”.
Làm Sạch Dữ Liệu
Kiểm tra các dữ liệu thiếu và xử lý chúng bằng các phương pháp như loại bỏ hoặc thay thế giá trị.
Tiến Hành Gộp Biến
Sau khi đã chuẩn bị dữ liệu, bạn có thể tiến hành gộp biến theo phương pháp đã chọn. Dưới đây là hướng dẫn chi tiết cho phương pháp gộp biến bằng tính toán trung bình.
Thực Hiện Gộp Biến
- Vào menu “Transform” và chọn “Compute Variable”.
- Nhập tên biến mới vào ô “Target Variable”.
- Sử dụng cú pháp
MEANđể gộp các biến.
Kiểm Tra Kết Quả Gộp Biến
Khi đã hoàn tất việc gộp biến, bạn cần kiểm tra lại kết quả. Điều này giúp đảm bảo rằng quá trình gộp biến đã diễn ra chính xác và không gây ra bất kỳ vấn đề nào trong phân tích sau này.
Sử Dụng Descriptive Statistics
Sử dụng lại chức năng “Descriptives” để xem xét biến mới được tạo ra.
Phân Tích Độ Tin Cậy
Nếu bạn gộp biến từ bảng câu hỏi, hãy sử dụng Cronbach’s Alpha để kiểm tra độ tin cậy của biến. Vào “Analyze”, chọn “Scale” và sau đó là “Reliability Analysis”.
Ghi Nhớ Những Điều Quan Trọng Khi Gộp Biến

Trong quá trình gộp biến, có một số điều quan trọng mà bạn cần phải ghi nhớ để tránh mắc phải các lỗi phổ biến.
Không Gộp Biến Ngẫu Nhiên
Việc gộp các biến không liên quan hoặc ngẫu nhiên có thể dẫn đến việc làm mất đi ý nghĩa của dữ liệu và làm giảm độ chính xác của mô hình.
Đánh Giá Tính Hợp Lý Của Các Biến
Luôn luôn đánh giá tính hợp lý của các biến trước khi gộp chúng. Bạn cần chắc chắn rằng các biến bạn định gộp có liên hệ chặt chẽ với nhau.
Theo Dõi Thay Đổi Trong Dữ Liệu
Sau khi gộp biến, hãy theo dõi sự thay đổi trong dữ liệu và kết quả phân tích. Điều này giúp bạn nhận ra những vấn đề tiềm ẩn mà có thể phát sinh từ việc gộp biến.
Kết Luận
Việc cách gộp biến trong SPSS là một quy trình quan trọng trong phân tích dữ liệu, giúp tăng cường độ chính xác và hiệu quả của mô hình. Có nhiều phương pháp gộp biến khác nhau, từ tính toán trung bình cho đến phân tích nhân tố và clustering. Việc thực hiện gộp biến đòi hỏi sự chú ý và cân nhắc đúng đắn để đạt được kết quả tốt nhất. Hy vọng bài viết này sẽ giúp bạn có cái nhìn tổng quát và hướng dẫn thực tiễn để áp dụng vào công việc phân tích dữ liệu của mình.
Cách chạy spss thang đo likert – Hướng dẫn chi tiết cho người mới bắt đầu
Trong bài viết này, chúng ta sẽ cùng nhau khám phá cách chạy spss thang đo likert một cách chi tiết và dễ hiểu. Thang đo Likert là công cụ rất phổ biến trong nghiên cứu xã hội, giúp thu thập dữ liệu về thái độ, cảm nhận của người tham gia đối với một vấn đề nào đó. Việc sử dụng SPSS để phân tích dữ liệu từ thang đo này có thể tạo ra những thông tin giá trị phục vụ cho các mục tiêu nghiên cứu.
Giới thiệu về thang đo Likert
Trước khi tìm hiểu cách chạy SPSS với thang đo Likert, chúng ta hãy bắt đầu bằng việc hiểu rõ hơn về khái niệm thang đo này.
Định nghĩa và cấu trúc thang đo Likert
Thang đo Likert thường được thiết kế dưới dạng câu hỏi với nhiều lựa chọn trả lời, ví dụ như:
- Rất không đồng ý
- Không đồng ý
- Trung lập
- Đồng ý
- Rất đồng ý
Mỗi lựa chọn sẽ tương ứng với một giá trị số nhất định, ví dụ từ 1 đến 5. Điều này giúp chuyển đổi quan điểm hoặc thái độ thành dữ liệu số để dễ dàng phân tích hơn.
Tại sao nên sử dụng thang đo Likert?
Việc sử dụng thang đo Likert đem lại nhiều lợi ích cho nghiên cứu:
- Dễ dàng thu thập dữ liệu: Người tham gia chỉ cần đánh giá theo cảm nhận của họ mà không cần phải trả lời những câu hỏi phức tạp.
- Khả năng so sánh cao: Với nhiều mức độ khác nhau, bạn có thể so sánh giữa các nhóm đối tượng hay các yếu tố khác nhau trong nghiên cứu.
- Phân tích dễ dàng: Dữ liệu từ thang đo này có thể được phân tích bằng các phần mềm thống kê như SPSS, giúp các nhà nghiên cứu đưa ra những kết luận chính xác hơn.
Những lưu ý khi xây dựng thang đo Likert
Khi thiết kế thang đo Likert, cần chú ý đến một số yếu tố như:
- Số lượng lựa chọn: Nên có ít nhất 5 lựa chọn để đảm bảo tính đa dạng trong phản hồi.
- Ngôn ngữ dễ hiểu: Câu hỏi và lựa chọn trả lời nên được viết bằng ngôn ngữ đơn giản, dễ hiểu để người tham gia có thể nắm bắt nhanh chóng.
- Tránh thiên lệch: Cần tránh các câu hỏi có hướng dẫn nhằm tránh làm ảnh hưởng đến cách trả lời của người tham gia.
Cách nhập dữ liệu vào SPSS
Sau khi đã thu thập được dữ liệu từ thang đo Likert, bước tiếp theo là nhập dữ liệu vào SPSS để tiến hành phân tích.
Chuẩn bị dữ liệu trước khi nhập
Trước khi bắt đầu nhập dữ liệu, bạn cần chuẩn bị các thông tin sau:
- Mã hóa dữ liệu: Mỗi lựa chọn trong thang đo cần được mã hóa thành một giá trị số. Ví dụ:
- Rất không đồng ý = 1
- Không đồng ý = 2
- Trung lập = 3
- Đồng ý = 4
- Rất đồng ý = 5
- Danh sách câu hỏi: Bạn cần có danh sách các câu hỏi tương ứng với các biến trong SPSS để dễ dàng thực hiện phân tích sau này.
Các bước nhập dữ liệu vào SPSS
Nhập dữ liệu vào SPSS khá đơn giản, bạn có thể làm theo các bước sau:
- Mở SPSS: Khởi động phần mềm SPSS trên máy tính của bạn.
- Tạo bảng dữ liệu mới: Vào menu
File, chọnNewvà rồiData. - Đặt tên cho các biến: Trong bảng dữ liệu, bạn cần đặt tên cho từng biến tương ứng với các câu hỏi trong thang đo Likert.
- Nhập dữ liệu: Nhấp vào ô tương ứng để nhập dữ liệu cho từng người tham gia, ghi nhớ mã hóa đã chuẩn bị trước.
Kiểm tra dữ liệu đã nhập
Sau khi nhập dữ liệu, bạn cần kiểm tra lại để đảm bảo mọi thứ đúng đắn:
- Kiểm tra lỗi nhập liệu: So sánh dữ liệu với bảng câu hỏi để phát hiện sai sót.
- Chạy thử phân tích mô tả: Sử dụng chức năng phân tích mô tả của SPSS để xem xét sự phân bố dữ liệu, từ đó đánh giá tính chính xác của việc nhập liệu.
Phân tích dữ liệu thang đo Likert bằng SPSS
Khi đã hoàn tất việc nhập dữ liệu, bước tiếp theo là thực hiện phân tích dữ liệu bằng SPSS.
Phân tích mô tả dữ liệu
Phân tích mô tả là bước đầu tiên mà bạn nên thực hiện để hiểu rõ hơn về dữ liệu của mình.
Chạy phân tích mô tả
Bạn có thể chạy phân tích mô tả theo các bước sau:
- Vào menu
Analyze, chọnDescriptive Statistics, sau đó chọnFrequencies. - Chọn các biến bạn muốn phân tích và thêm chúng vào ô
Variable(s). - Nhấn nút
OKđể xem kết quả.
Kết quả phân tích mô tả
Khi chạy phân tích mô tả, SPSS sẽ cung cấp cho bạn các thông tin như:
- Tần suất: Số lượng người tham gia ở mỗi mức độ của thang đo.
- Tỷ lệ phần trăm: Phần trăm người tham gia thuộc mỗi nhóm.
- Biểu đồ: Một số biểu đồ thống kê có thể giúp trực quan hóa kết quả.
Kiểm tra độ tin cậy của thang đo
Một trong những điều quan trọng khi làm nghiên cứu với thang đo Likert là kiểm tra độ tin cậy của bản khảo sát.
Sử dụng hệ số Cronbach’s Alpha
Hệ số Cronbach’s Alpha là công cụ phổ biến để kiểm tra độ tin cậy:
- Vào menu
Analyze, chọnScale, sau đó chọnReliability Analysis. - Chọn các biến bạn muốn kiểm tra và thêm chúng vào ô
Items. - Nhấn nút
OKđể xem kết quả.
Kết quả kiểm tra độ tin cậy
Khi thực hiện kiểm tra độ tin cậy, bạn sẽ nhận được giá trị Cronbach’s Alpha. Nếu giá trị này lớn hơn 0.7, thang đo của bạn được coi là có độ tin cậy tốt.
Phân tích mối quan hệ giữa các biến
Sau khi đã thực hiện phân tích mô tả và kiểm tra độ tin cậy, bước tiếp theo là phân tích mối quan hệ giữa các biến.
Sử dụng phân tích tương quan
Một trong những phương pháp phổ biến để phân tích mối quan hệ giữa các biến là sử dụng phân tích tương quan:
- Vào menu
Analyze, chọnCorrelate, sau đó chọnBivariate. - Chọn các biến bạn muốn phân tích và thêm chúng vào ô
Variables. - Nhấn nút
OKđể xem kết quả.
Kết quả phân tích tương quan
Khi chạy phân tích tương quan, bạn sẽ thấy giá trị hệ số tương quan (r). Giá trị này cho biết mức độ mạnh yếu của mối quan hệ giữa các biến:
- Giá trị gần 1: Mối quan hệ dương mạnh.
- Giá trị gần -1: Mối quan hệ âm mạnh.
- Giá trị gần 0: Không có mối quan hệ.
Trình bày kết quả phân tích dữ liệu

Khi đã hoàn tất quá trình phân tích, bước cuối cùng là trình bày kết quả một cách rõ ràng và dễ hiểu.
Cách tạo báo cáo trong SPSS
SPSS cung cấp nhiều tùy chọn để bạn có thể tạo báo cáo chuyên nghiệp:
- Sử dụng Output Viewer: SPSS sẽ tự động mở một cửa sổ Output để hiển thị kết quả phân tích. Bạn có thể sao chép và dán những kết quả quan trọng vào tài liệu báo cáo của mình.
- Xuất khẩu dữ liệu: Bạn có thể xuất khẩu các bảng và biểu đồ sang định dạng Excel hoặc Word để dễ dàng chỉnh sửa và trình bày hơn.
Một số mẹo trình bày kết quả
Khi trình bày kết quả phân tích, hãy chú ý đến một số yếu tố sau:
- Rõ ràng và ngắn gọn: Không nên trình bày quá nhiều thông tin mà hãy tập trung vào những gì quan trọng nhất.
- Sử dụng biểu đồ: Các biểu đồ có thể giúp dễ dàng hình dung dữ liệu hơn là chỉ dùng văn bản.
- Cung cấp bối cảnh: Khi trình bày kết quả, hãy chắc chắn rằng bạn cung cấp đủ bối cảnh để người đọc có thể hiểu rõ hơn ý nghĩa của dữ liệu.
Ví dụ về trình bày kết quả
Một ví dụ đơn giản về cách trình bày kết quả phân tích dữ liệu từ thang đo Likert có thể bao gồm:
- Tổng hợp tần suất: “Trong số 100 người tham gia, 60% cho biết họ đồng ý với câu hỏi A.”
- Biểu đồ: Kèm theo một biểu đồ cột thể hiện tỷ lệ phần trăm của từng mức độ đồng ý.
- Phân tích tương quan: “Có một mối quan hệ dương mạnh giữa câu hỏi A và B với hệ số tương quan là 0.85.”
Kết luận
Tóm lại, việc áp dụng cách chạy spss thang đo likert là một quy trình quan trọng trong nghiên cứu xã hội học. Qua việc tìm hiểu thang đo này, từ việc nhập dữ liệu đến phân tích và trình bày kết quả, bạn có thể khai thác tối đa sức mạnh của dữ liệu để đưa ra những kết luận chính xác và đáng tin cậy. Hy vọng rằng những hướng dẫn trong bài viết này sẽ giúp bạn tự tin hơn trong việc sử dụng SPSS để phân tích thang đo Likert trong các nghiên cứu của mình.
Cách chạy spss nghiên cứu khoa học – Hướng dẫn chi tiết
Cách chạy spss nghiên cứu khoa học là một trong những kỹ năng quan trọng đối với sinh viên và các nhà nghiên cứu trong lĩnh vực khoa học xã hội và nhân văn. Phần mềm SPSS (Statistical Package for the Social Sciences) không chỉ giúp phân tích dữ liệu mà còn cung cấp những công cụ mạnh mẽ để hiểu sâu về các hiện tượng xã hội, hành vi con người và nhiều khía cạnh khác trong nghiên cứu khoa học. Bài viết này sẽ hướng dẫn bạn cách sử dụng SPSS từ cơ bản đến nâng cao, bao gồm cả quy trình cài đặt, nhập liệu, xử lý số liệu, thực hiện các phân tích thống kê, và cuối cùng là cách trình bày kết quả một cách hiệu quả.
Giới thiệu về phần mềm SPSS
Trong phần này, chúng ta sẽ khám phá tổng quan về phần mềm SPSS, tại sao nó lại trở thành một công cụ phổ biến trong nghiên cứu khoa học.
Lịch sử phát triển của SPSS
Phần mềm SPSS được phát triển vào năm 1968 bởi Norman H. Nie, C. Hadlai Hull, và William G. Goodman. Ban đầu, SPSS được thiết kế riêng cho việc phân tích dữ liệu xã hội và đã nhanh chóng trở thành tiêu chuẩn vàng trong ngành thống kê.
Ngày nay, SPSS đã được IBM mua lại và tiếp tục phát triển, cung cấp nhiều tính năng nổi bật như phân tích hồi quy, phân tích phương sai (ANOVA), phân tích nhân tố, và nhiều hơn nữa. SPSS hiện có mặt trên nhiều hệ điều hành và dễ dàng tải xuống từ trang web chính thức của IBM.
Tính năng nổi bật của SPSS
SPSS cung cấp nhiều tính năng đáng chú ý, bao gồm:
- Phân tích dữ liệu: Bạn có thể thực hiện nhiều loại phân tích khác nhau như phân tích mô tả, phân tích hồi quy, kiểm định giả thuyết, và phân tích phương sai.
- Quản lý dữ liệu: SPSS cho phép bạn nhập liệu từ nhiều nguồn khác nhau như Excel, CSV, và các cơ sở dữ liệu. Việc quản lý dữ liệu cũng rất đơn giản với khả năng lọc và sắp xếp.
- Trình bày kết quả: SPSS hỗ trợ xuất báo cáo dưới dạng biểu đồ, bảng và tài liệu Word, giúp trình bày kết quả một cách trực quan và dễ hiểu.
Ai nên sử dụng SPSS?
SPSS là công cụ lý tưởng cho:
- Sinh viên chuyên ngành khoa học xã hội, tâm lý học, giáo dục, kinh tế và các ngành liên quan.
- Các nhà nghiên cứu cần phân tích dữ liệu cho các dự án nghiên cứu của họ.
- Các chuyên gia trong lĩnh vực marketing, y tế và quản lý muốn áp dụng phân tích thống kê trong công việc của mình.
Quy trình cài đặt và làm quen với SPSS
Cài đặt SPSS và làm quen với giao diện sử dụng là bước đầu tiên mà bất kỳ người dùng nào cũng cần trải qua.
Hướng dẫn cài đặt SPSS
Để cài đặt SPSS, bạn cần thực hiện các bước sau:
- Tải xuống phần mềm: Truy cập trang web IBM và tìm kiếm phiên bản SPSS phù hợp với hệ điều hành của bạn. Có thể chọn phiên bản dùng thử miễn phí hoặc mua bản quyền.
- Cài đặt: Chạy file cài đặt và làm theo hướng dẫn trên màn hình. Trong quá trình cài đặt, bạn sẽ được yêu cầu chọn thư mục lưu trữ và các tùy chọn bổ sung.
- Kích hoạt bản quyền: Nếu bạn mua bản quyền, hãy nhập mã kích hoạt khi được yêu cầu. Điều này sẽ giúp bạn truy cập đầy đủ tất cả các tính năng của SPSS.
Làm quen với giao diện SPSS
Sau khi cài đặt hoàn tất, bạn cần làm quen với giao diện người dùng của SPSS:
- Menu chính: Tại đây, bạn có thể tìm thấy các chức năng cơ bản như File, Edit, View, Data, Analyze… Mỗi mục sẽ mở ra các tùy chọn tương ứng.
- Data View và Variable View: Data View là nơi bạn nhập và xem dữ liệu, trong khi Variable View cho phép bạn chỉnh sửa thuộc tính của từng biến.
- Output Viewer: Đây là nơi hiển thị các kết quả phân tích của bạn, bao gồm bảng và biểu đồ.
Một số mẹo hữu ích khi sử dụng SPSS
- Sử dụng Help: SPSS có một hệ thống hỗ trợ rất tốt. Bạn có thể nhấn F1 để tìm hiểu thêm về bất kỳ tính năng nào.
- Lưu trữ dữ liệu thường xuyên: Để tránh mất dữ liệu, hãy thường xuyên lưu lại công việc của bạn.
- Thực hành thường xuyên: Thực hành là chìa khóa để thành thạo SPSS. Hãy thử thực hiện các bài tập khác nhau để nâng cao kỹ năng của mình.
Nhập liệu và xử lý dữ liệu bằng SPSS

Việc nhập liệu và xử lý dữ liệu là rất quan trọng trong nghiên cứu. Bước này giúp đảm bảo rằng dữ liệu của bạn được tổ chức và sẵn sàng cho phân tích.
Nhập liệu vào SPSS
Có nhiều cách để nhập dữ liệu vào SPSS, bao gồm:
- Nhập thủ công: Bạn có thể nhập dữ liệu trực tiếp vào Data View. Tuy nhiên, nếu bạn có lượng dữ liệu lớn, cách này không phải là lựa chọn tốt nhất.
- Import từ file Excel hoặc CSV: Để nhập dữ liệu từ file Excel, bạn chỉ cần chọn File -> Open -> Data và chọn file. SPSS sẽ tự động nhận diện các biến.
- Kết nối cơ sở dữ liệu: Nếu dữ liệu của bạn nằm trong cơ sở dữ liệu, SPSS cho phép bạn kết nối trực tiếp và lấy dữ liệu một cách dễ dàng.
Xử lý dữ liệu trước khi phân tích
Trước khi tiến hành phân tích, bạn cần xử lý dữ liệu để đảm bảo tính chính xác và độ tin cậy:
- Kiểm tra thiếu sót dữ liệu: Sử dụng các hàm như
FREQUENCIESđể tìm ra giá trị bị thiếu và quyết định cách xử lý, chẳng hạn như loại bỏ hoặc thay thế. - Mã hóa dữ liệu định tính: Khi làm việc với biến định tính, bạn cần mã hóa chúng thành các giá trị số để dễ dàng phân tích.
- Chỉnh sửa giá trị bất thường: Kiểm tra các giá trị ngoại lai và quyết định xem có nên loại bỏ chúng hay không. Các giá trị này có thể ảnh hưởng lớn đến kết quả phân tích.
Tổ chức dữ liệu trong SPSS
Một khi bạn đã nhập và xử lý dữ liệu, việc tổ chức dữ liệu là rất quan trọng:
- Đặt tên cho biến rõ ràng: Tên biến nên ngắn gọn nhưng mô tả đúng nội dung của biến đó.
- Thiết lập thuộc tính biến: Trong Variable View, bạn có thể thiết lập các thuộc tính như kiểu dữ liệu, độ dài, nhãn, và giá trị thiếu.
- Lưu trữ dữ liệu an toàn: Đảm bảo rằng bạn luôn lưu lại dữ liệu đã xử lý để có thể dễ dàng quay lại khi cần thiết.
Phân tích dữ liệu với SPSS
Sau khi đã có dữ liệu sạch và được tổ chức hợp lý, bước tiếp theo là thực hiện các phân tích dữ liệu với SPSS.
Các loại phân tích thông dụng
SPSS hỗ trợ nhiều loại phân tích khác nhau. Dưới đây là một số phân tích phổ biến:
- Phân tích mô tả: Giúp tóm tắt và miêu tả các đặc điểm chính của dữ liệu thông qua các chỉ số như trung bình, trung vị, độ lệch chuẩn.
- Kiểm định giả thuyết: SPSS cho phép bạn thực hiện các kiểm định thống kê như t-test, ANOVA, và Chi-square để xác định sự khác biệt giữa các nhóm.
- Phân tích hồi quy: Để tìm hiểu mối quan hệ giữa các biến, phân tích hồi quy là một công cụ mạnh mẽ. Bạn có thể thực hiện hồi quy tuyến tính hoặc hồi quy logistic tùy thuộc vào dữ liệu của mình.
Thực hiện phân tích trong SPSS
Để thực hiện một phân tích, bạn có thể làm theo các bước sau:
- Chọn loại phân tích: Từ menu Analyze, chọn loại phân tích mà bạn muốn thực hiện.
- Chọn biến cần phân tích: Kéo và thả các biến vào các ô tương ứng trong hộp thoại phân tích.
- Thiết lập tùy chọn: Với mỗi loại phân tích, bạn có thể tùy chỉnh các tùy chọn như mức ý nghĩa (alpha), phương pháp nhập biến, và nhiều tùy chọn khác.
- Chạy phân tích: Nhấn OK và SPSS sẽ thực hiện phân tích. Kết quả sẽ hiển thị trong Output Viewer.
Đọc và giải thích kết quả phân tích
Khi bạn đã có kết quả từ phân tích, bước tiếp theo là đọc và giải thích chúng:
- Hiểu các bảng kết quả: SPSS tạo ra nhiều bảng kết quả khác nhau, mỗi bảng chứa thông tin cụ thể về phân tích đã thực hiện. Nắm rõ từng bảng là rất quan trọng.
- Xem xét giá trị p: Trong hầu hết các phân tích, giá trị p sẽ cho bạn biết liệu có đủ bằng chứng để bác bỏ giả thuyết null hay không. Nếu p < 0.05, bạn có thể kết luận rằng có sự khác biệt có ý nghĩa thống kê.
- Diễn giải các yếu tố ảnh hưởng: Nếu bạn thực hiện hồi quy, hãy xem xét các hệ số hồi quy và độ tin cậy của mô hình để hiểu rõ hơn về mối quan hệ giữa các biến.
Trình bày kết quả nghiên cứu

Cuối cùng nhưng không kém phần quan trọng, việc trình bày kết quả nghiên cứu một cách hiệu quả là điều cần thiết.
Cách trình bày kết quả trong báo cáo
Trong một báo cáo nghiên cứu, phần trình bày kết quả thường cần tuân theo những nguyên tắc cụ thể:
- Rõ ràng và súc tích: Kết quả nên được trình bày một cách rõ ràng và súc tích, không nên làm rối trí người đọc với quá nhiều thông tin không cần thiết.
- Sử dụng biểu đồ và bảng: Đôi khi, hình ảnh nói lên nhiều hơn ngàn lời. Sử dụng biểu đồ, bảng và đồ thị để minh họa kết quả của bạn sẽ giúp người đọc dễ dàng hiểu hơn.
- Trích dẫn các kết quả chính: Đừng quên nhấn mạnh các kết quả chính trong phần tóm tắt của báo cáo. Những thông tin này sẽ giúp người đọc nắm bắt nhanh các điểm mấu chốt.
Định dạng báo cáo nghiên cứu
- Bố cục: Một báo cáo nghiên cứu thường bao gồm các phần như Giới thiệu, Phương pháp, Kết quả, và Thảo luận. Đảm bảo rằng bạn tuân theo định dạng mà trường học hoặc tổ chức của bạn yêu cầu.
- Phong cách viết: Sử dụng ngôn ngữ khoa học, tránh sử dụng từ ngữ lóng và đảm bảo rằng mọi câu đều có ý nghĩa.
- Kiểm tra chính tả và ngữ pháp: Trước khi nộp báo cáo, hãy chắc chắn rằng bạn đã kiểm tra kỹ các lỗi chính tả và ngữ pháp để tránh gây ấn tượng xấu với người đọc.
Sử dụng công cụ hỗ trợ trình bày
- Công cụ vẽ biểu đồ: SPSS cho phép bạn tạo biểu đồ và đồ thị trực tiếp từ kết quả phân tích, nhưng bạn cũng có thể sử dụng các công cụ khác như Excel hoặc các phần mềm vẽ biểu đồ chuyên nghiệp để tạo hình ảnh đẹp mắt hơn.
- Trình diễn kết quả: Nếu bạn cần thuyết trình về kết quả nghiên cứu, hãy chuẩn bị slide PowerPoint hoặc Prezi để truyền đạt thông tin một cách hiệu quả.
Kết luận
Cách chạy spss nghiên cứu khoa học không chỉ là việc sử dụng phần mềm để phân tích dữ liệu; đó còn là một quy trình đầy nghệ thuật và khoa học mà mỗi nhà nghiên cứu cần nắm vững. Qua bài viết này, chúng ta đã tìm hiểu từ những kiến thức cơ bản về SPSS, quy trình cài đặt, nhập liệu, xử lý và phân tích dữ liệu, cho đến cách trình bày kết quả một cách hiệu quả. Hy vọng rằng những thông tin này sẽ giúp bạn tự tin hơn trong hành trình nghiên cứu của mình, từ đó đưa ra những kết quả chất lượng và ý nghĩa cho công việc nghiên cứu khoa học.
Khám Phá Thống Kê Tần Số SPSS – Công Cụ Đắc Lực Cho Phân Tích Dữ Liệu
Trong thế giới hiện đại, việc phân tích và trình bày dữ liệu là một yếu tố không thể thiếu trong mọi lĩnh vực. Thống kê tần số SPSS giúp chúng ta có cái nhìn tổng quan và chi tiết hơn về các tập dữ liệu mà chúng ta đang làm việc với. Qua bài viết này, chúng ta sẽ cùng nhau khám phá các khía cạnh khác nhau của thống kê tần số trong SPSS, từ cơ sở lý thuyết cho đến ứng dụng thực tế.
Ý Nghĩa Của Thống Kê Tần Số Trong Nghiên Cứu
Trước khi đi sâu vào ứng dụng cụ thể, chúng ta cần hiểu rõ ý nghĩa cơ bản của thống kê tần số trong nghiên cứu.
Định Nghĩa Thống Kê Tần Số
Thống kê tần số là phương pháp dùng để mô tả phân phối của một biến bằng cách đếm số lần xuất hiện của từng giá trị trong tập dữ liệu. Điều này giúp nhà nghiên cứu nắm bắt được tình hình chung của dữ liệu cũng như phát hiện ra các xu hướng nổi bật.
Vai Trò Trong Nghiên Cứu
Thống kê tần số đóng vai trò quan trọng trong việc phân tích dữ liệu. Nó tạo ra nền tảng cho các phương pháp phân tích nâng cao hơn, chẳng hạn như phân tích hồi quy hay phân tích tương quan. Nhờ vào việc xác định phân bố của các biến, nhà nghiên cứu có thể đưa ra những giải thích và dự đoán chính xác hơn.
Ứng Dụng Thực Tế
Trong thực tế, thống kê tần số thường được ứng dụng trong nhiều lĩnh vực như y học, xã hội học, kinh tế học… Ví dụ, trong ngành y tế, bác sĩ có thể sử dụng thống kê tần số để theo dõi sự xuất hiện của các triệu chứng bệnh lý trong một nhóm bệnh nhân.
Cách Thực Hiện Thống Kê Tần Số Bằng SPSS
Để thực hiện thống kê tần số SPSS, người sử dụng cần nắm vững các bước cơ bản. Trong phần này, chúng ta sẽ tìm hiểu quy trình làm việc với SPSS từ khâu nhập dữ liệu đến khâu phân tích.
Nhập Dữ Liệu Vào SPSS
Bước đầu tiên trong quá trình phân tích là nhập dữ liệu. SPSS hỗ trợ nhiều định dạng dữ liệu khác nhau, bao gồm cả Excel và CSV. Người dùng cần chú ý đến việc cấu trúc dữ liệu sao cho phù hợp.
Việc nhập liệu có thể được thực hiện theo nhiều cách:
- Nhập trực tiếp từ bảng tính SPSS.
- Nhập từ tệp dữ liệu khác.
- Sử dụng tính năng kéo và thả để dễ dàng đưa dữ liệu vào hệ thống.
Thiết Lập Biến Cần Phân Tích
Sau khi đã nhập dữ liệu vào SPSS, bước tiếp theo là thiết lập biến mà bạn muốn phân tích. Bạn có thể chọn loại biến như biến danh nghĩa (nominal) hoặc biến thứ tự (ordinal) tùy thuộc vào mục tiêu phân tích của mình.
Các bước thiết lập biến bao gồm:
- Chọn biến trong bảng dữ liệu.
- Xác định kiểu dữ liệu: số lượng, văn bản hay ngày tháng.
- Đặt tên cho biến để dễ nhận diện.
Thực Hiện Phân Tích Tần Số
Khi biến đã được thiết lập, bạn có thể tiến hành phân tích tần số. Từ menu chính của SPSS, bạn có thể truy cập vào phần “Analyze” và chọn “Descriptive Statistics”, sau đó là “Frequencies”.
Quá trình phân tích sẽ bao gồm:
- Chọn biến cần phân tích.
- Thiết lập các tùy chọn hiển thị kết quả.
- Chạy phân tích và xem xét kết quả.
Kết quả phân tích sẽ cung cấp thông tin về tần suất xuất hiện của từng giá trị trong biến đã chọn.
Tính Toán Và Trình Bày Kết Quả Thống Kê Tần Số
Sau khi thực hiện phân tích tần số, việc tiếp theo là hiểu và trình bày kết quả một cách hiệu quả.
Cách Đọc Kết Quả Từ SPSS
Kết quả của phân tích tần số thường được trình bày dưới dạng bảng và biểu đồ. Bảng sẽ cho bạn biết cụ thể số lượng và tỷ lệ phần trăm của mỗi giá trị trong biến.
Ví dụ, bảng kết quả có thể trông như sau:
| Giá trị | Tần suất | Tỷ lệ phần trăm |
|---|---|---|
| A | 50 | 25% |
| B | 100 | 50% |
| C | 30 | 15% |
| D | 20 | 10% |
Nhìn vào bảng trên, bạn có thể nhanh chóng thấy rằng giá trị B là phổ biến nhất trong dữ liệu.
Trình Bày Kết Quả Một Cách Hiệu Quả
Việc trình bày kết quả là rất quan trọng. Bảng, biểu đồ, hoặc đồ thị sẽ giúp bạn truyền tải thông tin một cách trực quan và dễ hiểu hơn. Một biểu đồ tròn hoặc biểu đồ cột có thể giúp làm nổi bật sự khác biệt giữa các giá trị.
- Biểu đồ tròn: Thể hiện tỷ lệ phần trăm của mỗi giá trị so với tổng thể.
- Biểu đồ cột: So sánh số lượng các giá trị một cách rõ rệt.
Phân Tích Kết Quả
Phân tích kết quả là bước cuối cùng. Đây là lúc bạn đưa ra các suy luận hoặc kết luận từ dữ liệu đã phân tích. Hãy thử đặt câu hỏi:
- Những giá trị nào là nổi bật?
- Có sự khác biệt nào đáng kể giữa các nhóm không?
- Mối liên hệ nào có thể tồn tại giữa các biến?
Thông qua quá trình này, bạn có thể tìm ra những mẫu hình hoặc xu hướng và đưa ra các khuyến nghị phù hợp.
Các Lưu Ý Khi Sử Dụng Thống Kê Tần Số Trong SPSS
Mặc dù thống kê tần số SPSS mang lại nhiều lợi ích, nhưng vẫn có một số lưu ý mà người dùng cần phải nhớ.
Độ Chính Xác Của Dữ Liệu
Độ chính xác của dữ liệu đầu vào là rất quan trọng. Nếu dữ liệu bị sai lệch hoặc không đầy đủ, kết quả phân tích sẽ không phản ánh đúng thực trạng. Do đó, việc kiểm tra và làm sạch dữ liệu trước khi phân tích là điều cần thiết.
Định Nghĩa Rõ Ràng Về Biến
Người dùng cần phải định nghĩa rõ ràng các biến và phân loại chúng một cách chính xác. Việc này sẽ giúp cho quá trình phân tích trở nên dễ dàng hơn, đồng thời giảm thiểu nhầm lẫn trong việc diễn giải kết quả.
Không Quá Tin Vào Kết Quả
Cuối cùng, hãy nhớ rằng các kết quả phân tích chỉ là một phần của bức tranh lớn. Việc đánh giá các kết quả cần phải được thực hiện cẩn thận, kết hợp với các phương pháp phân tích khác để đảm bảo tính chính xác và toàn diện trong nghiên cứu.
Kết Luận
Thống kê tần số SPSS là một công cụ mạnh mẽ trong việc phân tích và trình bày dữ liệu. Qua bài viết này, chúng ta đã cùng nhau khám phá ý nghĩa của thống kê tần số, quy trình thực hiện trong SPSS, cách đọc và trình bày kết quả, cũng như các lưu ý cần thiết khi sử dụng công cụ này. Hy vọng rằng những kiến thức này sẽ giúp bạn áp dụng hiệu quả hơn trong các dự án nghiên cứu của mình.