Trong thế giới nghiên cứu khoa học hiện đại, việc phân tích dữ liệu một cách chính xác và sâu sắc đóng vai trò vô cùng quan trọng để đưa ra những kết luận xác thực và có giá trị thực tiễn cao. Một trong những phương pháp phổ biến và hiệu quả để khám phá cấu trúc tiềm ẩn trong dữ liệu chính là phân tích nhân tố khám phá (EFA). Vậy, efa là gì? Và tại sao nó lại trở thành công cụ không thể thiếu trong các nghiên cứu khoa học, đặc biệt trong các lĩnh vực như quản trị, tâm lý, xã hội học hay kinh tế? Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu chi tiết về khái niệm, vai trò, nguyên lý hoạt động, các điều kiện áp dụng cùng cách thực hiện EFA trong phần mềm SPSS một cách dễ hiểu và đầy đủ nhất.
Mục lục
ToggleGiới thiệu về phân tích nhân tố khám phá EFA
Tổng quan về phân tích nhân tố khám phá EFA
Phân tích nhân tố khám phá (Exploratory Factor Analysis – EFA) là một kỹ thuật thống kê được sử dụng rộng rãi trong nghiên cứu định lượng nhằm khám phá cấu trúc tiềm ẩn giữa các biến quan sát. Điểm đặc biệt quan trọng của EFA là khả năng đánh giá hai loại giá trị thiết yếu trong thang đo: giá trị hội tụ (convergent validity) và giá trị phân biệt (discriminant validity). Đây là hai tiêu chí then chốt giúp đảm bảo rằng các biến đo lường trong nghiên cứu đang phản ánh chính xác các khái niệm lý thuyết và phân biệt rõ ràng giữa các khái niệm khác nhau.
Thay vì chỉ dựa vào trực giác hoặc kinh nghiệm chủ quan, EFA cung cấp một phương pháp khách quan để rút gọn số lượng biến, đồng thời khám phá các nhân tố tiềm ẩn cấu thành nên dữ liệu. Nhờ đó, các nhà nghiên cứu có thể xác định được cấu trúc nội tại của tập hợp biến đo lường, phát hiện những nhóm biến có mối liên hệ chặt chẽ và gộp chúng thành các nhân tố đại diện có ý nghĩa về mặt lý thuyết.
Không dừng lại ở việc giúp xử lý dữ liệu hiệu quả hơn, EFA còn có vai trò quan trọng trong việc kiểm tra độ tin cậy và độ hợp lệ của thang đo. Phân tích này hỗ trợ quá trình thiết kế, điều chỉnh và cải thiện các thang đo nghiên cứu, từ đó tạo tiền đề vững chắc cho các bước phân tích chuyên sâu hơn như phân tích nhân tố khẳng định (CFA) hay mô hình cấu trúc tuyến tính (SEM).
Trong thực tiễn, EFA được ứng dụng phổ biến trong nhiều lĩnh vực như quản trị, tâm lý học, kinh tế, giáo dục và xã hội học. Ví dụ, trong nghiên cứu mức độ hài lòng của khách hàng, EFA giúp xác định các nhóm yếu tố chính như giá trị sản phẩm, dịch vụ chăm sóc, giá cả hay cảm nhận thương hiệu – từ đó làm cơ sở để xây dựng mô hình phân tích tiếp theo. Tương tự, trong các nghiên cứu xã hội học, EFA có thể khám phá những yếu tố nền tảng cấu thành nên các khái niệm trừu tượng như động lực cá nhân, lòng tin xã hội hay hành vi tiêu dùng.
Tóm lại, EFA không chỉ là công cụ phân tích dữ liệu, mà còn là chìa khóa để đánh giá tính hợp lệ của thang đo, từ đó cung cấp một cái nhìn toàn diện, logic và sâu sắc về các cấu trúc tiềm ẩn trong tập dữ liệu nghiên cứu.
Vai trò của EFA trong nghiên cứu khoa học
Trong nghiên cứu khoa học, việc lựa chọn đúng phương pháp phân tích phụ thuộc rất nhiều vào mục tiêu, tính chất của dữ liệu và đặc điểm của các biến đo lường. EFA mang lại những lợi ích rõ ràng trong quá trình này, đặc biệt là khả năng đánh giá độ tin cậy của thang đo, xác định các cấu trúc tiềm ẩn còn ẩn chứa trong dữ liệu, cũng như giúp các nhà nghiên cứu loại bỏ các biến thừa, giảm thiểu độ phức tạp và tăng khả năng giải thích của mô hình.
Một trong những công dụng nổi bật của EFA chính là giúp kiểm tra tính hợp lệ của các thang đo bằng chỉ số Cronbach Alpha, từ đó xác định xem các biến có thực sự đo lường đúng các khái niệm cần thiết hay không. Bên cạnh đó, việc khám phá ra các yếu tố tiềm ẩn còn giúp mô hình trở nên rõ ràng hơn, dễ hiểu hơn, từ đó tạo điều kiện thuận lợi cho các bước phân tích tiếp theo như phân tích hồi quy, mô hình cấu trúc hay các phân tích phức tạp khác. EFA còn đóng vai trò trung gian trong quá trình thiết kế nghiên cứu, giúp các nhà nghiên cứu điều chỉnh các biến đo lường, đảm bảo chúng phản ánh đúng các khái niệm cốt lõi của đề tài.
Hơn nữa, vai trò của EFA còn thể hiện rõ trong việc tối ưu hóa mô hình, đem lại các nhân tố có ý nghĩa thống kê cao, phù hợp và dễ diễn giải. Những nhân tố này sau đó có thể được dùng làm biến độc lập trong các mô hình dự báo hoặc phân tích sâu hơn, giảm thiểu khả năng bị đa cộng tuyến, góp phần nâng cao độ chính xác của kết quả nghiên cứu. Với khả năng rút gọn và làm rõ cấu trúc của dữ liệu, EFA đã trở thành công cụ không thể thiếu trong nghiên cứu khoa học đương đại, mở ra cơ hội khám phá những nội dung sâu hơn, toàn diện hơn của các tập hợp biến đo lường phức tạp.
Thế nào là nhân tố khám phá EFA?

Định nghĩa và nguyên lý hoạt động của EFA
Bạn có biết rằng EFA là phương pháp phân tích dựa trên mối quan hệ tương quan giữa các biến? Chính nhờ nguyên lý này, EFA giúp khám phá ra các yếu tố tiềm ẩn – những nhân tố nằm ẩn phía sau các biến đo lường, mà không phải lúc nào chúng ta cũng dễ dàng nhận biết. Khi áp dụng EFA, dữ liệu ban đầu của bạn gồm nhiều biến quan sát được xem như một hệ thống phức tạp, chứa đựng các cấu trúc nội tại chưa rõ ràng.
Nguyên lý hoạt động của EFA dựa trên việc phân tích ma trận tương quan giữa các biến để phát hiện ra các nhóm biến có mối liên hệ chặt chẽ với nhau. Qua đó, nó xác định các nhân tố tiềm ẩn, mỗi nhân tố đại diện cho một khái niệm hoặc yếu tố cấu thành tổng thể của dữ liệu. Phương pháp này giúp loại bỏ các biến thừa, tập trung vào các yếu tố chính và trung tâm, từ đó làm rõ cấu trúc dưới dạng các nhân tố cốt lõi, phản ánh đúng nội dung và ý nghĩa của đối tượng nghiên cứu.
Một điểm đặc biệt của EFA chính là khả năng giảm số lượng biến đo lường mà vẫn duy trì được gần như toàn bộ thông tin cần thiết để mô tả tập hợp dữ liệu ban đầu. Ví dụ, thay vì 20 biến đo lường nhỏ, sau EFA ta có thể chỉ tập trung vào 4-5 nhân tố chính, mỗi nhân tố này gồm nhiều biến liên quan chặt chẽ. Điều này giúp tiết kiệm thời gian, nâng cao tính khả thi của các phân tích tiếp theo như mô hình dự báo, phân tích cấu trúc hay mô hình đa biến phức tạp hơn.
Khác với các phương pháp khác, nguyên lý của EFA tập trung vào việc khám phá ra các yếu tố tiềm ẩn chứ không cần đặt trước các giả thuyết hay giả định về cấu trúc của dữ liệu. Chính vì vậy, phương pháp này rất phù hợp để sử dụng trong những nghiên cứu sơ bộ, khi chưa rõ cấu trúc nội tại của tập dữ liệu, hoặc khi muốn kiểm tra tính phù hợp của mô hình đo lường đang có.
Phân biệt EFA với các phương pháp khác
Trong hệ thống phân tích dữ liệu đa biến, phương pháp EFA thường bị nhầm lẫn hoặc so sánh nhiều với các kỹ thuật khác như CFA (Phân tích xác nhận) hay hồi quy tuyến tính. Điều quan trọng là hiểu rõ những điểm khác biệt cơ bản để chọn đúng phương pháp phù hợp với mục tiêu nghiên cứu.
Trong khi EFA tập trung vào việc khám phá cấu trúc tiềm ẩn của dữ liệu, thì CFA lại là phương pháp xác nhận, kiểm tra xem cấu trúc đã được thiết lập có phù hợp với dữ liệu hay không. CFA thường yêu cầu kích thước mẫu lớn hơn, giả định rõ ràng về số lượng nhân tố, các biến liên quan, giúp kiểm định tính hợp lệ của mô hình dựa trên lý thuyết đã có. Trong khi đó, EFA khá linh hoạt, không yêu cầu giả định trước về cấu trúc, phù hợp cho bước khám phá sơ bộ.
So sánh với phân tích hồi quy, EFA không đặt nặng việc dự đoán hoặc xác định mối quan hệ nhân quả giữa các biến. Thay vào đó, nó giúp xác định cấu trúc nội tại, các nhân tố tiềm ẩn, giúp định hướng cho các phân tích sâu hơn sau này. Do đó, khi muốn biết efa là gì đúng nghĩa, ta có thể hình dung như một dụng cụ khám phá cấu trúc nội tại của dữ liệu, còn các phương pháp khác lại phù hợp hơn trong quá trình kiểm định và dự báo.
Chọn lựa phương pháp phù hợp sẽ dựa vào mục đích và độ chi tiết của nghiên cứu, nhưng rõ ràng, EFA chính là bước tiền đề quan trọng để các phân tích phức tạp sau này được thực hiện chính xác và hiệu quả hơn.
Lợi ích của EFA trong nghiên cứu
Không thể phủ nhận, EFA mang lại nhiều lợi ích thiết thực trong quá trình phân tích dữ liệu nghiên cứu, giúp các nhà khoa học có cái nhìn toàn diện, chính xác hơn về cấu trúc nội tại của tập hợp biến đo lường. Một trong những điểm mạnh nổi bật chính là khả năng giảm số lượng biến đo lường một cách hiệu quả, giữ lại những yếu tố quan trọng nhất, và loại bỏ các biến dư thừa, không mang nhiều ý nghĩa.
Thứ hai, EFA giúp các nhà nghiên cứu hiểu rõ hơn về cấu trúc nội tại của dữ liệu. Khi phát hiện ra các nhân tố chính, ta có thể hiểu sâu hơn về các khái niệm và mối liên hệ giữa chúng, từ đó xây dựng các giả thuyết mới, thiết kế các mô hình phù hợp hơn. Khả năng này đặc biệt hữu ích trong các nghiên cứu về tâm lý hay xã hội, nơi mà các khái niệm thường rất phức tạp, trừu tượng.
Ngoài ra, phân tích nhân tố khám phá còn giúp chuẩn bị dữ liệu cho các phân tích phức tạp hơn như CFA, SEM hay các mô hình dự báo. Các nhân tố được rút ra có thể là các biến mới, đơn giản hóa quá trình phân tích, đồng thời tối ưu hóa độ chính xác của các mô hình dựa trên dữ liệu thực tế. Tóm lại, EFA không chỉ là công cụ phân tích, mà còn là bước đệm giúp nâng cao chất lượng nghiên cứu, gia tăng khả năng hiểu biết toàn diện, chính xác về nội dung và cấu trúc dữ liệu.
Các điều kiện và tiêu chí đánh giá khi áp dụng EFA trong SPSS
Điều kiện về mối quan hệ giữa các biến đo lường
Một yếu tố quyết định đến thành công của EFA chính là mức độ tương quan giữa các biến đo lường. Thông thường, các nhà phân tích sẽ dựa vào ma trận hệ số tương quan để đánh giá liệu tập hợp biến này có phù hợp để tiến hành phân tích nhân tố hay không. Nếu các hệ số tương quan nhỏ hơn 0.30, khả năng cao là dữ liệu không phù hợp, dẫn đến kết quả kết luận thiếu chính xác và gây ra nhiều mắc phải khi phân tích.
Trong quá trình kiểm tra, việc xác định mức độ quan hệ giữa các biến là bước then chốt để tránh rủi ro phân tích sai lệch hoặc không hợp lý. Các mối quan hệ này phản ánh mức độ liên hệ nội tại giữa các biến, từ đó giúp xác định xem tập dữ liệu có khả năng tạo ra các nhân tố nội tại phù hợp hay không. Nếu mức độ tương quan quá yếu, các nhân tố tiềm ẩn sẽ không rõ ràng, không đáng tin cậy để dùng trong mô hình phân tích sâu hơn.
Điều này đòi hỏi nhà phân tích phải kiểm tra ma trận hệ số tương quan trước khi tiến hành EFA, nhằm đảm bảo rằng các biến đều có liên hệ biểu hiện rõ ràng và phù hợp để khám phá nhân tố. Điều này không chỉ giúp đảm bảo tính hợp lệ của quá trình phân tích mà còn giảm thiểu rủi ro về mặt phân tích sai lệch, nâng cao chất lượng kết quả cuối cùng.
Kiểm định Bartlett và ý nghĩa của chúng trong EFA
Không thể nhầm lẫn, kiểm định Bartlett là một trong những bước kiểm tra quan trọng để đảm bảo điều kiện dữ liệu phù hợp cho phân tích nhân tố. Nhiệm vụ của kiểm định này là kiểm tra xem ma trận tương quan có phải là ma trận đơn vị hay không, điều đó có nghĩa là các biến đo lường không liên hệ chặt chẽ với nhau hoặc tạo ra các cấu trúc nội tại rõ ràng.
Kết quả kiểm định Bartlett có ý nghĩa thống kê đặc biệt trong việc xác định tính phù hợp của dữ liệu cho EFA. Nếu giá trị p = 0.05, khả năng lớn là dữ liệu không thích hợp để phân tích nhân tố, hoặc nội dung các biến chưa phản ánh đúng cấu trúc thực tế.
Chính vì vậy, việc thực hiện kiểm định Bartlett là bước bắt buộc để đảm bảo rằng dữ liệu của bạn đã sẵn sàng và phù hợp cho phân tích EFA, giúp tránh rủi ro phân tích sai lệch và đồng thời nâng cao độ tin cậy của kết quả cuối cùng.
Kiểm định KMO –Thước Đo Độ Phù Hợp Của Dữ Liệu Trước Khi Phân Tích Nhân Tố (EFA)
Trong phân tích nhân tố khám phá (EFA), kiểm định KMO (Kaiser – Meyer – Olkin) là bước đầu tiên và cực kỳ quan trọng để đánh giá xem dữ liệu có phù hợp để phân tích hay không.
KMO là chỉ số dùng để so sánh giữa hệ số tương quan đơn giản (giữa hai biến) và hệ số tương quan riêng phần (sau khi loại bỏ ảnh hưởng của các biến khác).
Nói đơn giản: KMO giúp xác định các biến có thực sự liên quan chặt chẽ với nhau để tạo thành các nhân tố hay không.
Cách Đọc Chỉ Số KMO
|
Giá trị KMO |
Đánh giá mức độ phù hợp |
|
KMO ≥ 0.90 |
Rất tốt |
|
0.80 ≤ KMO < 0.90 |
Tốt |
|
0.70 ≤ KMO < 0.80 |
Khá |
|
0.60 ≤ KMO < 0.70 |
Tạm được |
|
0.50 ≤ KMO < 0.60 |
Yếu – Cân nhắc sử dụng |
|
KMO < 0.50 |
❌ Không chấp nhận được |
📌 Lưu ý: Để thực hiện EFA, KMO phải ≥ 0.50 trở lên (theo đề xuất của Kaiser, 1974). Dưới mức này, dữ liệu được xem là không đủ điều kiện để tiến hành phân tích nhân tố.
Ý Nghĩa Thực Tiễn
- KMO cao (≥ 0.80) → Dữ liệu có cấu trúc rõ ràng, các biến quan sát liên quan tốt → Phân tích nhân tố sẽ cho ra kết quả tin cậy và ổn định
- KMO thấp (< 0.50) → Các biến đo lường liên hệ yếu hoặc rời rạc, không đủ điều kiện để trích xuất nhân tố → Nên xem lại dữ liệu, loại bỏ biến yếu hoặc làm sạch trước khi tiếp tục.
Tiêu chuẩn về kích thước mẫu phù hợp
Kích thước mẫu đóng vai trò then chốt đối với độ chính xác và tính khả thi của EFA. Một tập dữ liệu quá nhỏ sẽ dẫn đến kết quả thiếu ổn định, không đại diện đúng cho tổng thể, còn dữ liệu lớn hơn sẽ giúp phân tích chính xác hơn, tin cậy hơn. Thường thì, nguyên tắc chung đề cập đến việc kích thước mẫu nên gấp ít nhất 4 đến 5 lần số biến đo lường để đảm bảo chất lượng phân tích.
Các chuyên gia nghiên cứu đã đề nghị, để đạt chuẩn phù hợp với EFA, kích thước mẫu tối thiểu thường khoảng từ 50 đến 100 mẫu. Nếu số lượng biến đo lường lớn, càng cần kích thước mẫu lớn hơn, nhằm giảm thiểu rủi ro nhiễu loạn, mất ổn định của các nhân tố.
Thực tế, việc kiểm tra kích thước mẫu trước khi thực hiện phân tích không chỉ giúp đảm bảo các tiêu chí kỹ thuật, mà còn nâng cao tính khả thi của nghiên cứu. Lựa chọn đủ lớn mẫu không những đảm bảo kết quả phân tích chính xác mà còn phản ánh đúng cấu trúc nội tại của dữ liệu giúp các nhà nghiên cứu tự tin hơn khi kết luận và đưa ra các giả thuyết.
Hướng dẫn chạy EFA trong SPSS
Chuẩn bị dữ liệu cho phân tích EFA
Trước khi bắt đầu bất kỳ phân tích nào trong SPSS, điều quan trọng nhất chính là chuẩn bị dữ liệu một cách cẩn thận và kỹ lưỡng. Việc kiểm tra, xử lý dữ liệu trước khi chạy EFA giúp đảm bảo kết quả chính xác và giảm thiểu rủi ro mắc các lỗi gây nhiễu loạn dữ liệu. Đầu tiên, loại bỏ các biến không phù hợp hoặc các biến đã xác định rõ không liên quan đến mục tiêu nghiên cứu để tránh làm nhiễu kết quả.
Tiếp theo, việc kiểm tra tính độ tin cậy của các thang đo thông qua Cronbach Alpha là cần thiết để đảm bảo rằng các biến nằm trong cùng một khái niệm hoặc cấu trúc đo lường. Nếu các kết quả này cho thấy độ tin cậy thấp, các biến liên quan cần được xem xét loại bỏ hoặc chỉnh sửa để nâng cao chất lượng dữ liệu. Data cleansing còn bao gồm kiểm tra các điểm ngoại lệ, dữ liệu thiếu hoặc dữ liệu trùng lặp, đảm bảo tính nhất quán của bộ dữ liệu.
Trong quá trình chuẩn bị, cần tổ chức dữ liệu theo dạng phù hợp với yêu cầu của SPSS, đảm bảo không có lỗi định dạng hoặc dữ liệu không hợp lệ. Nhờ đó, các bước chạy EFA sẽ diễn ra suôn sẻ, chính xác hơn và kết quả cuối cùng phản ánh đúng nội dung thực tế của nghiên cứu.
Thực hiện phân tích EFA trong SPSS
Sau khi hoàn tất bước đánh giá độ tin cậy bằng Cronbach Alpha và loại bỏ các biến quan sát không đạt yêu cầu, bạn sẽ tiến hành phân tích nhân tố khám phá (EFA) để xác định cấu trúc các nhân tố tiềm ẩn. Lưu ý: Chỉ đưa vào EFA những biến quan sát còn lại sau Cronbach Alpha.
💡 Thực hiện EFA riêng biệt cho nhóm biến độc lập và biến phụ thuộc để đảm bảo cấu trúc nhân tố rõ ràng và chính xác.
Các Bước Thực Hiện EFA Trong SPSS 20
Bước 1: Truy cập tính năng phân tích
- Vào Analyze > Dimension Reduction > Factor…
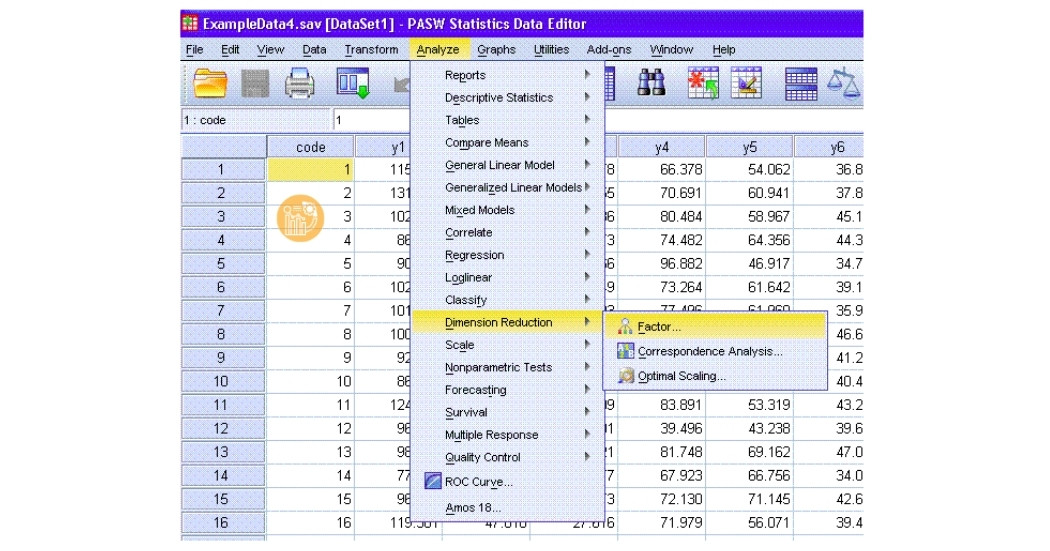
Bước 2: Chọn biến phân tích
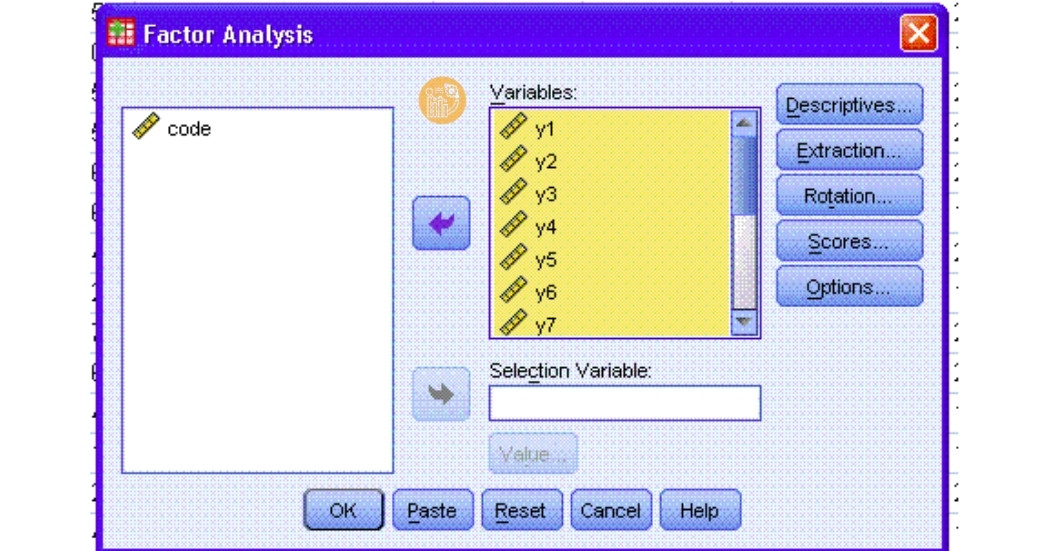
- Trong hộp thoại hiện ra, đưa các biến quan sát cần phân tích EFA vào ô Variables.
- Chỉ chọn các biến đạt Cronbach Alpha, không đưa biến đã bị loại ở bước trước vào.
Thiết Lập Các Tùy Chọn Phân Tích
1. Descriptives
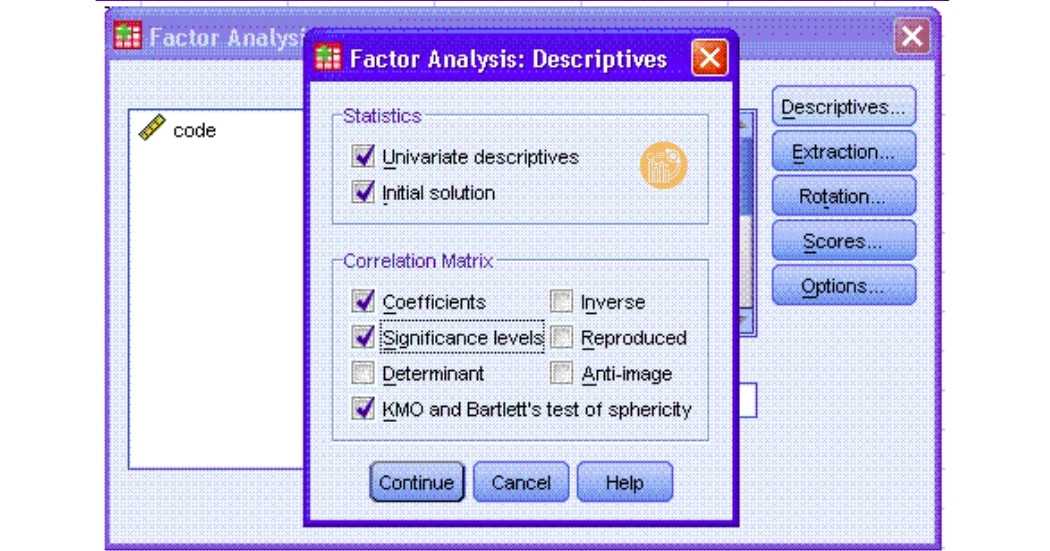
- Nhấp vào Descriptives → tích chọn:
- KMO and Bartlett’s test of sphericity
- Nhấn Continue để quay lại.
2. Extraction
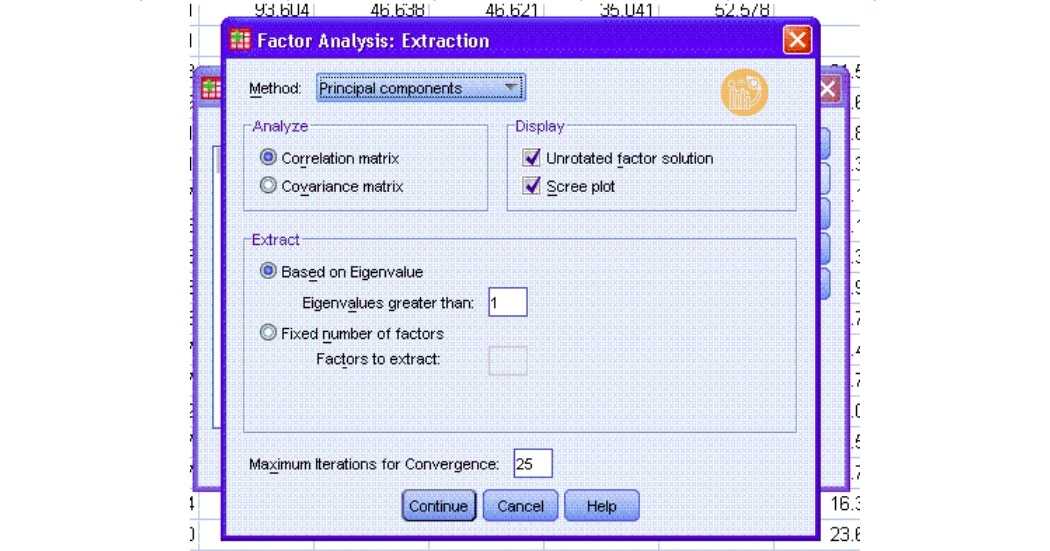
- Trong mục Extraction:
- Chọn phương pháp trích: Principal Components (mặc định).
- Tích chọn Eigenvalues greater than 1 (chỉ trích các nhân tố có giá trị riêng > 1).
- Ghi chú: SPSS 20 trở đi hiển thị phương pháp này dưới tên Principal Components (viết gọn từ PCA).
- Nhấn Continue để quay lại.
3. Rotation
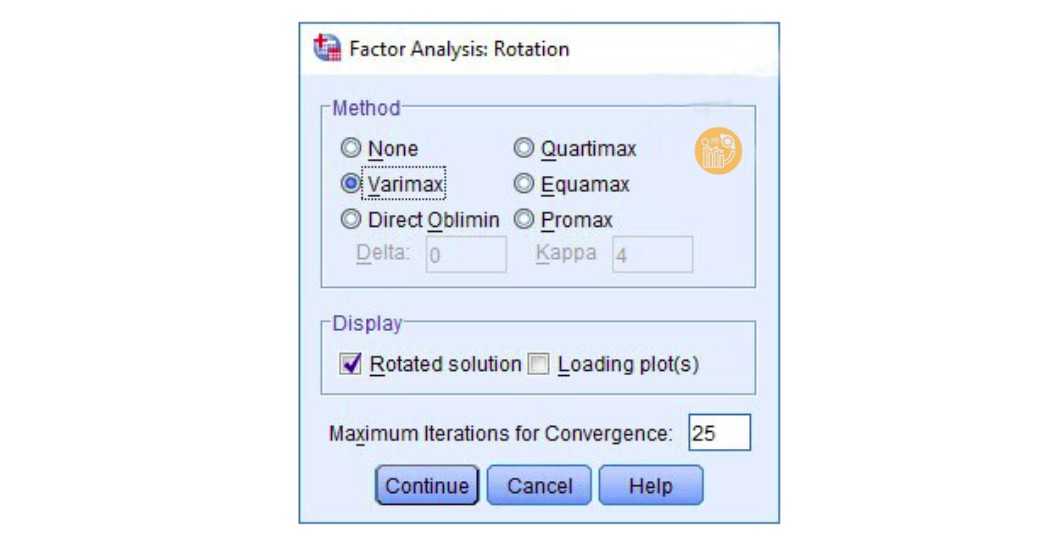
- Trong phần Rotation:
- Chọn phương pháp Varimax (trường hợp bạn phân tích riêng biến độc lập/phụ thuộc).
- Promax dùng trong một số trường hợp biến có khả năng liên quan nhau.
- Nhấn Continue để quay lại.
4. Options
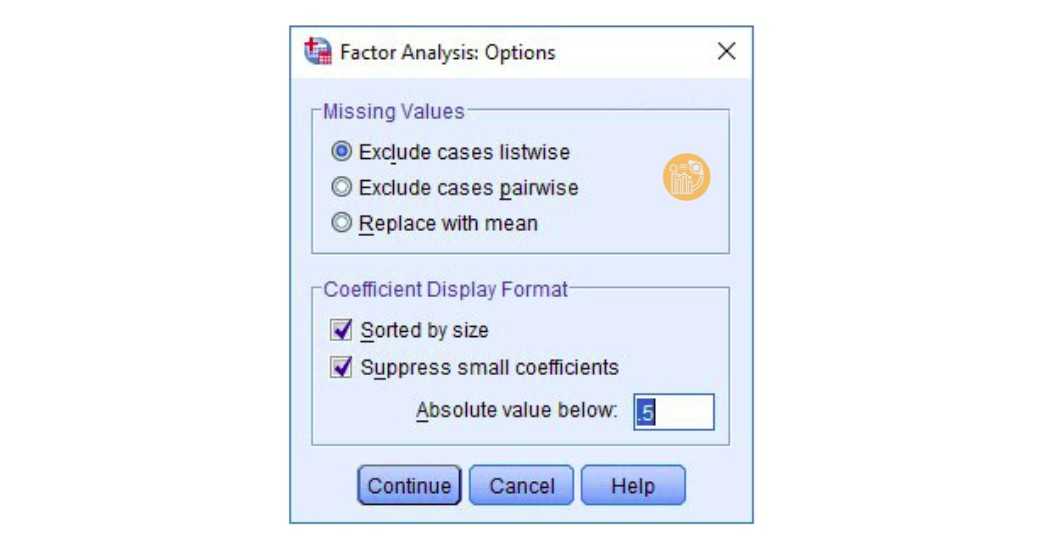
- Tích vào 2 mục sau:
- Sorted by size → giúp sắp xếp các hệ số tải trong ma trận xoay.
- Suppress small coefficients → loại bỏ các hệ số tải nhỏ.
- Tại ô Absolute value below, nhập giá trị hệ số tải tối thiểu (thường dùng 0.5 nếu cỡ mẫu từ 200 trở lên, như ví dụ này là n = 220).
- Nhấn Continue để quay lại.
Thực thi phân tích
- Nhấn OK để SPSS chạy phân tích và xuất kết quả ra cửa sổ Output.
Diễn Giải Kết Quả – Chỉ Quan Tâm 3 Bảng Chính
| Tên bảng | Mục đích |
|---|---|
| KMO and Bartlett’s Test | Kiểm tra điều kiện dữ liệu có phù hợp để phân tích EFA không (KMO ≥ 0.5) |
| Total Variance Explained | Xem số lượng nhân tố trích được và tổng phương sai trích (%) |
| Rotated Component Matrix | Ma trận xoay – xem hệ số tải của từng biến vào từng nhân tố cụ thể |
🧠 Ghi nhớ:

- Chỉ số KMO ≥ 0.5 → Dữ liệu phù hợp để phân tích EFA.
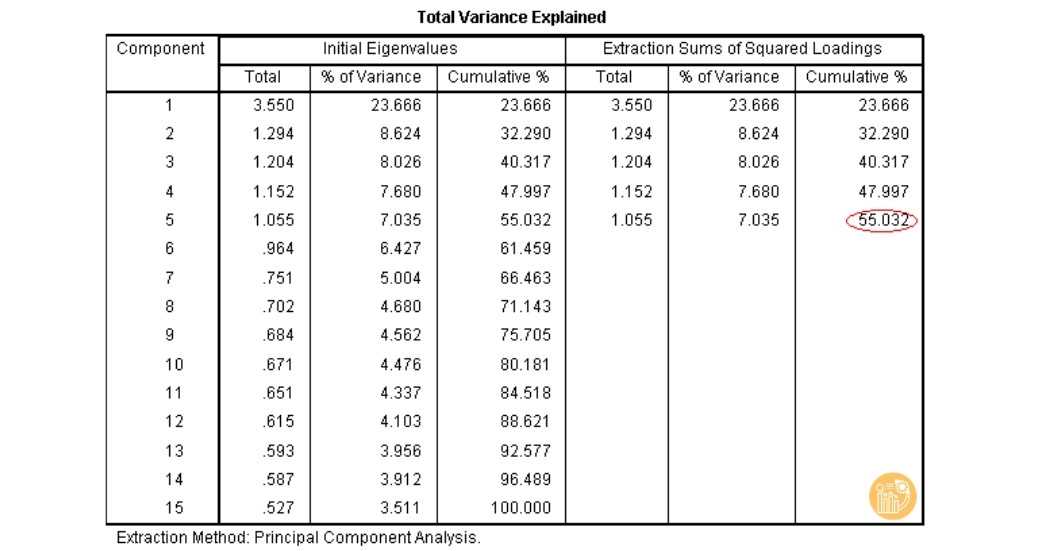
- Phương sai trích ≥ 50% → Dữ liệu giải thích tốt các nhân tố.
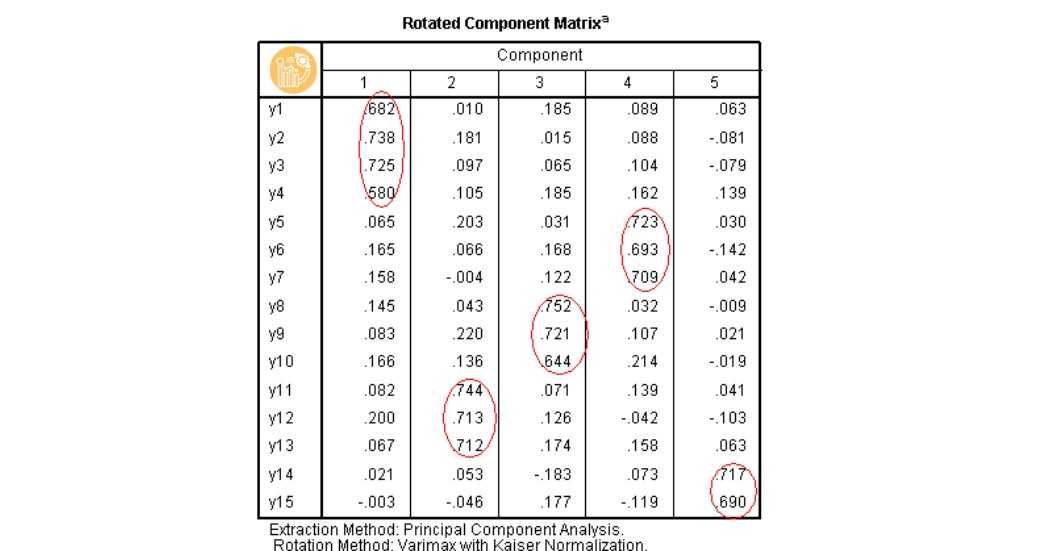
- Hệ số tải ≥ 0.5 → Biến quan sát được xem là có ý nghĩa đại diện cho nhân tố.
Diễn giả và phân tích kết quả EFA
Chìa khóa thành công của EFA chính là khả năng hiểu và phân tích các kết quả một cách thấu đáo. Khi kết thúc quá trình trong SPSS, bảng KMO và kiểm định Bartlett sẽ giúp bạn xác nhận rằng dữ liệu đủ điều kiện để tiếp tục phân tích. Tiếp theo, bảng Total Variance Explained cho thấy phần trăm biến đổi do các nhân tố chính mang lại, giúp xác định số lượng nhân tố cần giữ lại.
Ma trận xoay Rotated Component Matrix là phần quan trọng nhất để xác định các yếu tố rõ ràng. Trong bảng này, các biến có hệ số tải (loading factor) lớn hơn ngưỡng quy định (thường là 0.5 hoặc 0.6) sẽ được xem là liên quan chặt chẽ đến nhân tố đó. Thông qua việc phân tích cẩn thận, nhà nghiên cứu có thể xác định được các nhóm biến phù hợp với từng nhân tố, từ đó đặt tên, mô tả nội dung của từng yếu tố một cách rõ ràng và thông minh hơn.
Hãy nhớ rằng, kết quả EFA không chỉ để thể hiện ý nghĩa thống kê, mà còn phản ánh chính xác nội dung khoa học của đề tài. Việc diễn giải khéo léo, dựa trên nội dung các biến, giúp hình thành các khái niệm, mô hình rõ ràng, phù hợp với lý thuyết và thực tiễn nghiên cứu. Đồng thời, bạn cần lưu ý các điểm ngoại lệ, các biến có hệ số tải thấp để có quyết định điều chỉnh phù hợp nhằm nâng cao độ tin cậy của mô hình.
Kết luận
Phân tích nhân tố khám phá (EFA) không chỉ là một phương pháp phân tích dữ liệu mạnh mẽ mà còn là công cụ giúp các nhà nghiên cứu nắm bắt, rút gọn và hiểu rõ các cấu trúc nội tại của tập hợp biến đo lường. Qua quá trình tìm hiểu về khái niệm, nguyên lý hoạt động, các điều kiện áp dụng cùng cách thực hiện chi tiết trong SPSS, chúng ta nhận thấy rằng EFA là bước quan trọng để chuẩn bị dữ liệu cho các phân tích sâu hơn trong nghiên cứu khoa học. Với việc biết rõ các tiêu chuẩn, điều kiện và cách vận dụng đúng quy trình, các nhà nghiên cứu sẽ dễ dàng, chính xác hơn trong việc khám phá ra các nhân tố tiềm ẩn, từ đó nâng cao tính khách quan, khoa học của nghiên cứu. Tổng thể, EFA chính là chìa khóa mở ra những kiến thức mới mẻ, toàn diện và chính xác về cấu trúc dữ liệu, góp phần quan trọng vào thành công của các đề tài nghiên cứu cũng như các ứng dụng thực tiễn trong đời sống.















