Mục lục
TogglePhương Pháp Hồi Quy Tuyến Tính là gì?
Trong thế giới khoa học dữ liệu và trí tuệ nhân tạo, phương trình hồi quy tuyến tính là một trong những công cụ cổ điển nhưng vô cùng mạnh mẽ để phân tích mối liên hệ giữa các biến số. Phương pháp này không chỉ đơn giản trong cách thực hiện, mà còn có khả năng cung cấp những dự báo chính xác đối với các hiện tượng tuyến tính diễn ra trong tự nhiên hoặc trong các hệ thống kỹ thuật phức tạp như hồ thủy điện.
Định nghĩa và ý nghĩa
Hồi quy tuyến tính là một phương pháp trong thống kê, giúp xác định mối quan hệ tuyến tính giữa một biến phụ thuộc (biến mục tiêu) và một hoặc nhiều biến độc lập (biến dự đoán). Trong hình thức đơn giản nhất, với một biến độc lập, hàm hồi quy sẽ có dạng y = ax + b, với a và b là các hệ số cần xác định để mô tả tốt nhất mối liên hệ này.
Ý nghĩa của phương pháp này nằm ở khả năng dự đoán nhanh chóng và dễ hiểu dựa trên mô hình tuyến tính đã xây dựng. Trong các lĩnh vực như kinh tế, khí tượng, kỹ thuật, hay quản lý tài nguyên thiên nhiên, việc áp dụng hồi quy tuyến tính giúp đưa ra các quyết định dựa trên dữ liệu thực tế, đồng thời giúp nhận diện các yếu tố ảnh hưởng quan trọng tới biến mục tiêu.
Ứng dụng trong các lĩnh vực
Không dừng lại ở lĩnh vực quản lý tài nguyên, phương pháp hồi quy tuyến tính còn được ứng dụng rộng rãi trong phân tích thị trường tài chính, dự báo doanh số, kiểm soát chất lượng sản phẩm, hay dự đoán khí tượng thủy văn. Chẳng hạn, trong ngành thủy lợi, mô hình này giúp xác định mối liên hệ giữa lượng mưa và lượng nước xả lũ, từ đó đưa ra các giải pháp vận hành phù hợp.
Trong lĩnh vực khí tượng, các nhà nghiên cứu sử dụng hồi quy tuyến tính để dự báo nhiệt độ, lượng mưa dựa trên các yếu tố khí tượng như độ ẩm, áp suất không khí. Còn trong quản lý rủi ro thiên tai, phương pháp này giúp xác định mức độ ảnh hưởng của các yếu tố môi trường tới các hiện tượng cực đoan như lũ lụt, hạn hán.
Vai trò trong dự báo xả lũ thủy điện
Trong quá trình vận hành nhà máy thủy điện, việc dự báo chính xác lượng xả lũ dựa trên mực nước hồ là yếu tố then chốt để đảm bảo an toàn cho con người và hệ sinh thái. Phương trình hồi quy tuyến tính mang lại công cụ dự báo nhanh chóng, phù hợp với các dữ liệu rời rạc, khả năng mô phỏng các mối quan hệ phức tạp trong tự nhiên.
Với khả năng phân tích các dữ liệu thực tế về mực nước và dòng chảy, mô hình này giúp các kỹ sư và nhà quản lý dự đoán chính xác lượng nước cần xả để duy trì độ an toàn của hồ, tránh các sự cố đột xuất. Từ đó, giúp tối ưu hóa quá trình vận hành, giảm thiểu thiệt hại về tài chính và môi trường.
Ứng Dụng Phương Trình Hồi Quy Tuyến Tính Trong Dự Báo Lượng Nước Xả Lũ

Mô Tả Bài Toán
Khi mực nước trong hồ thủy điện dâng cao do nước lũ, việc xả lũ là cần thiết để đảm bảo an toàn cho công trình. Để thực hiện việc xả lũ một cách hợp lý, cần có một phương pháp dự báo chính xác lượng nước cần xả. Một trong các cách tiếp cận hiệu quả là sử dụng phương trình hồi quy tuyến tính nhằm mô hình hóa mối quan hệ giữa mực nước trong hồ và lưu lượng xả.
Nhóm nghiên cứu đã lựa chọn phương pháp này để xây dựng một mô hình dự báo đơn giản nhưng hiệu quả, dựa trên dữ liệu thu thập từ thực tế. Phương trình hồi quy tuyến tính có dạng:
f(x) = ax + b
Trong đó:
xlà mực nước trong hồ.f(x)là lượng nước cần xả.avàblà các hệ số hồi quy được xác định từ dữ liệu.
Giải Pháp Liên Quan
Ngoài phương trình hồi quy tuyến tính, có nhiều thuật toán khác đã được sử dụng trong bài toán tối ưu lượng nước xả như:
- Phương pháp hồi quy tuyến tính
- Thuật toán di truyền (Genetic Algorithm – GA),
- Tối ưu hóa đàn kiến (Ant Colony Optimization – ACO),
- Tối ưu bầy đàn (Particle Swarm Optimization – PSO),
- Tối ưu bầy mèo (Cat Swarm Optimization – CSO).
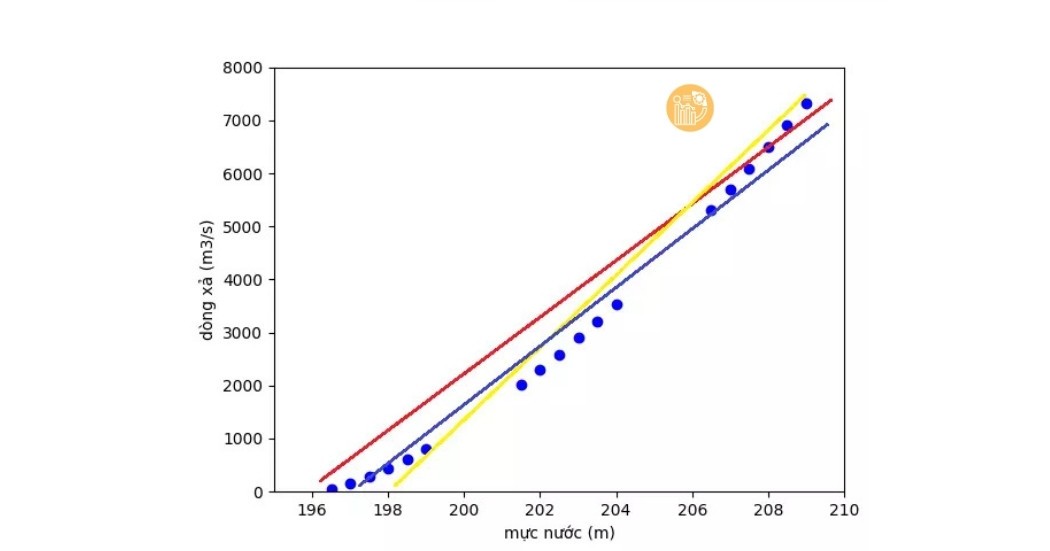
Các thuật toán này chủ yếu tìm bộ tham số hồi quy w = [α, β] bằng cách tìm kiếm ngẫu nhiên và cập nhật qua các thế hệ để tiệm cận nghiệm tối ưu. Tuy nhiên, chúng phụ thuộc vào điều kiện khởi tạo ban đầu. Trong khi đó, phương trình hồi quy tuyến tính giúp ta tìm nghiệm chính xác hơn trong trường hợp dữ liệu tuyến tính và rời rạc.
Mô Hình Phương Trình Hồi Quy Tuyến Tính
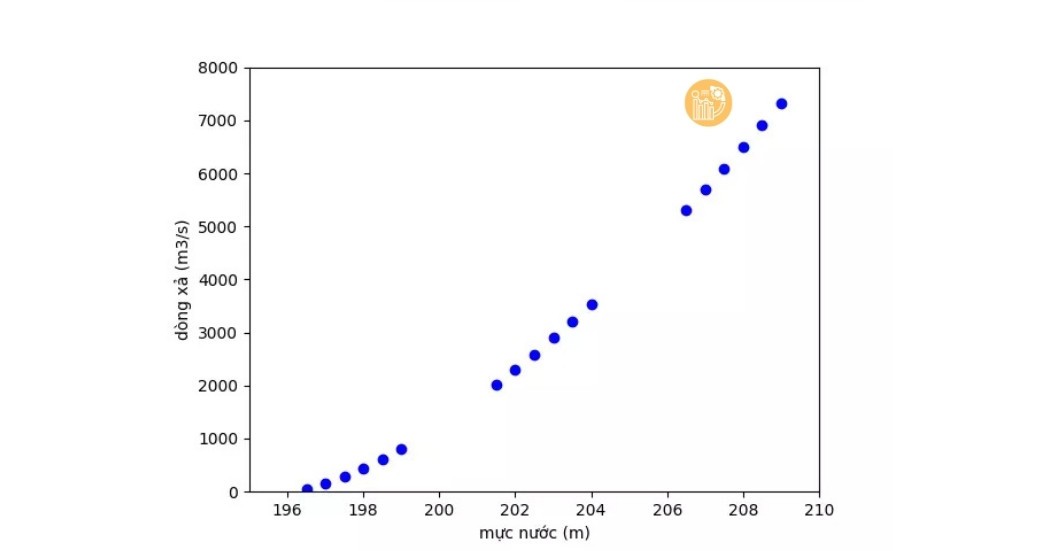
Mô tả các điểm dữ liệu
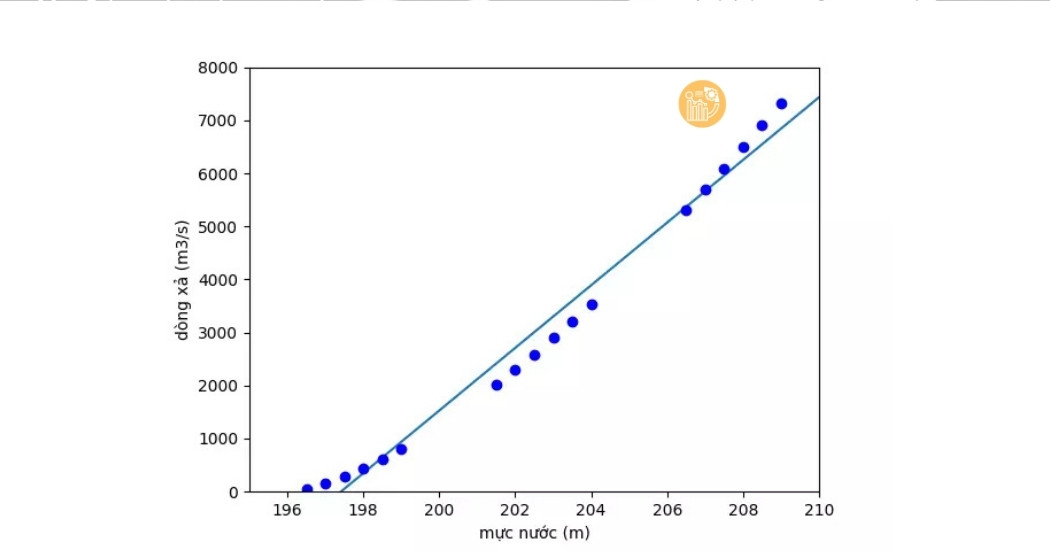
Cho tập dữ liệu các điểm (xi, yi) trên mặt phẳng tọa độ. Bài toán đặt ra là tìm hàm số y = ax + b sao cho sai số giữa các điểm dữ liệu và đường hồi quy là nhỏ nhất.
Biểu diễn bằng hệ phương trình:
y0 = a*x0 + b
y1 = a*x1 + b
...
yn = a*xn + b
Ta có thể viết lại dưới dạng ma trận:
Y = a * X + b * C
Trong đó:
Y = [y0, y1, ..., yn]^TX = [x0, x1, ..., xn]^TC = [1, 1, ..., 1]^T
Ta cần tìm vector w = [a, b] sao cho:
w = (V^T * V)^(-1) * V^T * Y
Trong đó:
Vlà ma trận ghép từXvàC.
Phương trình trên chính là công thức hồi quy tuyến tính chuẩn dựa trên giải tích ma trận.
Ứng Dụng Dữ Liệu Thực Tế
Dữ liệu đầu vào
Ta cùng xem xét bảng dữ liệu:
| Mực nước (m) | Lưu lượng xả (m³/s) |
|---|---|
| 196.5 | 55 |
| 197.0 | 156 |
| 197.5 | 287 |
| 198.0 | 442 |
| 198.5 | 618 |
| 199.0 | 812 |
| 201.5 | 2016 |
| 202.0 | 2297 |
| 202.5 | 2590 |
| 203.0 | 2894 |
| 203.5 | 3210 |
| 204.0 | 3536 |
| 206.5 | 5317 |
| 207.0 | 5701 |
| 207.5 | 6094 |
| 208.0 | 6496 |
| 208.5 | 6906 |
| 209.0 | 7325 |
Cài đặt trong Python
import numpy as np
import matplotlib.pyplot as plt
# Dữ liệu
dong_xa_oy = np.array([[55, 156, 287, 442, 618, 812, 2016, 2297, 2590,
2894, 3210, 3536, 5317, 5701, 6094, 6496,
6906, 7325]]).T
muc_nuoc_ox = np.array([[196.5, 197., 197.5, 198., 198.5, 199.,
201.5, 202., 202.5, 203., 203.5, 204.,
206.5, 207., 207.5, 208., 208.5, 209.0]]).T
# Biểu đồ
plt.xlabel('Mực nước (m)')
plt.ylabel('Dòng xả (m³/s)')
plt.plot(muc_nuoc_ox, dong_xa_oy, 'bo')
plt.show()
Hàm tính nghiệm hồi quy
def linear_regression(y_vector, v_matrix):
w_1 = np.linalg.pinv(np.dot(v_matrix.T, v_matrix))
w_2 = np.dot(v_matrix.T, y_vector)
w = np.dot(w_1, w_2)
return w
b_vector = np.ones((muc_nuoc_ox.shape[0], 1))
a_matrix = np.concatenate((b_vector, muc_nuoc_ox), axis=1)
# Tính nghiệm
liner_vector = linear_regression(dong_xa_oy, a_matrix)
print("Nghiệm w tính bằng tay:", liner_vector.T)
So sánh với sklearn
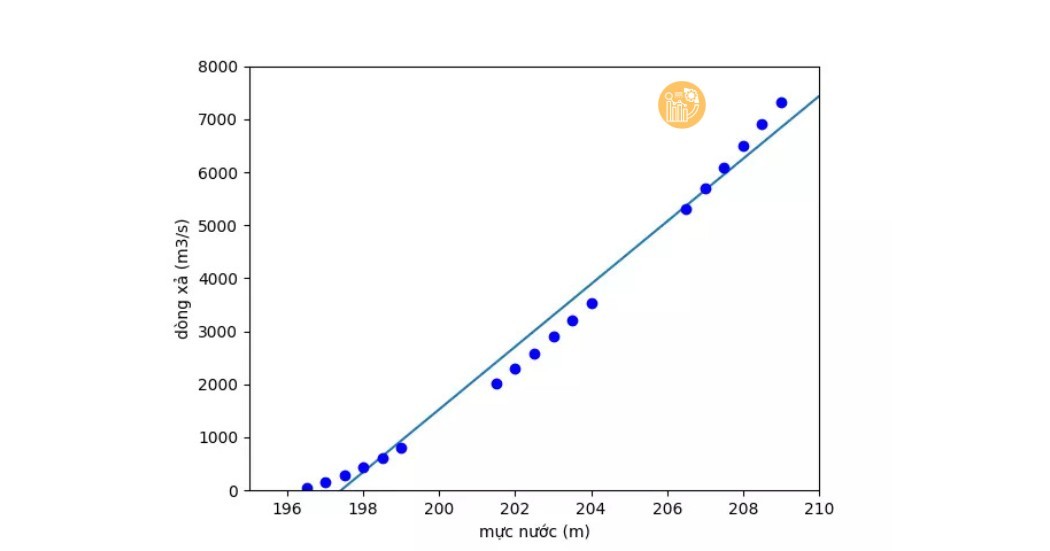
Kết quả của XULYSOLIEU
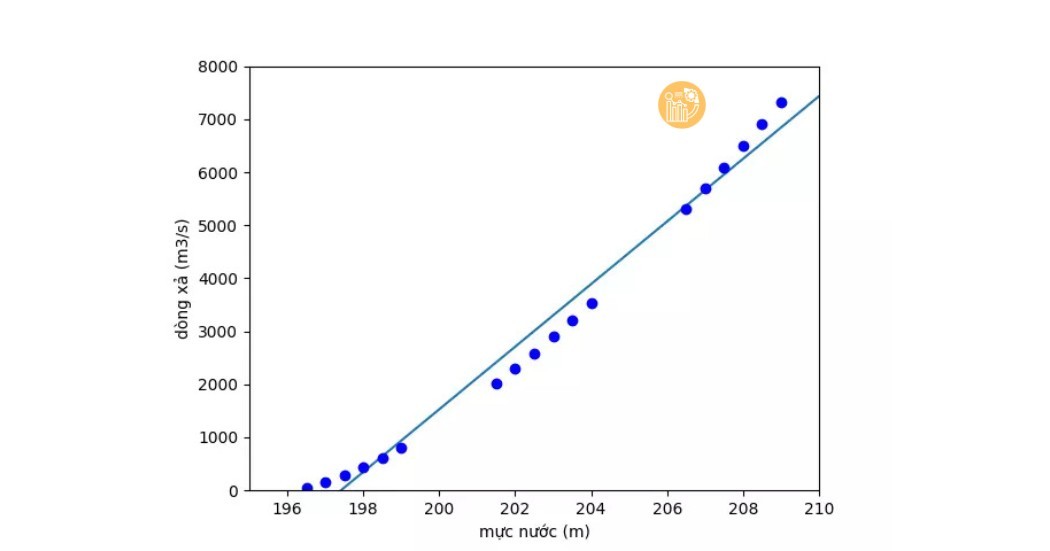
Kết quả của sklearn model
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False)
model.fit(a_matrix, dong_xa_oy)
print("Nghiệm w bằng sklearn:", model.coef_)
Kết quả:
Solution found by sklearn: w = [[-116539.37977378 590.34411178]]
Solution found by me: w = [[-116539.37979331 590.34411187]]
Hai kết quả tương đương → xác nhận tính đúng đắn của phương trình hồi quy tuyến tính.
Dự báo giá trị mới
a = liner_vector[1][0]
b = liner_vector[0][0]
x_test = np.array([200, 205])
y_predict = a * x_test + b
print(f"Mực nước 200m → xả khoảng: {round(y_predict[0], 2)} m³/s")
print(f"Mực nước 205m → xả khoảng: {round(y_predict[1], 2)} m³/s")
Kết quả:
Mực nước 200m → xả khoảng: 1529.44 m³/s
Mực nước 205m → xả khoảng: 4481.16 m³/s
Công Thức Toán Học của Phương Pháp Hồi Quy Tuyến Tính

Đi sâu vào lý thuyết toán học, phương trình hồi quy tuyến tính dựa trên các phép biến đổi ma trận và vector, giúp xác định hệ số a, b một cách chính xác nhất. Các phép tính này giúp ta dễ dàng thực hiện trên các phần mềm xử lý số liệu hoặc ngôn ngữ lập trình như Python, R, hay MATLAB.
Phân tích dữ liệu theo mặt phẳng Oxy
Trong dạng đơn giản, các điểm dữ liệu cần được phân tích trong mặt phẳng Oxy, với trục hoành là biến độc lập (x – mực nước hồ) và trục tung là biến phụ thuộc (y – lượng xả lũ). Hình ảnh mô tả trực quan các điểm dữ liệu này cho phép hình dung rõ ràng các mối liên hệ.
Trong hình không gian 3 chiều, các điểm dữ liệu không nằm cùng một mặt phẳng, dẫn đến việc cần tìm phẳng phù hợp nhất sao cho các điểm này được dự đoán gần đúng nhất. Chính quá trình này đòi hỏi tiến hành các phép tính toán để xác định hệ số phù hợp.
Hàm dự báo tuyến tính: y = ax + b
Phương trình này thể hiện mối liên hệ giữa đầu vào và đầu ra dưới dạng tuyến tính rõ ràng. Trong đó, a đại diện cho độ dốc của đường thẳng, cho biết mức độ ảnh hưởng của biến x đến y, còn b là hệ số điều chỉnh phản ánh giá trị của y khi x = 0. Công thức này phản ánh rõ ràng đặc điểm tuyến tính trong dữ liệu.
Biểu diễn dữ liệu dạng vector và ma trận
Để tối ưu hóa việc tính toán, ta biểu diễn dữ liệu thành các vector như y, x, và c (vector toàn phần gồm các phần tử bằng 1 để tính hệ số b). Các phương trình dữ liệu trở thành các biểu thức ma trận, mở ra khả năng ứng dụng các phép toán ma trận để tìm nghiệm tối ưu nhanh chóng.
Phương trình tối ưu để tìm hệ số a, b
Dựa trên nguyên lý bình phương nhỏ nhất, hệ số hồi quy w = [a, b] được tìm bằng công thức: w = (V^T V)^(-1) V^T y, trong đó V là ma trận dữ liệu đã được chuẩn hoá. Công thức này giúp xác định các hệ số phù hợp nhất để dự báo, dựa trên dữ liệu thực tế.
Áp dụng công thức vào bài toán cụ thể
Trong bài toán dự báo xả lũ thủy điện, ta sẽ lập ma trận V từ dữ liệu mực nước và hệ số b, sau đó tính toán để tìm ra các hệ số a, b sao cho mô hình hoạt động chính xác nhất, dựa trên dữ liệu lịch sử. Quá trình này giúp dự báo lượng xả tương lai, từ đó nâng cao hiệu quả quản lý hệ thống hồ chứa.
Ưu Điểm & Nhược Điểm của Phương Pháp Này
Dù rất phổ biến, phương trình hồi quy tuyến tính vẫn tồn tại những ưu nhược điểm rõ ràng cần xem xét cẩn thận trong từng ứng dụng.
Ưu điểm: đơn giản, dễ thực hiện, hiệu quả cao với dữ liệu tuyến tính
Các ưu điểm nổi bật của phương pháp này là tính đơn giản, dễ hiểu, dễ thực hiện và khả năng mô hình hóa nhanh chóng các hệ thống tuyến tính. Trong nhiều trường hợp, nó cung cấp các kết quả chính xác và đủ khả năng để dự báo trong phạm vi dữ liệu đã quan sát.
Bởi tính linh hoạt và ít yêu cầu về phần cứng, hồi quy tuyến tính phù hợp trong các hệ thống có dữ liệu ít phức tạp hoặc khi thời gian phân tích hạn chế. Ngoài ra, khả năng giải thích hệ số của mô hình còn giúp các nhà nghiên cứu, kỹ sư dễ dàng nhận diện các mối liên hệ trong dữ liệu.
Nhược điểm: nhạy cảm với dữ liệu nhiễu, hạn chế trong mô hình phức tạp
Tuy nhiên, phương pháp này rất nhạy cảm với các ngoại lệ, dữ liệu nhiễu hoặc các quan hệ phi tuyến tính mà không thể giải thích bằng mô hình tuyến tính. Trong các hệ thống phức tạp, mối quan hệ giữa các biến không thực sự tuyến tính, dẫn đến mô hình này không thể dự báo chính xác.
Ngoài ra, hồi quy tuyến tính không xử lý tốt các biến số bị đa cộng tuyến hoặc có mối liên hệ mạnh giữa chúng, gây ảnh hưởng tới độ ổn định của các hệ số mô hình. Để khắc phục, cần kết hợp các kỹ thuật tiền xử lý hoặc lựa chọn các mô hình phức tạp hơn như hồi quy phi tuyến.
Các hạn chế trong thực tế và cách khắc phục
Trong thực tế, điều kiện dữ liệu không lý tưởng sẽ khiến mô hình bị lệch, không chính xác. Để hạn chế những hạn chế này, có thể áp dụng các phương pháp bổ sung như regularization, dùng thuật toán PCA để giảm chiều dữ liệu hoặc chuyển sang các mô hình phi tuyến phù hợp hơn.
Điều này đặc biệt quan trọng trong ứng dụng khí tượng thủy văn, nơi biến đổi khí hậu gây ra các yếu tố phi tuyến và dữ liệu không ổn định. Tựu trung, sự kết hợp giữa hồi quy tuyến tính và các kỹ thuật nâng cao sẽ giúp mô hình trở nên linh hoạt và chính xác hơn trong các tình huống thực tế.
Kết Luận
Phương trình hồi quy tuyến tính là một công cụ căn bản nhưng cực kỳ hữu ích trong việc phân tích mối quan hệ giữa các biến số, đặc biệt trong lĩnh vực khí tượng thủy văn như dự báo lượng xả lũ hồ thủy điện. Tuỳ thuộc vào tính chất dữ liệu và yêu cầu mô hình, các nhà quản lý có thể lựa chọn phương pháp phù hợp, từ đơn giản như hồi quy tuyến tính đến phức tạp hơn như các thuật toán tối ưu hóa bầy đàn. Dù gặp hạn chế về tính phi tuyến và nhiễu dữ liệu, nhưng với các cải tiến kỹ thuật và kết hợp phù hợp, phương pháp này vẫn đóng vai trò chủ đạo trong các hệ thống dự báo hiệu quả, góp phần bảo vệ an toàn cộng đồng và tài nguyên.
Tài Liệu Tham Khảo
- Wikipedia – Linear Regression.
- Ths. Lê Xuân Cầu. Xây dựng biểu đồ vận hành khẩn cấp kiểm soát lũ. Viện KHKT Khí tượng Thủy văn & BĐKH, Tạp chí Khí tượng Thủy văn, 01/2015, tr.22–26















