SEM Model là gì? Tổng quan mô hình phương trình cấu trúc và cách áp dụng trong SPSS/AMOS
SEM Model (Structural Equation Modeling) là một trong những công cụ phân tích thống kê hiện đại và mạnh mẽ nhất hiện nay, đặc biệt phổ biến trong nghiên cứu khoa học xã hội, marketing, tâm lý học và kinh tế học. Bài viết này từ Xử lý số liệu sẽ giúp bạn hiểu rõ mô hình SEM là gì, nguyên lý hoạt động, cách phân tích SEM Model trong SPSS/AMOS và những ứng dụng thực tế trong nghiên cứu dữ liệu.
1. SEM Model là gì?
SEM Model hay mô hình phương trình cấu trúc là kỹ thuật phân tích thống kê dùng để kiểm định các mối quan hệ đa chiều giữa nhiều biến trong cùng một mô hình. Điểm khác biệt lớn nhất của SEM Model so với các phương pháp như hồi quy tuyến tính hay phân tích nhân tố là khả năng làm việc đồng thời với cả biến quan sát và biến tiềm ẩn.
Structural Equation Modeling cho phép nhà nghiên cứu mô tả và kiểm định các mối quan hệ nhân quả phức tạp, giúp xác định liệu mô hình lý thuyết có phù hợp với dữ liệu thực tế hay không. Đây là công cụ không thể thiếu trong phân tích mô hình SEM bằng phần mềm SPSS hoặc AMOS.
Hiểu đơn giản, SEM Model là sự kết hợp giữa hai phương pháp: phân tích nhân tố khẳng định (CFA) và hồi quy tuyến tính đa biến. Nhờ đó, mô hình có thể đánh giá cả chất lượng của thang đo và mối quan hệ giữa các khái niệm tiềm ẩn.
2. Lịch sử và sự phát triển của SEM Model
Structural Equation Modeling ra đời từ nhu cầu mở rộng khả năng phân tích dữ liệu vượt qua giới hạn của các kỹ thuật thế hệ đầu như hồi quy, ANOVA hay phân tích nhân tố. Sự phát triển của máy tính và các phần mềm thống kê như SPSS, AMOS, SmartPLS đã giúp SEM Model trở nên phổ biến và dễ sử dụng hơn bao giờ hết.
Ngày nay, các nghiên cứu học thuật và ứng dụng trong doanh nghiệp thường sử dụng SEM Model để mô tả hành vi con người, ví dụ như hành vi tiêu dùng, sự hài lòng khách hàng hay ý định mua hàng.
3. Ưu điểm nổi bật của SEM Model
So với các mô hình thống kê truyền thống, SEM Model mang lại nhiều lợi ích vượt trội:
- Kiểm định đồng thời nhiều giả thuyết nhân quả trong cùng một mô hình.
- Phân tích cả biến quan sát và biến tiềm ẩn.
- Đánh giá độ phù hợp tổng thể của mô hình với dữ liệu thực tế.
- Kết hợp giữa phân tích nhân tố và phân tích hồi quy.
- Ước lượng được độ tin cậy và giá trị khái niệm của thang đo.
- Cho phép điều chỉnh và cải thiện các mô hình chưa phù hợp.
Vì vậy, khi thực hiện phân tích mô hình SEM trong SPSS hoặc AMOS, người nghiên cứu có thể đồng thời kiểm định mô hình đo lường (measurement model) và mô hình cấu trúc (structural model), giúp đưa ra kết luận toàn diện hơn.
4. Thành phần cơ bản của SEM Model
4.1. Biến quan sát (Observed Variables)
Biến quan sát là những biến có thể đo lường trực tiếp thông qua bảng hỏi, dữ liệu khảo sát hay số liệu thực tế. Đây là dữ liệu thô được dùng để phản ánh các khái niệm tiềm ẩn. Ví dụ: các câu hỏi trong khảo sát về “mức độ hài lòng” là các biến quan sát.
4.2. Biến tiềm ẩn (Latent Variables)
Biến tiềm ẩn là khái niệm không thể đo lường trực tiếp, mà được suy ra thông qua các biến quan sát. Ví dụ: “sự hài lòng”, “niềm tin thương hiệu”, “động lực học tập”. Đây là điểm mạnh của SEM Model so với các mô hình thống kê truyền thống.
4.3. Biến trung gian (Mediator Variables)
Biến trung gian giúp xác định cách thức mà biến độc lập ảnh hưởng đến biến phụ thuộc. Trong Structural Equation Modeling, phân tích biến trung gian giúp hiểu sâu hơn về mối quan hệ gián tiếp giữa các khái niệm.
4.4. Biến chỉ báo phản ánh và cấu tạo
Biến chỉ báo phản ánh (Reflective Indicators) là biến thể hiện kết quả đo lường từ khái niệm tiềm ẩn. Trong khi đó, biến chỉ báo cấu tạo (Formative Indicators) là những yếu tố tạo nên khái niệm tiềm ẩn. Việc xác định loại biến này rất quan trọng trong quá trình xây dựng mô hình SEM.
5. Hai phần chính của SEM Model: CFA và Structural Model
SEM Model được chia thành hai phần lớn:
5.1. CFA (Confirmatory Factor Analysis)
Đây là bước đầu tiên trong phân tích mô hình SEM, dùng để kiểm định chất lượng thang đo. CFA giúp xác định xem các biến quan sát có phản ánh chính xác các biến tiềm ẩn hay không. Đây là lý do vì sao câu hỏi “CFA và SEM khác nhau thế nào” thường được đặt ra. CFA là một phần của SEM, tập trung vào mối quan hệ giữa các biến đo lường, trong khi SEM tổng hợp thêm các mối quan hệ nhân quả giữa các biến tiềm ẩn.
5.2. Mô hình cấu trúc (Structural Model)
Mô hình cấu trúc là phần chính của Structural Equation Modeling, mô tả các mối quan hệ nhân quả giữa các biến tiềm ẩn. Khi chạy AMOS SEM hướng dẫn, mô hình cấu trúc giúp bạn xác định hướng tác động giữa các biến, mức độ ảnh hưởng và giá trị thống kê kiểm định.
6. Ví dụ mô hình SEM trong thực tế
Giả sử bạn muốn nghiên cứu mối quan hệ giữa “chất lượng dịch vụ”, “sự hài lòng khách hàng” và “ý định mua lại”. Bạn xây dựng mô hình SEM trong SPSS hoặc AMOS gồm 3 biến tiềm ẩn và các biến quan sát tương ứng. Sau khi chạy mô hình, bạn sẽ biết:
- Chất lượng dịch vụ ảnh hưởng tích cực đến sự hài lòng.
- Sự hài lòng tác động mạnh đến ý định mua lại.
- Giá trị trung gian của sự hài lòng giữa chất lượng và ý định mua lại.
Đây là ví dụ mô hình SEM giúp minh họa rõ cách Structural Equation Modeling mô tả mối quan hệ nhân quả phức tạp và kiểm định độ phù hợp của mô hình với dữ liệu.
7. Kết luận
SEM Model là công cụ phân tích thống kê đa chiều giúp kiểm định và diễn giải các mối quan hệ nhân quả phức tạp trong nghiên cứu khoa học. Khi hiểu mô hình SEM là gì và biết cách áp dụng AMOS SEM hướng dẫn hay SPSS, bạn có thể xây dựng các mô hình dữ liệu chặt chẽ, chính xác và khoa học hơn.
Để thành thạo phân tích mô hình SEM, bạn nên bắt đầu từ việc học CFA, hiểu cấu trúc của các biến quan sát và tiềm ẩn, sau đó sử dụng phần mềm SPSS hoặc AMOS để mô phỏng và kiểm định. Việc nắm vững Structural Equation Modeling sẽ giúp bạn tiến xa trong lĩnh vực Xử lý số liệu và phân tích thống kê.
Cách chạy thống kê mô tả trong SPSS: Hướng dẫn chi tiết và cách đọc kết quả từng chỉ số
Cách chạy thống kê mô tả trong SPSS là bước đầu tiên và quan trọng trong quá trình phân tích dữ liệu. Thống kê mô tả giúp người dùng hiểu rõ đặc điểm tổng quan của tập dữ liệu, từ đó hỗ trợ việc ra quyết định và kiểm định các giả thuyết trong nghiên cứu. Bài viết dưới đây của Xử lý số liệu sẽ hướng dẫn bạn từng bước thực hiện và diễn giải kết quả một cách dễ hiểu, kèm theo ví dụ thực tế trên phần mềm SPSS.
1. Thống kê mô tả là gì?
Trước khi học cách chạy thống kê mô tả trong SPSS, bạn cần hiểu khái niệm cơ bản. Thống kê mô tả là phương pháp tổng hợp và trình bày dữ liệu giúp cung cấp cái nhìn tổng quan về các đặc điểm quan trọng của tập dữ liệu. Các chỉ số phổ biến bao gồm:
- Giá trị trung bình (Mean)
- Giá trị nhỏ nhất (Minimum)
- Giá trị lớn nhất (Maximum)
- Độ lệch chuẩn (Standard Deviation)
- Độ lệch (Skewness)
- Độ nhọn (Kurtosis)
- Sai số chuẩn (S.E. Mean)
Những chỉ số này cho phép nhà nghiên cứu đánh giá xu hướng, mức độ phân tán và hình dạng của phân phối dữ liệu. Việc hiểu rõ các chỉ số thống kê mô tả là nền tảng để bạn có thể diễn giải dữ liệu chính xác hơn.
2. Chuẩn bị dữ liệu để chạy thống kê mô tả trong SPSS

Để thực hành cách chạy thống kê mô tả trong SPSS, bạn cần có file dữ liệu định dạng .sav. Bạn có thể tải ví dụ dữ liệu mẫu từ xulysolieu.info để thực hành.
Sau khi mở file dữ liệu, mỗi cột đại diện cho một biến quan sát, còn mỗi dòng là một đối tượng khảo sát. Ví dụ: biến QUYETDINH1, QUYETDINH2, QUYETDINH3 phản ánh mức độ đồng ý của người trả lời với các phát biểu trong bảng hỏi Likert 5 mức.
3. Cách chạy thống kê mô tả trong SPSS – Hướng dẫn chi tiết
Bước 1: Trên thanh menu chính, chọn Analyze → Descriptive Statistics → Descriptives.
Bước 2: Chọn các biến cần thực hiện thống kê mô tả và đưa sang ô bên phải. Các biến được chọn sẽ là những biến bạn muốn mô tả dữ liệu.
Bước 3: Nhấn OK để chạy. SPSS sẽ hiển thị bảng kết quả thống kê mô tả trong cửa sổ Output.
Đây là thao tác cơ bản nhất của cách chạy thống kê mô tả trong SPSS. Dù đơn giản, nhưng đây là bước bắt buộc để hiểu được dữ liệu trước khi tiến hành các phân tích phức tạp hơn như hồi quy, phân tích nhân tố, hay kiểm định giả thuyết.
4. Cách đọc và diễn giải kết quả thống kê mô tả trong SPSS
Bảng kết quả thống kê mô tả trong SPSS sẽ bao gồm các cột sau:
- N: Số lượng mẫu hợp lệ. Ví dụ, N = 200 nghĩa là có 200 người tham gia khảo sát hợp lệ.
- Minimum: Giá trị nhỏ nhất của biến. Nếu biến QUYETDINH3 có minimum = 2, điều đó nghĩa là không có ai chọn mức 1 trong thang đo.
- Maximum: Giá trị lớn nhất. Nếu maximum = 5, có ít nhất một người chọn mức cao nhất trên thang Likert.
- Mean: Giá trị trung bình của biến. Ví dụ mean = 3.45 nghĩa là người trả lời có xu hướng đánh giá trên mức trung bình (vì mức trung bình là 3).
- Std. Deviation: Độ lệch chuẩn, thể hiện mức độ dao động của dữ liệu quanh giá trị trung bình.
Khi diễn giải kết quả thống kê mô tả, độ lệch chuẩn là một chỉ số quan trọng. Độ lệch chuẩn càng lớn chứng tỏ dữ liệu phân tán rộng, ý kiến của người trả lời khác nhau nhiều. Ngược lại, độ lệch chuẩn nhỏ nghĩa là câu trả lời của họ khá đồng nhất.
Ví dụ mô tả dữ liệu SPSS
Giả sử bạn có hai tập dữ liệu:
- Tập 1: (-1, 0, 1)
- Tập 2: (-100, 0, 100)
Cả hai tập đều có giá trị trung bình bằng 0. Tuy nhiên, độ lệch chuẩn của tập 2 lớn hơn rất nhiều, vì các giá trị dao động xa khỏi trung bình. Đây là ví dụ điển hình giúp bạn hiểu rõ hơn về ý nghĩa của độ lệch chuẩn trong cách chạy thống kê mô tả trong SPSS.
5. Một số lưu ý khi mô tả dữ liệu trong SPSS
- Nên kiểm tra dữ liệu bị thiếu (Missing Values) trước khi chạy thống kê.
- Không nên chỉ dựa vào giá trị trung bình để đánh giá, hãy xem thêm độ lệch chuẩn và khoảng giá trị (min – max).
- Đối với dữ liệu định tính, sử dụng tần suất (Frequencies) thay vì Descriptives để mô tả.
6. Kết luận
Qua bài viết này, bạn đã nắm rõ cách chạy thống kê mô tả trong SPSS cũng như hiểu ý nghĩa của từng chỉ số. Việc thực hiện thống kê mô tả là bước nền tảng trong phân tích dữ liệu, giúp bạn xác định xu hướng, phạm vi và mức độ biến động của các biến trong nghiên cứu.
Để luyện tập thêm, bạn có thể truy cập xulysolieu.info để tải dữ liệu mẫu và xem thêm hướng dẫn mô tả dữ liệu trong SPSS kèm ví dụ chi tiết. Khi đã thành thạo, bạn sẽ dễ dàng áp dụng cách chạy thống kê mô tả trong SPSS cho mọi dự án phân tích thực tế.
Phân tích tương quan là gì? Cách thực hiện phân tích tương quan Pearson trong SPSS
Phân tích tương quan là gì? Đây là kỹ thuật thống kê được dùng để đo lường và đánh giá mối quan hệ giữa các biến trong một tập dữ liệu. Cụ thể, nó cho biết mức độ và chiều hướng của mối liên hệ tuyến tính giữa hai biến định lượng. Khi muốn hiểu xem hai yếu tố có di chuyển cùng chiều hay ngược chiều, phân tích tương quan là bước đầu tiên mà các nhà nghiên cứu dữ liệu cần thực hiện.
1. Khái niệm cơ bản: Phân tích tương quan là gì?
Về mặt lý thuyết, phân tích tương quan là gì có thể hiểu đơn giản là việc định lượng hóa mối liên hệ giữa hai biến số. Hệ số này được biểu diễn bằng một con số duy nhất gọi là hệ số tương quan (correlation coefficient), ký hiệu là r.
Hệ số tương quan là gì? Đây là giá trị thể hiện mức độ chặt chẽ giữa hai biến định lượng, có thể dao động trong khoảng từ −1 đến 1:
- r → 1: mối tương quan dương mạnh (hai biến tăng/giảm cùng chiều).
- r → −1: mối tương quan âm mạnh (hai biến biến động ngược chiều).
- r → 0: không có tương quan tuyến tính đáng kể.
Khi r = 1, các điểm dữ liệu sẽ nằm trên một đường thẳng dốc lên hoàn hảo. Ngược lại, r = 0 cho thấy không có mối liên hệ tuyến tính nào giữa hai biến, mặc dù có thể tồn tại mối liên hệ phi tuyến.
2. Tương quan Pearson là gì?
Tương quan Pearson là phương pháp phổ biến nhất dùng trong phân tích tương quan. Hệ số này được gọi là hệ số tương quan Pearson (Pearson’s correlation coefficient) – công cụ đánh giá mức độ tuyến tính giữa hai biến định lượng. Khi dữ liệu chứa biến định tính hoặc biến nhị phân, thì không nên sử dụng tương quan Pearson mà thay bằng phương pháp khác như Spearman hoặc Kendall.
Giá trị của hệ số tương quan Pearson được tính dựa trên công thức:
r = Cov(X, Y) / (σX * σY)
Trong đó:
- Cov(X, Y): hiệp phương sai giữa hai biến X và Y.
- σX, σY: độ lệch chuẩn của từng biến.
Như vậy, để hiểu sâu phân tích tương quan là gì, bạn cần nắm rõ cách tính và diễn giải hệ số tương quan Pearson trong SPSS.
3. Cách thực hiện phân tích tương quan trong SPSS
Cách chạy phân tích tương quan trong SPSS rất đơn giản. Dưới đây là hướng dẫn chi tiết do xulysolieu.info biên soạn, giúp bạn áp dụng dễ dàng:
- Vào menu Analyze → Correlate → Bivariate….
- Chọn các biến muốn phân tích trong ô Variables.
- Tick chọn Pearson và Two-tailed để kiểm định hai phía.
- Nhấn OK để chạy phân tích tương quan.
Kết quả sẽ hiển thị trong bảng Correlations, gồm các cột:
- Pearson Correlation (r): hệ số tương quan Pearson.
- Sig. (2-tailed): giá trị sig (p-value) để kiểm định ý nghĩa thống kê.
- N: kích thước mẫu.
4. Cách đọc kết quả phân tích tương quan trong SPSS
Trong phân tích tương quan, có hai loại mối quan hệ cần quan tâm:
- Tương quan giữa biến phụ thuộc và biến độc lập: thể hiện mức độ tác động tiềm năng. Nếu sig < 0.05, tức là có mối tương quan tuyến tính đáng kể.
- Tương quan giữa các biến độc lập với nhau: nhằm phát hiện khả năng đa cộng tuyến. Nếu |r| > 0.7, có thể hai biến chứa thông tin trùng lặp.
Theo Andy Field (2009), ta có thể đánh giá độ mạnh của mối tương quan như sau:
- |r| < 0.1: rất yếu
- |r| < 0.3: yếu
- |r| < 0.5: trung bình
- |r| ≥ 0.5: mạnh
Đây là các quy ước giúp xác định mức độ liên hệ giữa các biến trong phân tích tương quan.
5. Ý nghĩa kiểm định trong phân tích tương quan
Khi SPSS hiển thị kết quả, bạn sẽ thấy ký hiệu và trong bảng:
- : mối tương quan có ý nghĩa ở mức tin cậy 99% (p < 0.01).
- : mối tương quan có ý nghĩa ở mức tin cậy 95% (p < 0.05).
Điều này giúp nhà phân tích xác định được đâu là mối quan hệ thật sự đáng tin cậy giữa các biến.
6. Ví dụ phân tích tương quan thực tế

Giả sử bạn muốn kiểm tra mối quan hệ giữa các biến như “Mức độ hài lòng của sinh viên” và “Chất lượng giảng dạy”. Sau khi chạy phân tích tương quan Pearson trong SPSS, kết quả cho thấy:
r = 0.68, Sig. (2-tailed) = 0.000, N = 200
Diễn giải:
- r = 0.68 → mối tương quan dương mạnh.
- Sig < 0.05 → mối quan hệ có ý nghĩa thống kê.
Như vậy, có thể kết luận rằng khi chất lượng giảng dạy tăng, mức độ hài lòng của sinh viên cũng tăng tương ứng. Đây là ví dụ điển hình giúp hiểu rõ phân tích tương quan là gì trong ứng dụng thực tế.
7. Ứng dụng và lưu ý khi phân tích tương quan
- Ứng dụng: được dùng phổ biến trong nghiên cứu hành vi, phân tích dữ liệu doanh nghiệp, giáo dục và y học.
- Lưu ý:
- Phân tích tương quan chỉ phản ánh mối liên hệ, không khẳng định nhân quả.
- Nếu biến không tuân theo phân phối chuẩn, nên dùng Spearman thay Pearson.
- Kết hợp phân tích tương quan với kiểm định đa cộng tuyến (VIF) trong hồi quy để đánh giá chính xác hơn.
8. Tổng kết
Như vậy, phân tích tương quan là gì – đó là bước cơ bản nhưng quan trọng trong thống kê, giúp bạn phát hiện và đánh giá mối quan hệ giữa các biến trong dữ liệu. Thông qua tương quan Pearson, bạn có thể xác định hướng và độ mạnh của liên hệ, kiểm định ý nghĩa thống kê và chuẩn bị cơ sở cho phân tích hồi quy.
Để thực hành thành thạo, bạn có thể tham khảo tài liệu chi tiết và ví dụ minh họa tại xulysolieu.info của đội ngũ Xử lý số liệu – nơi tổng hợp các bài hướng dẫn SPSS chuyên sâu, dễ hiểu và ứng dụng trực tiếp vào công việc nghiên cứu dữ liệu.
Skewness là gì? Cách tính và diễn giải độ lệch trong thống kê mô tả
Skewness là gì? Skewness hay còn gọi là độ lệch trong thống kê, là chỉ số cho biết mức độ bất đối xứng của một phân phối dữ liệu so với phân phối chuẩn. Khi dữ liệu có hình chuông hoàn toàn đối xứng, ta nói phân phối đó có skewness = 0. Ngược lại, nếu dữ liệu bị lệch về bên trái hoặc bên phải, skewness sẽ mang giá trị âm hoặc dương.
Trong Xử lý số liệu, việc hiểu rõ skewness là gì giúp người phân tích đánh giá hình dạng của dữ liệu, từ đó chọn mô hình thống kê phù hợp hơn và giải thích ý nghĩa kết quả một cách chính xác.
1. Khái niệm Skewness trong thống kê
Skewness là thước đo cho biết dữ liệu có xu hướng tập trung về phía nào so với trung bình. Khi phân phối bị “kéo dài” về một phía, ta nói dữ liệu bị lệch. Cụ thể:
- Skewness dương (Positive Skewness): Đuôi phân phối kéo dài về bên phải. Giá trị trung bình lớn hơn trung vị. Ví dụ điển hình là phân phối thu nhập, khi một số cá nhân có thu nhập rất cao làm kéo trung bình lên.
- Skewness âm (Negative Skewness): Đuôi phân phối kéo dài về bên trái. Giá trị trung bình nhỏ hơn trung vị. Ví dụ: điểm kiểm tra khi hầu hết học sinh đạt điểm cao, chỉ vài người điểm thấp.
- Skewness bằng 0: Phân phối đối xứng, trung bình bằng trung vị và mode, như phân phối chuẩn.
Trong thực hành, khi bạn biết độ lệch trong thống kê là dương hay âm, bạn sẽ hiểu rõ hơn về xu hướng dữ liệu của mình có đang tập trung nhiều ở giá trị thấp hay cao.
2. Công thức tính Skewness

Skewness có thể được tính theo nhiều cách, trong đó phổ biến nhất là hệ số độ lệch Pearson. Có hai biến thể chính của công thức tính skewness:
Công thức 1: SK1 = (Giá trị trung bình - Yếu vị) / Độ lệch chuẩn Công thức 2: SK2 = 3 * (Giá trị trung bình - Trung vị) / Độ lệch chuẩn
Trong đó:
- SK1: Hệ số độ lệch thứ nhất của Pearson (Pearson’s Mode Skewness)
- SK2: Hệ số độ lệch thứ hai của Pearson (Pearson’s Median Skewness)
- Độ lệch chuẩn: Đo mức độ phân tán của dữ liệu quanh trung bình
Nếu bạn đang học cách tính skewness trong SPSS, phần mềm sẽ tự động hiển thị giá trị này trong bảng Descriptive Statistics. Việc quan trọng là biết cách đọc kết quả: nếu giá trị skewness nằm trong khoảng -1 đến +1, dữ liệu được coi là khá đối xứng. Nếu vượt quá khoảng này, dữ liệu bị lệch mạnh.
3. Cách đọc Skewness trong SPSS
Khi chạy mô tả trong SPSS (Analyze → Descriptive Statistics → Descriptives), bạn có thể chọn thêm tùy chọn Skewness và Kurtosis. SPSS sẽ hiển thị giá trị skewness kèm theo sai số chuẩn của nó.
Cách đọc skewness trong SPSS:
- Nếu skewness ≈ 0: Dữ liệu đối xứng, gần phân phối chuẩn.
- Nếu skewness > 0: Dữ liệu lệch phải, nhiều giá trị nhỏ, một vài giá trị lớn kéo trung bình lên.
- Nếu skewness < 0: Dữ liệu lệch trái, nhiều giá trị lớn, vài giá trị nhỏ kéo trung bình xuống.
Để dễ nhớ, bạn có thể xem biểu đồ histogram trong SPSS để trực quan hóa: đuôi kéo dài bên nào, skewness sẽ cùng hướng đó.
4. Ví dụ Skewness trong thực tế
Giả sử bạn khảo sát mức thu nhập hàng tháng của 100 người. Kết quả thu được: đa số nằm trong khoảng 10–20 triệu, nhưng có một số cá nhân thu nhập trên 100 triệu. Khi đó, phân phối thu nhập bị lệch phải, nên skewness > 0.
Ngược lại, nếu bạn khảo sát điểm thi và hầu hết học sinh đạt điểm cao (8–10), chỉ vài người điểm thấp (1–3), phân phối sẽ lệch trái, skewness < 0.
Như vậy, qua ví dụ skewness, ta thấy chỉ số này giúp nhà nghiên cứu nhận diện được dạng của phân phối mà không cần nhìn biểu đồ. Điều này đặc biệt hữu ích khi làm việc với dữ liệu lớn trong SPSS hoặc Excel.
5. Ý nghĩa Skewness trong phân phối chuẩn
Hiểu được ý nghĩa skewness trong phân phối chuẩn rất quan trọng vì nhiều mô hình thống kê giả định dữ liệu tuân theo phân phối chuẩn. Nếu dữ liệu có skewness khác 0 quá lớn, các giả định này có thể bị vi phạm.
Ví dụ, trong phân tích hồi quy hoặc kiểm định giả thuyết, dữ liệu lệch nhiều có thể khiến kết quả không còn chính xác. Do đó, trước khi phân tích, các nhà thống kê thường kiểm tra skewness để xem có cần biến đổi dữ liệu (log, square root, hay Box-Cox transformation) nhằm làm giảm độ lệch hay không.
Xử lý số liệu khuyến nghị rằng khi skewness nằm trong khoảng từ -0.5 đến +0.5 thì phân phối có thể xem là chuẩn; nếu vượt ra ngoài khoảng này, cần xem xét điều chỉnh.
6. Tầm quan trọng của Skewness trong phân tích dữ liệu
Biết skewness là gì giúp bạn hiểu sâu hơn về bản chất dữ liệu. Chỉ số này không chỉ mang ý nghĩa mô tả mà còn ảnh hưởng đến độ tin cậy của các phân tích suy luận.
Trong phân tích tài chính, độ lệch trong thống kê thường được dùng để đánh giá rủi ro đầu tư. Nếu lợi nhuận của một cổ phiếu có skewness dương lớn, có nghĩa là khả năng có vài giá trị lợi nhuận cực cao nhưng phần lớn lợi nhuận thấp. Ngược lại, skewness âm thể hiện rủi ro mất mát lớn trong một số ít trường hợp.
7. Tổng kết
Tóm lại, skewness là gì không chỉ là câu hỏi về mặt định nghĩa, mà còn là yếu tố then chốt trong việc hiểu hình dạng và xu hướng của dữ liệu. Biết cách tính skewness, đọc skewness trong SPSS, và diễn giải ý nghĩa skewness trong phân phối chuẩn sẽ giúp bạn đánh giá dữ liệu một cách chuyên nghiệp và chính xác hơn.
Nếu bạn đang học thống kê hoặc làm việc trong lĩnh vực Xử lý số liệu, hãy luôn kiểm tra skewness cùng với kurtosis để hiểu rõ hơn về đặc trưng của tập dữ liệu trước khi ra quyết định hoặc chạy mô hình dự đoán.
Bài viết được biên soạn độc quyền bởi xulysolieu.info, chuyên trang phân tích dữ liệu và xử lý số liệu học thuật.
Logistic Regression SPSS: Hướng dẫn chạy hồi quy logistic và đọc kết quả chi tiết
Bài hướng dẫn này tập trung vào logistic regression spss: hiểu hồi quy logistic là gì, cách kiểm định giả định, cách chạy logistic regression trong SPSS, và diễn giải kết quả logistic regression spss theo chuẩn báo cáo nghiên cứu. Tài liệu và hỗ trợ thực hành có tại xulysolieu.info – dịch vụ Xử lý số liệu.
1) Hồi quy logistic là gì?
Hồi quy logistic nhị phân dự đoán xác suất một biến phụ thuộc nhị phân (0/1) xảy ra dựa trên một hay nhiều biến độc lập định lượng hoặc định tính. Với logistic regression spss, đầu ra chính là logit của xác suất, odds và odds ratio. Nếu biến phụ thuộc là đếm, dùng Poisson; nếu đa lớp >2, dùng multinomial. Khi triển khai logistic regression spss, bạn làm việc với hàm liên kết logit nên hệ số hồi quy diễn giải theo log-odds/odds ratio.
2) Giả định cần kiểm tra trước khi chạy logistic regression SPSS
- DV nhị phân: 0/1 rõ ràng. Đây là tiền đề của logistic regression spss.
- IV dạng liên tục hoặc phân loại: được phép dùng cả hai trong logistic regression spss.
- Độc lập quan sát: không lặp lại đo trên cùng cá thể, phù hợp khuôn khổ logistic regression spss.
- Tuyến tính giữa biến liên tục và logit: kiểm bằng Box–Tidwell trong logistic regression spss; nếu vi phạm, xem xét biến đổi hoặc phân đoạn.
- Không đa cộng tuyến nghiêm trọng: kiểm tra hệ số tương quan cao; trong logistic regression spss có thể thăm dò qua ma trận tương quan hoặc chạy OLS phụ để xem VIF tham khảo.
- Không có outlier ảnh hưởng lớn: rà soát casewise residuals, leverage, Cook’s trong logistic regression spss.
Nếu vi phạm một số giả định, vẫn có giải pháp: biến đổi biến, phân loại, loại điểm ngoại lai hợp lý, hoặc chọn mô hình khác. Đây là thực tế thường gặp khi thao tác logistic regression spss.
3) Ví dụ logistic regression
Giả sử dự đoán “bệnh tim: có/không” theo tuổi, cân nặng, giới, VO2max. Đây là kịch bản chuẩn để minh họa toàn bộ quy trình logistic regression spss từ nhập dữ liệu, đặt mã, chạy lệnh đến báo cáo.
4) Chuẩn bị dữ liệu trong SPSS
- Mã hóa DV:
heart_disease(0 = không, 1 = có). Cách mã hóa nhất quán là điều kiện của logistic regression spss. - Biến liên tục:
age,weight,vo2maxđể dùng trực tiếp trong logistic regression spss. - Biến phân loại:
gender(0 = nữ, 1 = nam). Cần khai báo “Categorical…” đúng trong logistic regression spss để thiết lập nhóm tham chiếu.
5) Cách chạy logistic regression trong SPSS

- Vào Analyze > Regression > Binary Logistic… để mở hộp thoại logistic regression spss.
- Đưa
heart_diseasevào Dependent; đưaage,weight,gender,vo2maxvào Covariates theo chuẩn logistic regression spss. - Nhấn Categorical…, chuyển
gendersang “Categorical Covariates”, chọn Reference Category = First hoặc Last đúng theo mã hóa 0/1. Bước này quyết định cách SPSS tạo biến giả trong logistic regression spss. - Nhấn Options…, chọn:
- Hosmer–Lemeshow goodness-of-fit để kiểm độ phù hợp trong logistic regression spss.
- Classification plots, Casewise listing of residuals để xem phân loại và ngoại lệ trong logistic regression spss.
- CI for Exp(B) để lấy khoảng tin cậy odds ratio trong logistic regression spss.
- Giữ Method = Enter cho mô hình chuẩn logistic regression spss; nhấn OK.
6) Diễn giải kết quả logistic regression SPSS
6.1. Độ phù hợp mô hình
- Hosmer–Lemeshow test: p > 0.05 ngụ ý mô hình phù hợp dữ liệu, một tiêu chí căn bản khi đọc logistic regression spss.
- -2 Log Likelihood: càng nhỏ càng tốt; dùng để so sánh mô hình trong logistic regression spss.
- Cox & Snell R² và Nagelkerke R²: “pseudo R²”, báo cáo Nagelkerke R² vì có thể tiến gần 1. Đây là thước đo phần phương sai giải thích trong logistic regression spss.
6.2. Bảng phân loại (Classification Table)
Cho biết tỷ lệ dự báo đúng tổng thể (PAC), Sensitivity (TPR), Specificity (TNR), PPV, NPV với ngưỡng cắt mặc định 0.5. Khi tối ưu hiệu năng trong logistic regression spss, có thể thay đổi cut-off theo mục tiêu cân bằng nhạy/đặc hiệu hoặc chi phí sai lầm.
6.3. Bảng “Variables in the Equation”
- B: hệ số log-odds; S.E.: sai số chuẩn; Wald và Sig.: kiểm định ý nghĩa từng biến trong logistic regression spss.
- Exp(B): odds ratio; 95% CI cho Exp(B) là mấu chốt diễn giải trong logistic regression spss.
- Ví dụ diễn giải: Exp(B)=7.03 cho
gender(nam so với nữ) nghĩa là odds mắc bệnh tim của nam cao gấp 7.03 lần, nếu p<0.05 trong logistic regression spss.
7) Báo cáo kết quả theo chuẩn

Mẫu báo cáo gọn:
Mô hình logistic regression spss dự đoán bệnh tim theo tuổi, cân nặng, giới, VO2max có ý nghĩa chung (χ², p<0.001). Nagelkerke R²=0.33. Hosmer–Lemeshow p=0.41 cho thấy độ phù hợp chấp nhận được. Bảng phân loại đạt 78% PAC, Se=70%, Sp=83% tại cut-off 0.5. Về biến riêng lẻ, tuổi (B=0.04, p=0.003), giới nam (OR=7.03, p=0.021) và VO2max (OR=0.95, p=0.039) có ý nghĩa; cân nặng không có ý nghĩa (p=0.799).
Khi viết bài, nhắc rõ thước đo (OR, CI 95%), p-value, và pseudo-R² để hoàn thiện phần diễn giải kết quả logistic regression spss.
8) Thực hành tốt và bẫy thường gặp
- Mã hóa tham chiếu: xác định nhóm 0/1 nhất quán trước khi chạy logistic regression spss.
- Tuyến tính logit: kiểm Box–Tidwell cho biến liên tục trong logistic regression spss; nếu vi phạm, dùng spline hoặc phân loại bậc thang.
- Tương tác: thêm biến tương tác nếu có lý thuyết hỗ trợ; đánh giá qua Wald trong logistic regression spss.
- Thang đo khác nhau: cân nhắc chuẩn hóa để cải thiện ổn định ước lượng trong logistic regression spss.
- Class imbalance: nếu lớp dương hiếm, cân nhắc điều chỉnh cut-off, trọng số hoặc kỹ thuật lấy mẫu khi dùng logistic regression spss.
9) Câu hỏi nhanh
Hồi quy logistic là gì? Mô hình xác suất cho DV nhị phân. Trong logistic regression spss, hệ số diễn giải bằng odds ratio.
Cách chạy logistic regression trong SPSS? Analyze > Regression > Binary Logistic…; đặt DV, IV, khai báo categorical, chọn Hosmer–Lemeshow, CI cho Exp(B) và chạy. Đó là quy trình chuẩn logistic regression spss.
Diễn giải kết quả logistic regression spss? Kiểm Hosmer–Lemeshow, pseudo-R², bảng phân loại, và bảng hệ số với OR, CI, p-value.
Ví dụ logistic regression? Dự đoán bệnh tim bằng tuổi, cân nặng, giới, VO2max minh họa đầy đủ các bảng của logistic regression spss.
10) Tài nguyên và hỗ trợ
Để có template báo cáo, file dữ liệu thực hành, và checklist giả định cho logistic regression spss, xem xulysolieu.info. Khi cần đội ngũ triển khai phân tích, mô hình hóa và viết báo cáo logistic regression spss cho luận văn hay đề án doanh nghiệp, liên hệ dịch vụ Xử lý số liệu.
Bài tập hồi quy tuyến tính đơn biến: Lời giải chi tiết & Hướng dẫn thao tác
Bài tập hồi quy tuyến tính đơn biến là nền tảng quan trọng trong phân tích dữ liệu và nghiên cứu định lượng. Đây là dạng hồi quy cơ bản nhất giúp mô tả và dự đoán mối quan hệ giữa một biến độc lập (X) và một biến phụ thuộc (Y). Bài viết dưới đây do đội ngũ Xử lý số liệu tại xulysolieu.info biên soạn, cung cấp hướng dẫn chi tiết cách làm, lời giải hồi quy tuyến tính và hướng dẫn thao tác thực hành bằng SPSS.
1. Khái niệm và ý nghĩa của hồi quy tuyến tính đơn biến
Trước khi bắt đầu với bài tập hồi quy tuyến tính đơn biến, bạn cần hiểu bản chất của mô hình này. Hồi quy tuyến tính đơn biến là mô hình ước lượng mối quan hệ giữa hai biến: biến độc lập X (nguyên nhân) và biến phụ thuộc Y (kết quả). Công thức tổng quát:
Y = a + bX
- a: hệ số chặn (intercept) – giá trị Y khi X = 0
- b: hệ số góc (slope) – mức thay đổi trung bình của Y khi X tăng 1 đơn vị
Hiểu rõ công thức này giúp bạn dễ dàng giải thích kết quả trong bài tập hồi quy trong SPSS hay khi đọc bảng kết quả trên phần mềm thống kê.
2. Quy trình giải bài tập hồi quy tuyến tính đơn biến
Để hoàn thành một bài tập hồi quy tuyến tính đơn biến, ta cần đi qua 4 bước cơ bản:
- Xác định biến: chọn 1 biến độc lập (X) và 1 biến phụ thuộc (Y).
- Nhập dữ liệu: nhập bộ số liệu khảo sát hoặc giả định vào phần mềm SPSS.
- Thực hiện hồi quy: vào
Analyze → Regression → Linear. - Đọc và diễn giải kết quả: dựa vào bảng Coefficients, ANOVA và Model Summary.
Đây là cấu trúc chung áp dụng cho mọi cách chạy hồi quy đơn biến và có thể mở rộng cho hồi quy bội sau này.
3. Ví dụ hồi quy tuyến tính: Thực hành chi tiết
Xét ví dụ hồi quy tuyến tính sau:
Giả sử ta muốn phân tích mối quan hệ giữa doanh số bán hàng (Y) và ngân sách quảng cáo (X). Dữ liệu thu được từ 10 cửa hàng như sau:
| Cửa hàng | Ngân sách quảng cáo (triệu đồng) | Doanh số (triệu đồng) |
|---|---|---|
| 1 | 10 | 25 |
| 2 | 12 | 28 |
| 3 | 15 | 35 |
| 4 | 18 | 40 |
| 5 | 20 | 45 |
| 6 | 25 | 50 |
| 7 | 28 | 53 |
| 8 | 30 | 58 |
| 9 | 35 | 63 |
| 10 | 40 | 70 |
Mục tiêu: Xây dựng phương trình hồi quy và diễn giải kết quả.
Bước 1: Nhập dữ liệu trong SPSS
Tạo hai biến: “QuangCao” (X) và “DoanhSo” (Y) trong Variable View. Sau đó nhập dữ liệu trên vào Data View. Đây là thao tác cơ bản trong giải bài tập hồi quy bằng SPSS.
Bước 2: Chạy mô hình hồi quy
Vào menu Analyze → Regression → Linear. Chọn:
- Dependent:
DoanhSo - Independent:
QuangCao
Nhấn OK để SPSS xuất ra kết quả phân tích.
Bước 3: Đọc kết quả
SPSS xuất ra ba bảng quan trọng trong bài tập hồi quy tuyến tính đơn biến:
Bảng Model Summary
R = 0.98, R2 = 0.96 → Mô hình giải thích được 96% sự biến thiên của doanh số.
Bảng ANOVA
Sig. = 0.000 < 0.05 → mô hình có ý nghĩa thống kê.
Bảng Coefficients
| Biến | B | Sig. |
|---|---|---|
| Hằng số | 10.5 | 0.001 |
| QuangCao | 1.5 | 0.000 |
Phương trình hồi quy: DoanhSo = 10.5 + 1.5 * QuangCao
Giải thích: Khi ngân sách quảng cáo tăng 1 triệu đồng, doanh số trung bình tăng 1.5 triệu đồng.
4. Diễn giải kết quả và nhận xét
Đây là bước quan trọng nhất trong mọi bài tập hồi quy tuyến tính đơn biến. Mô hình đạt yêu cầu khi:
- Hệ số R2 lớn (≥ 0.5), chứng tỏ mô hình giải thích tốt.
- Sig. < 0.05 ở bảng ANOVA → mô hình có ý nghĩa.
- Sig. của hệ số X < 0.05 → X tác động có ý nghĩa đến Y.
Trong ví dụ này, cả ba điều kiện đều đạt → mô hình phù hợp. Đây là lời giải hồi quy tuyến tính chuẩn mực, có thể trình bày trong báo cáo hoặc luận văn.
5. Cách chạy hồi quy đơn biến và kiểm định giả thuyết

Trong bài tập hồi quy tuyến tính đơn biến, cần nhớ trình tự kiểm định giả thuyết:
- Giả thuyết H0: hệ số b = 0 (X không ảnh hưởng Y)
- Giả thuyết H1: b ≠ 0 (X ảnh hưởng Y)
Dựa vào giá trị Sig. trong bảng Coefficients: nếu Sig. < 0.05 thì bác bỏ H0, chấp nhận H1. Khi đó biến X có tác động ý nghĩa đến biến Y. Quy tắc này áp dụng cho mọi bài tập hồi quy trong SPSS.
6. Những lỗi thường gặp khi giải bài tập hồi quy tuyến tính đơn biến
- Nhập nhầm biến độc lập và phụ thuộc.
- Không kiểm tra Sig. < 0.05 → kết luận sai mô hình.
- Hiểu nhầm R và R2.
- Không lưu ý đơn vị đo → sai diễn giải hệ số B.
Để tránh lỗi, hãy tham khảo hướng dẫn thao tác trực quan tại xulysolieu.info – nền tảng chuyên về giải bài tập hồi quy bằng SPSS và xử lý dữ liệu thực tế.
7. Mở rộng bài tập và luyện tập thêm
Hãy thử tự luyện thêm 3 dạng bài tập hồi quy tuyến tính đơn biến sau:
- Phân tích mối quan hệ giữa thu nhập và chi tiêu hộ gia đình.
- Phân tích giữa thời gian học và điểm thi cuối kỳ.
- Phân tích giữa giá quảng cáo và lượng truy cập website.
Mỗi bài tập đều có thể được chạy trên SPSS, Excel hoặc R. Nhưng SPSS được ưa chuộng vì thao tác nhanh, dễ đọc và cho biểu đồ trực quan.
8. Tổng kết
Bài tập hồi quy tuyến tính đơn biến là bước khởi đầu để hiểu các mô hình phân tích phức tạp hơn. Khi bạn làm chủ được cách chạy hồi quy đơn biến và hiểu cách diễn giải hệ số, việc xử lý dữ liệu và viết báo cáo sẽ trở nên dễ dàng. Hãy thực hành thường xuyên để quen với quy trình từ nhập liệu đến diễn giải kết quả. Nếu bạn cần hỗ trợ chuyên sâu về thống kê hoặc muốn được hướng dẫn theo mô hình thực tế, hãy truy cập xulysolieu.info để được đội ngũ Xử lý số liệu hỗ trợ.
Phương pháp chọn mẫu phi xác suất: Định nghĩa, ưu nhược điểm và cách áp dụng hiệu quả
Phương pháp chọn mẫu phi xác suất là kỹ thuật lấy mẫu phổ biến trong nghiên cứu xã hội, marketing và hành vi người tiêu dùng. Khác với các phương pháp ngẫu nhiên, kỹ thuật này không yêu cầu xác suất chọn mẫu bằng nhau cho mọi phần tử trong tổng thể. Bài viết từ xulysolieu.info – Xử lý số liệu sẽ giúp bạn hiểu rõ khái niệm, các loại phương pháp chọn mẫu phi xác suất, cùng cách áp dụng và đánh giá ưu – nhược điểm cụ thể.
1. Phương pháp chọn mẫu phi xác suất là gì?
Phương pháp chọn mẫu phi xác suất là gì? Đây là cách chọn mẫu mà xác suất để một phần tử trong tổng thể được chọn không thể xác định hoặc không bằng nhau. Việc chọn mẫu phụ thuộc vào sự tiện lợi, phán đoán của người nghiên cứu hoặc đặc điểm tiếp cận của đối tượng.
Phương pháp chọn mẫu phi xác suất thường được sử dụng khi:
- Tổng thể nghiên cứu quá lớn hoặc không thể xác định khung mẫu đầy đủ.
- Cần kết quả nhanh, chi phí thấp.
- Mục tiêu nghiên cứu mang tính khám phá, định tính hoặc mô tả sơ bộ.
Theo xulysolieu.info, đây là nhóm phương pháp thường được dùng trong giai đoạn khảo sát ban đầu, nghiên cứu thị trường, hoặc khi đối tượng nghiên cứu khó tiếp cận.
2. Các loại phương pháp chọn mẫu phi xác suất phổ biến
2.1. Chọn mẫu thuận tiện (Convenience Sampling)
Chọn mẫu thuận tiện là dạng cơ bản nhất của phương pháp chọn mẫu phi xác suất. Nhà nghiên cứu lựa chọn những người dễ tiếp cận hoặc sẵn có xung quanh mình. Ví dụ, phỏng vấn người quen, đồng nghiệp, hoặc người đi ngang qua khu vực khảo sát.
Ưu điểm: Nhanh, tiết kiệm, dễ triển khai.
Nhược điểm: Mẫu không đại diện cho tổng thể, dễ sai lệch do thiên vị cá nhân.
Ví dụ thực tế: Một nhóm sinh viên chọn khảo sát bạn học cùng trường vì thuận tiện về thời gian và địa điểm. Dù dữ liệu thu được nhanh, nhưng không phản ánh toàn bộ sinh viên trong khu vực.
2.2. Chọn mẫu hạn ngạch (Quota Sampling)
Chọn mẫu hạn ngạch là kỹ thuật chia tổng thể thành các nhóm phụ (ví dụ: giới tính, độ tuổi, nghề nghiệp), rồi lấy mẫu thuận tiện trong từng nhóm cho đến khi đạt đủ số lượng (hạn ngạch) đã định.
Ví dụ: Cần khảo sát 100 người gồm 50 nam, 50 nữ. Nhà nghiên cứu phỏng vấn ngẫu nhiên những người gặp được cho đến khi đủ số lượng mỗi nhóm.
Ưu điểm: Giúp cân bằng tỷ lệ nhóm; nhanh hơn chọn mẫu ngẫu nhiên phân tầng.
Nhược điểm: Không đảm bảo tính ngẫu nhiên trong từng nhóm, có thể sai lệch khi chọn người tham gia.
Trong các bài hướng dẫn tại xulysolieu.info, chọn mẫu hạn ngạch thường được khuyến nghị cho nghiên cứu thị trường sơ bộ.
2.3. Chọn mẫu phán đoán (Judgement Sampling / Purposive Sampling)
Chọn mẫu phán đoán hay còn gọi là chọn mẫu có mục đích, được áp dụng khi nhà nghiên cứu dựa vào kinh nghiệm hoặc chuyên môn để chọn các đối tượng có đặc điểm phù hợp với mục tiêu nghiên cứu. Đây là phương pháp phổ biến trong điều tra chuyên sâu, phỏng vấn chuyên gia hoặc nghiên cứu xã hội học.
Ví dụ: Khi nghiên cứu về ảnh hưởng của ô nhiễm không khí, nhà nghiên cứu có thể chọn những người sống gần khu công nghiệp để phỏng vấn.
Ưu điểm: Tập trung vào nhóm có thông tin giá trị, tiết kiệm thời gian.
Nhược điểm: Dễ sai lệch chủ quan, khó tổng quát hóa kết quả.
2.4. Chọn mẫu quả bóng tuyết (Snowball Sampling)
Chọn mẫu quả bóng tuyết thường dùng cho các nhóm đối tượng hiếm hoặc khó tiếp cận. Nhà nghiên cứu bắt đầu từ một mẫu nhỏ ban đầu, sau đó nhờ họ giới thiệu thêm những người có đặc điểm tương tự để mở rộng mẫu – giống như một quả cầu tuyết lăn dần lớn lên.
Ví dụ: Nghiên cứu về người nghiện game online hoặc người nhập cư trái phép – hai nhóm khó tiếp cận trực tiếp.
Ưu điểm: Hiệu quả cho nghiên cứu xã hội học hoặc nhóm nhỏ đặc biệt.
Nhược điểm: Mẫu bị phụ thuộc vào mạng lưới giới thiệu, không kiểm soát được tính ngẫu nhiên.
Phương pháp chọn mẫu phi xác suất này được hướng dẫn chi tiết trong các khóa học xử lý dữ liệu chuyên sâu của xulysolieu.info.
2.5. Lấy mẫu tự lựa chọn (Self-selection Sampling)
Lấy mẫu tự lựa chọn là hình thức người tham gia tự nguyện tham gia khảo sát. Phương pháp này thường dùng trong khảo sát online hoặc nghiên cứu tâm lý học hành vi người tiêu dùng.
Ví dụ: Bảng khảo sát trực tuyến mời người dùng điền ý kiến về sản phẩm mới.
Ưu điểm: Dễ triển khai, tiết kiệm chi phí, phù hợp nghiên cứu trực tuyến.
Nhược điểm: Dễ sai lệch do chỉ có những người quan tâm chủ động tham gia.
2.6. Chọn mẫu chuyên gia (Expert Sampling)
Phương pháp chọn mẫu phi xác suất này tập trung vào việc chọn những người có chuyên môn trong lĩnh vực nghiên cứu. Dạng này thường được dùng trong nghiên cứu chính sách, kinh tế, hoặc kỹ thuật.
Ví dụ: Mời nhóm chuyên gia công nghệ thảo luận về xu hướng trí tuệ nhân tạo.
Ưu điểm: Độ tin cậy cao nhờ ý kiến chuyên sâu.
Nhược điểm: Khó tập hợp nhóm chuyên gia phù hợp, yêu cầu người phân tích có kiến thức chuyên môn cao.
2.7. Nhóm quan tâm (Focus Group)
Đây là dạng phỏng vấn nhóm nhỏ (10–20 người) có cùng đặc điểm tiêu dùng hoặc hành vi. Mục tiêu là thảo luận sâu về sản phẩm hoặc dịch vụ cụ thể để thu thập ý kiến chi tiết.
Ưu điểm: Cung cấp insight chất lượng cao, phù hợp cho nghiên cứu định tính.
Nhược điểm: Tốn công tổ chức, kết quả khó lượng hóa.
3. So sánh mẫu phi xác suất và xác suất

| Tiêu chí | Mẫu phi xác suất | Mẫu xác suất |
|---|---|---|
| Cách chọn mẫu | Dựa vào sự thuận tiện hoặc phán đoán của người nghiên cứu | Dựa trên xác suất ngẫu nhiên, mỗi phần tử có cơ hội bằng nhau |
| Khả năng đại diện | Thấp, khó khái quát kết quả | Cao, kết quả có thể suy rộng cho tổng thể |
| Chi phí – thời gian | Thấp, nhanh triển khai | Cao, cần nhiều nguồn lực |
| Ứng dụng | Nghiên cứu khám phá, sơ bộ, định tính | Nghiên cứu mô tả, phân tích định lượng lớn |
4. Ưu nhược điểm của phương pháp chọn mẫu phi xác suất
Ưu điểm chọn mẫu phi xác suất:
- Triển khai nhanh, tiết kiệm chi phí.
- Phù hợp với đối tượng khó tiếp cận.
- Có thể thu được insight chuyên sâu trong nghiên cứu định tính.
Nhược điểm chọn mẫu phi xác suất:
- Tính đại diện thấp, độ tin cậy hạn chế.
- Dễ chịu ảnh hưởng bởi thiên vị cá nhân của nhà nghiên cứu.
- Không thể ước lượng sai số chọn mẫu chính xác.
Vì vậy, phương pháp chọn mẫu phi xác suất phù hợp nhất cho nghiên cứu khám phá, điều tra hành vi, hoặc giai đoạn tiền nghiên cứu – nơi mục tiêu chính là hiểu sâu hơn về hiện tượng, chứ không phải suy luận thống kê toàn bộ tổng thể.
5. Khi nào nên sử dụng phương pháp chọn mẫu phi xác suất?
Theo hướng dẫn của xulysolieu.info, bạn nên sử dụng phương pháp chọn mẫu phi xác suất khi:
- Không có khung chọn mẫu đầy đủ.
- Đối tượng nghiên cứu hiếm, khó tiếp cận (như nhóm bệnh nhân, nghệ sĩ, chuyên gia).
- Thời gian, nguồn lực nghiên cứu hạn chế.
- Mục tiêu là tìm hiểu xu hướng, khám phá hiện tượng, chứ không cần khái quát hóa.
6. Kết luận
Phương pháp chọn mẫu phi xác suất là công cụ quan trọng trong nghiên cứu ứng dụng, đặc biệt ở giai đoạn khám phá hoặc phân tích định tính. Dù có hạn chế về tính đại diện, nhưng các kỹ thuật như chọn mẫu thuận tiện, chọn mẫu phán đoán, chọn mẫu hạn ngạch, hay chọn mẫu quả bóng tuyết vẫn mang lại giá trị lớn nếu được áp dụng đúng bối cảnh. Nắm rõ ưu nhược điểm chọn mẫu phi xác suất giúp bạn chọn chiến lược lấy mẫu phù hợp với mục tiêu nghiên cứu.
Để tìm hiểu sâu hơn về kỹ thuật chọn mẫu và thực hành phân tích dữ liệu, truy cập xulysolieu.info – nền tảng chuyên cung cấp khóa học và dịch vụ Xử lý số liệu cho luận văn và dự án nghiên cứu chuyên nghiệp.
Width là gì trong SPSS? Hướng dẫn cách dùng và điều chỉnh Width khi xử lý dữ liệu
Width là gì trong ngữ cảnh SPSS? Đây là số lượng ký tự tối đa mà một biến có thể hiển thị và lưu trữ. Với Numeric, width tính tổng chữ số hiển thị (phần nguyên + dấu thập phân + dấu âm nếu có). Với String, width là độ dài chuỗi ký tự. Nắm rõ width là gì giúp bạn tránh lỗi “cụt chữ”, bảng kết quả méo và file dữ liệu phình to không cần thiết. Bài viết này đi thẳng vào thực hành: vị trí cột Width trong Variable View, nguyên tắc đặt width, cách kiểm thử và các lỗi thường gặp khi thiết lập dữ liệu SPSS. Nội dung tham chiếu theo kinh nghiệm triển khai tại xulysolieu.info của đội ngũ Xử lý số liệu.
1) Khái niệm cốt lõi: width là gì và ảnh hưởng đến phân tích ra sao?
- Width là gì: tham số xác định độ rộng dữ liệu cho từng biến.
- Numeric: width = tổng chữ số hiển thị, chịu ảnh hưởng bởi Decimals.
- String: width = trần độ dài chuỗi.
- Tác động: width nhỏ → cắt bớt ký tự; width quá lớn → tệp nặng, thao tác chậm.
Quy tắc nền tảng khi nghĩ về width là gì: đặt “đủ dùng” theo dữ liệu dài nhất dự kiến. Đừng phóng đại. Cũng đừng để mặc định rồi hy vọng mọi thứ sẽ ổn.
2) Cột Width trong Variable View nằm ở đâu và dùng thế nào?
Mở Variable View bạn sẽ thấy các cột: Name, Type, Width, Decimals, Label, Values, Missing, Measure. Để chỉnh width, bấm vào cột Width trong Variable View của biến tương ứng và nhập giá trị mới. Đây là thao tác căn bản trong nhập liệu SPSS cơ bản.
Khi đã hiểu width là gì, bạn sẽ luôn kiểm tra song song với Decimals (Numeric) và chiều dài chuỗi dự kiến (String) trước khi nhập dữ liệu hàng loạt.
3) Quy tắc thực hành đặt width cho Numeric
- Thang Likert 1–5/7/9: width = 1, Decimals = 0.
- Số nguyên nhỏ (0–999): width ≈ 3–4, Decimals = 0.
- Có phần thập phân: tính tổng chữ số cần hiển thị. Ví dụ 1234.56 → tối thiểu 7 ký tự (4 số + dấu chấm + 2 thập phân) → width ≈ 7–8, Decimals = 2.
- Tiền tệ lớn: dự trù biên độ tối đa rồi cộng phần thập phân để xác định width.
Sai lầm phổ biến: tăng Decimals nhưng giữ nguyên width. Hiểu rõ width là gì sẽ nhắc bạn luôn “cộng đủ” số chỗ cho phần thập phân và ký hiệu.
4) Quy tắc thực hành đặt width cho String
- Tên, chức danh ngắn: width ≈ 30–40.
- Phòng ban/bộ phận: width ≈ 20–30.
- Ghi chú ngắn: width ≈ 100–200 khi thật sự cần.
Nếu chuỗi dài hơn width, SPSS sẽ cắt đuôi. Hiểu width là gì giúp bạn nhận ra ngay nguyên nhân bảng dữ liệu “cụt chữ”. Cách khắc phục duy nhất: tăng width cho biến đó.
5) Liên hệ giữa Width, Type, Decimals và Measure
- Type quyết định cách diễn giải dữ liệu. Numeric bị ràng bởi Decimals; String ràng bởi độ dài chuỗi.
- Decimals chỉ tác động tới Numeric, nhưng làm thay đổi width tối thiểu cần hiển thị.
- Measure không đổi width nhưng ảnh hưởng tới cách mô tả và thống kê.
Khi đã trả lời xong “width là gì”, bước tiếp theo là “width cần bao nhiêu” dựa trên Type và Decimals.
6) Checklist nhanh theo dạng câu hỏi khảo sát
- Định tính một lựa chọn (giới tính, độ tuổi nhóm…): ưu tiên Numeric mã hóa 1–n → width = 1–2, Decimals = 0.
- Định lượng một giá trị (chiều cao, cân nặng…): Numeric, tính đủ phần nguyên + thập phân → xác định width phù hợp.
- Likert 5/7/9 mức: Numeric 1–5/7/9 → width = 1, Decimals = 0.
- Câu mở: String. Xác định độ dài tối đa hợp lý, đặt width vừa đủ.
Việc hiểu width là gì giúp bạn cấu hình chính xác ngay ở Variable View, từ đó các bước mô tả, tương quan, EFA, hồi quy hiển thị sạch và đúng.
7) Cách chỉnh width trong SPSS: quy trình 4 bước
- Xác định giá trị dài nhất dự kiến cho từng biến.
- Chọn Type rồi xác định Decimals (nếu Numeric).
- Tính width cần thiết: phần nguyên + dấu thập phân + phần thập phân (+ dấu âm nếu có).
- Kiểm thử vài dòng “dài nhất” ở Data View. Nếu bị cắt → tăng width; nếu dư quá nhiều → giảm để gọn file.
Mỗi lần bạn tự hỏi “width là gì với biến này?”, hãy quay lại quy trình trên để ra con số tối ưu.
8) Lỗi thường gặp và cách khắc phục
- Cụt chữ ở String: width quá nhỏ. Tăng width trong Variable View.
- Số hiển thị không đủ: tăng Decimals mà quên tăng width. Tính lại tổng chữ số cần hiển thị.
- File nặng bất thường: đặt width cực lớn cho nhiều biến String. Giảm width về mức “đủ dùng”.
- Bảng/biểu đồ méo nhãn: nhãn dài nhưng width không đủ, tạm thời tăng width trước khi xuất báo cáo.
Nhận diện nhanh nhờ câu hỏi gốc “width là gì và tôi đã đặt nó đúng chưa?”.
9) Hỏi đáp nhanh
Q: Width spss là gì?
A: Cách SPSS giới hạn số ký tự hiển thị và lưu trữ cho một biến. Hiểu đúng width là gì giúp bạn tránh lỗi hiển thị và tối ưu dung lượng.
Q: Giảm width có mất dữ liệu không?
A: Có thể, nếu chiều dài thực tế vượt quá width mới. Hãy tự nhắc “width là gì” trước khi cắt giảm.
Q: Tăng width có an toàn?
A: Có. Tăng width chỉ mở rộng sức chứa, không làm mất dữ liệu hiện có.
Q: Cách chỉnh width trong SPSS ở đâu?
A: Trong Variable View, chỉnh trực tiếp ở cột Width trong Variable View cho từng biến.
10) Mẫu quyết định nhanh theo bối cảnh
- Biến mã hóa 1–9: width = 1.
- Biến mã 10–99: width = 2.
- Giá trị tối đa 12345.6: width tối thiểu = 7, Decimals = 1.
- Chuỗi tối đa ~25 ký tự: width = 30 để có biên an toàn.
Mỗi dòng trên đều bắt đầu từ việc trả lời chính xác width là gì với dữ liệu của bạn.
11) Kết luận và nguồn tham khảo thực hành
Khi bạn hiểu rõ width là gì, bạn sẽ thiết lập biến đúng ngay từ đầu, tránh lỗi hiển thị, tối ưu kích thước file và giữ cho pipeline từ mô tả đến hồi quy hoạt động mượt. Hãy đưa câu hỏi “width là gì ở biến này?” vào checklist nhập liệu. Nếu cần khung khai báo biến tối ưu sẵn (Name, Type, Width, Decimals, Label, Values, Missing), bạn có thể tham khảo hướng dẫn thực hành tại xulysolieu.info của đội ngũ Xử lý số liệu.
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy SPSS – SPSS 10
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-spss/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
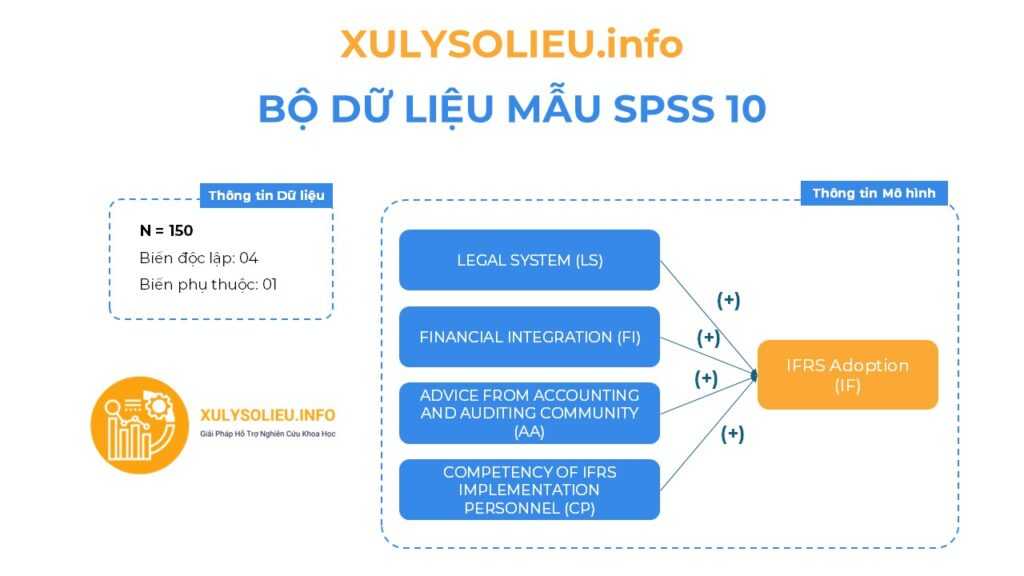
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 150
- Mô hình nghiên cứu bao gồm 05 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (sử dụng thang đo Likert 5)
- Biến độc lập: 04
+ LEGAL SYSTEM (LS): 5 items
+ FINANCIAL INTEGRATION (FI): 5 items
+ ADVICE FROM ACCOUNTING AND AUDITING COMMUNITY (AA): 5 items
+ COMPETENCY OF IFRS IMPLEMENTATION PERSONNEL (CP): 5 items - Biến phụ thuộc: 01
+ IFRS Adoption (IF): 4 items
Thông tin các biến định tính
- Gender
- Years of professional work
- Job position
- Qualifications
- Bank type
2. Chi tiết kết quả kiểm định Dữ Liệu mẫu
- Các file bạn sẽ nhận được: File dữ liệu excel + File Word kết quả + File xử lý phần mềm tương ứng
- Link xem trước kết quả dữ liệu: Tại đây!
Giá gốc: 299k VND- Giá ưu đãi: 168k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI
Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-spss/
Bộ Dữ Liệu Mẫu (Data Mẫu) Xử Lý và Chạy SPSS – SPSS 09
Để đảm bảo tính minh bạch và hỗ trợ tốt nhất cho khách hàng, chúng tôi xin lưu ý một số ghi chú đối với các bộ dữ liệu mẫu như sau:
A. Dữ Liệu Mẫu Từ Các Nghiên Cứu Thực Tế
- Các bộ dữ liệu mẫu được xây dựng dựa trên mô hình và giả thuyết tác động, đã qua kiểm định với các chỉ số kết quả chi tiết để khách hàng dễ dàng tham khảo và sử dụng.
B.Lựa chọn tùy chỉnh đối với Dữ Liệu Mẫu
- Các bộ dữ liệu mẫu không có tùy chọn thay đổi hoặc điều chỉnh theo yêu cầu riêng của từng khách hàng đối với từng bộ Dữ Liệu Mẫu. Nếu bạn đang có nhu cầu tìm một bộ dữ liệu riêng biệt hoặc chỉnh sửa chi tiết theo nhu cầu cụ thể, vui lòng tham khảo option Tùy Chỉnh VIP từ Xulysolieu.info.
C.Yêu cầu bộ dữ liệu theo thang đo của bạn
- Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu riêng, hoặc cần hỗ trợ thu thập câu trả lời cho Form câu hỏi (GG Form, Microsoft form…) vui lòng truy cập vào phần Dịch vụ tại Xulysolieu.info để biết thêm thông tin và nhận hỗ trợ từ đội ngũ chuyên gia.
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-spss/
1. Tổng quan về mô hình: Các nhân tố và các biến quan sát trong Dữ Liệu mẫu
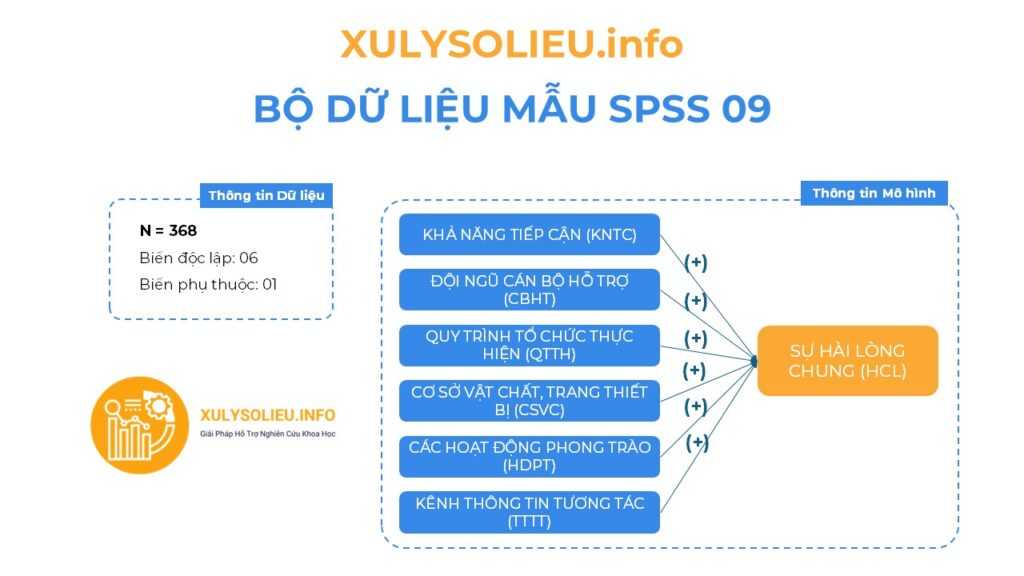
- Bộ dữ liệu mẫu với cỡ mẫu hợp lệ (N): 368
- Mô hình nghiên cứu bao gồm 07 biến
- Tất cả các mối quan hệ tương quan thuận chiều (+)
Thông tin các biến định lượng (sử dụng thang đo Likert 5)
- Biến độc lập: 06
+ KHẢ NĂNG TIẾP CẬN (KNTC) : 4 items
+ ĐỘI NGŨ CÁN BỘ HỖ TRỢ (CBHT): 6 items
+ QUY TRÌNH TỔ CHỨC THỰC HIỆN (QTTH): 7 items
+ CƠ SỞ VẬT CHẤT, TRANG THIẾT BỊ (CSVC): 5 items
+ CÁC HOẠT ĐỘNG PHONG TRÀO (HDPT): 4 items
+ KÊNH THÔNG TIN TƯƠNG TÁC (TTTT): 5 items - Biến phụ thuộc: 01
+ SỰ HÀI LÒNG CHUNG (HCL): 4 items
Thông tin các biến định tính
- Giới tính
- Chuyên ngành
2. Chi tiết kết quả kiểm định Dữ Liệu mẫu
- Các file bạn sẽ nhận được: File dữ liệu excel + File Word kết quả + File xử lý phần mềm tương ứng
- Link xem trước kết quả dữ liệu: Tại đây!
Giá gốc: 299k VND- Giá ưu đãi: 168k VND
3. Thanh toán nhận Dữ Liệu mẫu
Bước 1: Thực hiện thanh toán cho Dữ liệu mẫu
– Ngân hàng Quân đội (MB)
– Số tài khoản: 0878968468
– Tên tài khoản: LE VAN HOANG VI

Bước 2: Gửi chứng từ xác nhận qua Zalo

Bước 3: Nhận file qua email
Trong trường hợp bạn muốn tùy chỉnh bộ dữ liệu theo câu hỏi có sẵn hoặc cần hỗ trợ xây dựng dữ liệu theo mô hình hoặc cần coaching chạy phần mềm. Vui lòng xem thêm tại:
xulysolieu.info/dich-vu-spss/